增强材料对塑料性能的影响

各种增强材料各有不同的特性，可以根据制品的性能要求选择适当的增强材料来配制塑料。但是，增强材料对配制后塑料性能的改性作用的大小是由多方面因素综合影响而定的，不是单纯的选择某一种增强材料就可完全决定该塑料的性能的。

1.选用的树脂和增强材料品种及其匹配性

树脂在增强塑料中是决定塑料基本特性的基体，同时又起粘结剂作用，纤维是塑料中的填料，同时起骨架的作用，有较高的刚性但呈脆性，两者各有本身的优缺点，当两者复合后可达到性能互补，纤维可承受外界较大的载荷应力，树脂通过与纤维界面上的剪切应力支撑纤维，并可将外界载荷传递分布至各部位。由于不同树脂和纤维的性能不同，两者结合性的强弱也不同，因此不同品种的树脂和纤维材料，以及两者亲和性强弱（即匹配性）都会直接影响增强塑料的性能。

2.增强材料的品种

如前所述，增强材料的品种很多，其性能不等，各有不同用途。几种常用纤维的性能见表12-3。玻璃纤维及其织物的用途见表12-4。

表12-3 几种常用纤维的性能

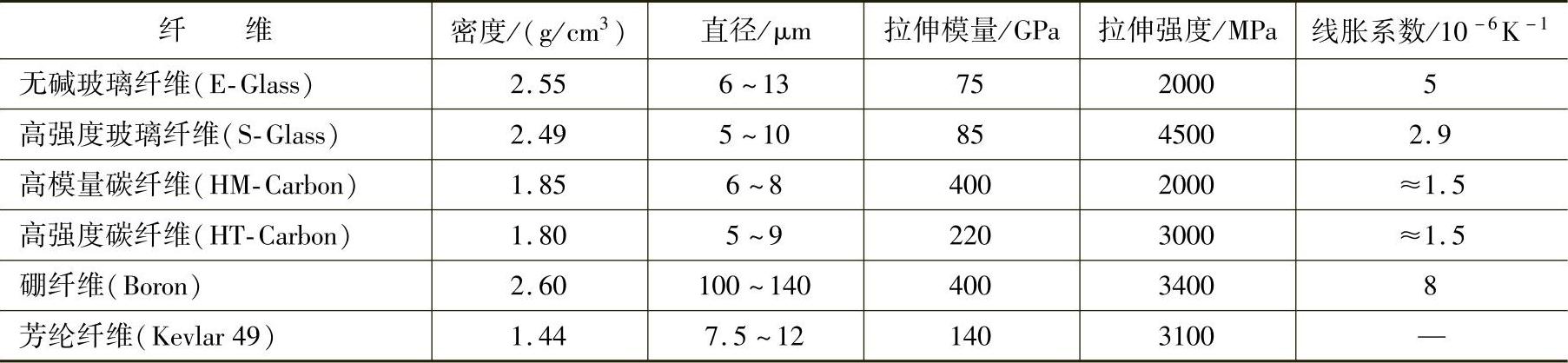
表12-4 玻璃纤维及其织物的用途

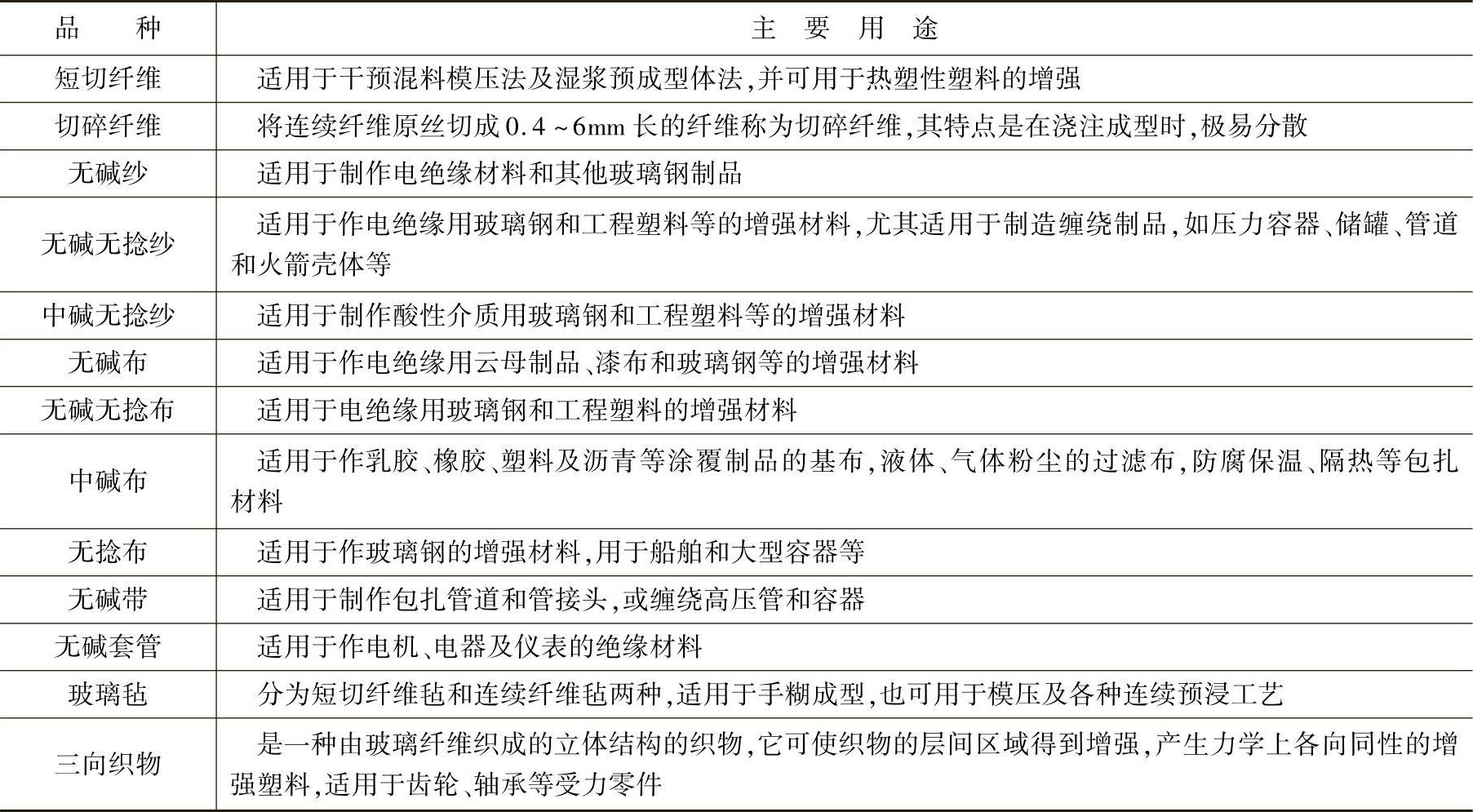
另外，各个品种的纤维还可分为不同纤径、长度、长径比和股数（支数）等许多规格，它们对塑料的增强作用的影响也各不相同，如长纤维增强塑料的强度、模量、韧性和耐热性都优于短切纤维增强塑料，但成型加工性相对较差。

3.增强材料的含量

塑料中增强材料的含量对塑料性能有很大的影响。通常，增强材料含量高，则强度和刚度增大，但脆性也增大，同时热膨胀系数、成型收缩率和吸水率也随之下降，且成型加工性也变差。

目前，常用的增强塑料中增强材料含量约为10%～80%（体积分数）。

塑料中增强材料含量有体积组分和质量组分两种表示方法，两者关系式为

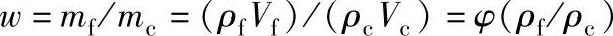
式中，w是纤维在塑料中质量组分；m_f是纤维的质量；m_c是塑料的质量；ρ_f、ρ_c分别是纤维和塑料的密度；V_f、V_c分别是纤维和塑料体积；φ是纤维在塑料中体积组分。当ρ_f>ρ_c时，则φ>w；反之，则φ<w。

增强塑料中纤维及基体的体积和质量组分对增强塑料的拉伸强度、刚性等性能有直接关系，且可用数学关系表示。

（1）长纤维塑料的性能与体积组分的关系式常用混合定律来表示材料的拉伸强度、拉伸弹性模量、密度、热性能和电性能等性能与体积组分的关系。

1）单向长纤维塑料纵向拉伸模量与体积组分关系式为

E_cl=E_fφf+E_mφ_m

式中，E_cl、E_f、E_m分别是增强塑料、纤维和树脂的拉伸弹性模量；φ_f、φ_m是纤维和树脂的体积组分，φ_f+φ_m=1。

2）单向长纤维塑料密度与体积组分的关系式为

ρc=ρ_fφ_f+ρ_mφ_m

式中，ρ_c、ρ_f、ρ_m分别是增强塑料、纤维和树脂的密度。

3）单向长纤维增强塑料拉伸强度与体积组分的关系式为

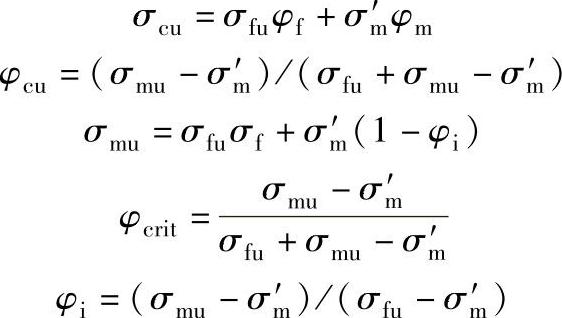
式中，σ_cu、σ_fu、σ_m′、σ_mu分别是长纤维增强塑料的纵向强度（估算值），长纤维的拉伸强度、长纤维增强塑料中纤维断裂时基体的拉伸强度和增强塑料基体的强度，σ_m′<σ_mu；φ_f、φ_m、φ_crit、φ_i分别是增强塑料长纤维的体积组分，增强塑料基体的体积组分，增强塑料长纤维的体积组分的临界值，即纤维体积组分超过此值时σ_cu>σ_mu，获得增强效果的长纤维的体积组分的最小值。

实际上，单向长纤维的最大体积组分φ_max是0.8。增强塑料的长纤维的体积组分应在φ_i～φ_max之间。按混合定律可较精确计算出增强塑料的纵向弹性模量。但单向长纤维增强塑料的实际纵向强度，是按混合定律计算强度的65%左右，故用σ_cu式计算后还须进一步修正。

例：聚醚醚酮（PEEK）被用30%体积组分的单向长碳纤维增强。PEEK（1300kg/m³）在纤维断裂应变下测得拉伸强度σ′_m=0.058GPa。PEEK树脂的拉伸强度σ_mu=0.093GPa，模量E_m=3.8GPa。碳纤维（1800kg/m³）的拉伸强度σ_fu=2.1GPa，模量E_f=400GPa。试求：①增强塑料的密度、纵向的模量和强度；②在纵向拉伸时纤维所承受的载荷；③纤维的临界体积含量和最低含量。

解：①由混合定律

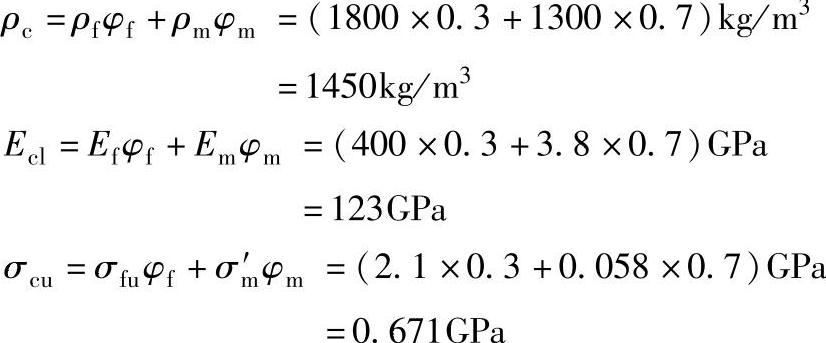
若用PEEK的σ_m=0.093GPa代入得σ_cu=0.695GPa，比计算结果略大。

②纤维承载作用力

F_f=σ_fA_f=E_fε_fφ_fV_c

同理，可得增强塑料所承受作用力

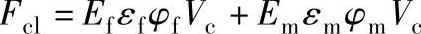
因此

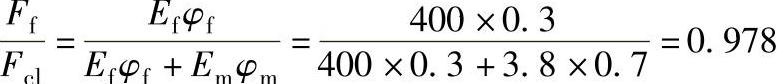
③纤维临界体积含量和最低含量

（2）非纵向性能 当单向长纤维增强塑料受拉伸时，如果拉伸方向偏离纵向，则力学性能下降，偏离越大，拉伸强度及弹性模量下降越大。垂直纤维的横向弹性模量E_ct和抗拉力F_ct比纵向的E_cl和F_cl小得多。此时，E、σ与φ的关系式也不同，预测横向模量E_ct的计算式有如下两种方法：

1）Brintrup计算法，计算式为

E_ct=E_fE_m′/（φ_fE_m′+φ_mE_f）

式中，E_ct、E_f、E′_m分别是增强塑料横向弹性模量，纤维弹性模量及纤维断裂时树脂的弹性模量；φ_f、φ_m是纤维和树脂在塑料中体积组分。

2）Nielsen法，计算式为

E_ct=E_m（1+ABφ_f）/（1-Bφ_fψ）

式中，填充单向长纤维时A=0.5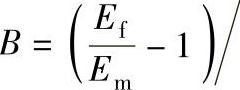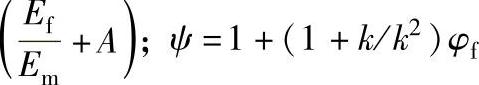；，对于纤维随机分布时k=0.85，六边形格式k=0.907，正方形格式k=0.785。

计算应用举例如下：

例：300mm宽、10mm厚的层合板，每层均为沿着载荷方向的单向长纤维。上层为环氧树脂和玻璃纤维复合，EP/玻璃纤维中纤维体积含量φ_f1=0.6，厚度t₁=3mm。中间层为EP/碳纤维，其中φ_f2=0.33，t₂=4mm。底层为EP/芳纶，其φ_f3=0.4，t₃=3mm。EP在纤维断裂时的拉伸强度σ_e′_p=0.07GPa，拉伸模量E_ep=6GPa；玻璃纤维的拉伸强度σ_glass=2.1GPa，拉伸模量E_glass=73GPa；碳纤维的拉伸强度σ_carb=2.8GPa，拉伸模量E_carb=240GPa；芳纶纤维的拉伸强度σ_kev=3.0GPa，拉伸模量E_kev=130GPa。求此层合板的承载能力。

解：用上述E与σ的混合定律式计算各层纵向E_cl和σ_cl，即可得

EP/玻璃纤维：E_cl=46.2GPa；σ_cl=1.29GPa

EP/碳纤维：E_cl=83.2GPa；σ_cl=0.97GPa

EP/芳纶纤维：E_cl=55.6GPa；σ_cl=1.24GPa

各层在载荷方向有相同的应变，每层的应力为

(www.xing528.com)

当σ_glass=σcl=1.29GPa时，可计算得

σ_carb=2.32GPa>σ_cl，碳纤维已断裂；

σ_kev=1.55GPa>σ_cl，芳纶纤维已断。

也就是说，在玻璃纤维断裂前，其余两层的纤维已经断裂。

当σ_kev=σ_cl=1.24GPa时，计算得

σ_glass=1.03GPa<σ_cl，玻璃纤维未断；

σ_carb=1.86GPa>σ_cl，碳纤维已断裂。

当σ_carb=σ_cl=0.97GPa时，计算得

σ_glass=0.54GPa<σ_cl，玻璃纤维未断；

σ_kev=0.65GPa<σ_cl，芳纶纤维也未断。

因此，在碳纤维层达到强度条件时，此层合板达到极限负载值。有

F_max=[0.97×10³×300×4+（0.65+0.54）×10³×300×3]kN=2.24MN

当碳纤维层失效时，由玻璃纤维层和芳纶纤维层承载，尚有的承载能力为

F_glass，kev=[1.24×10³×300×3+1.03×10³×300×3]kN=2.04MN

（3）短纤维增强塑料力学性能与纤维组分的关系短纤维增强塑料中纤维的主要几何参数有直径（一般为7～100μm）、长度（3～5mm）和纤维长径比对增强塑料承载能力有很大的影响。另外，短切纤维在塑料的分布状态可分为单向及随机分布两种形式，其承载的负荷能力也不一样，因此短纤维增强料的拉伸强度及弹性模量计算方法也不同。

短切纤维受拉应力时纤维会变长，当最大拉应力σ_fmax达到纤维拉伸断裂强度σ_fu时，纤维长度就达到临界长度l_c；如果在增强塑料中使短纤维的平均应力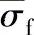能接近σ_fmax，则纤维的长度l必须大于临界长度l_c；如果选用的短纤维长度等于临界长度，则纤维平均应力仅为连续长纤维承载应力的1/2。

随机取向短切纤维增强塑料强度和模量比连续纤维增强料小得多，一般为连续纤维增强料的20%～25%，且短纤维最大体积组分也是连续纤维的1/2，φ_max是0.4。有关计算式如下：

1）单向短切纤维增强塑料（l>l_t），计算公式为

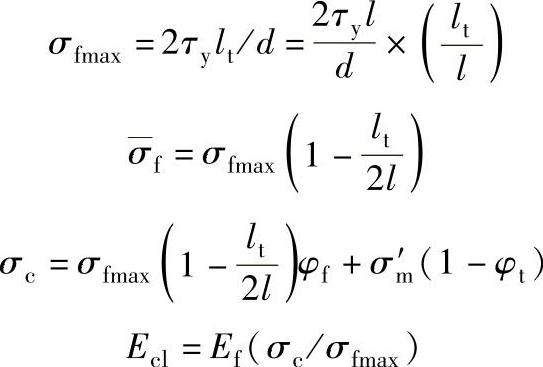
式中，σ_fmax、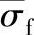、σ_c分别是纤维承受的最大应力、纤维承载的平均应力和纤维纵向承载应力；E_cl是塑料纵向弹性模量；l、l_t、l_c分别是纤维长度、纤维受σ_fmax应力时转变长度和纤维受拉伸断裂强度σ_fu时临界长度，l_t=σ_fmaxd/（2τ_y），l_c=σ_fud/（2τ_y）；d是纤维直径；τ_y是纤维变力滑动时纤维与基体截面上存在的剪切转变应力。

2）随机取向短切纤维增强塑料，计算公式为

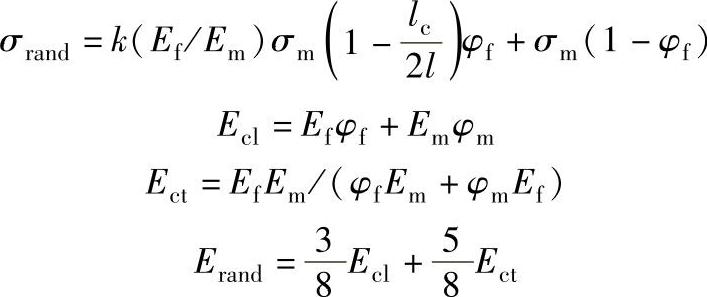
式中，σ_rand、E_rand分别是随机取向短切纤维增强塑料拉伸强度及拉伸弹性模量；E_cl、E_ct分别是纵向和横向弹性模量；k是系数。

计算举例如下：

例一：单向短玻璃纤维组分φ_f=0.3增强的聚酯。玻璃纤维直径d=18μm，长l=3mm。转变长度l_t与l之比为0.3。玻璃纤维的模量E_f=75GPa。界面的剪切强度τ_y=4MPa。聚酯强度σ_m=60MPa，作为基体σ_m′=50MPa。试求：①增强塑料中纤维的平均承载应力；②增强塑料的强度和模量。

解：①l>l_t，有

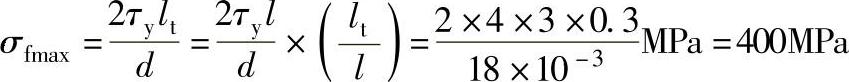
短纤维的承载平均应力为

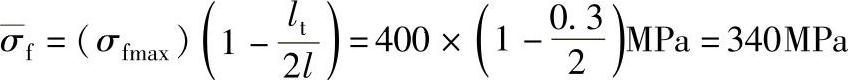
②增强塑料纵向承载能力为

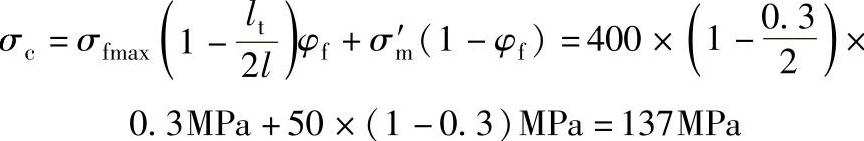
增强塑料纵向弹性模量为

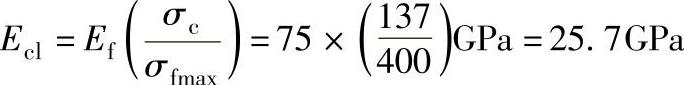
例二：随机取向短玻璃纤维增强PA66塑料，有玻璃纤维含量φ_f=0.2。玻璃纤维长l=5mm，直径d=10μm，E_f=75GPa，σ_f=2GPa，界面剪切强度τ_y=4MPa。PA66的E_m=2.8GPa，σ_m=0.07GPa。试求该增强塑料的强度和模量。

解：短纤维的临界长度为

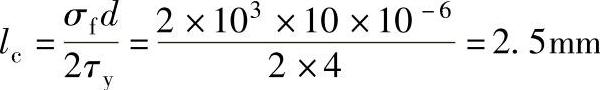
随机取向短纤维增强塑料承载能力（l>l_c）为

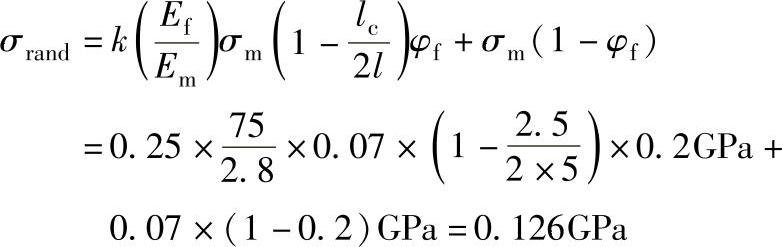
纵向和横向弹性模量为

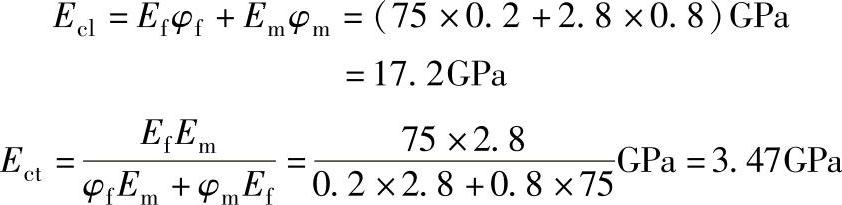
随机取向短纤维增强塑料的拉伸弹性模量

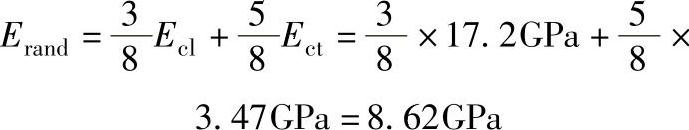
4.增强材料的表面处理

为了提高增强材料（纤维）与树脂的结合性，在纤维表面必须涂覆表面处理剂（主要包括浸润剂、偶联剂及其他助剂等）。其中，偶联剂对纤维及树脂都有良好的柔和性，可在纤维与树脂间形成一个良好的粘合界面，提高纤维与树脂粘结强度及剪切强度。同时，还可提高增强塑料的防水、绝缘、耐磨等性能，因此纤维表面处理时选用的处理剂必须与纤维和树脂相容匹配，且要保证浸润质量。两者都直接影响增强塑料的性能。

5.增强材料的取向性

多数增强纤维具有较高的强度与刚性，但呈脆性，且它们在塑料中分布状态也会直接影响增强塑料的密度、强度、刚性及热性能和电性能。塑料沿纤维分布的纵向和横向的性能差别很大，具有明显的取向性。如热固性增强塑料常用模压成型或层压成型加工制品，其玻璃纤维在垂直模压压力平面上纤维呈多种取向排列，有长纤维单向取向、长纤维相互垂直双向取向和短纤维随机排列取向等。

热塑性玻璃纤维增强塑料常用注射成型加工制品，其中纤维取向有沿注射方向单向取向，也有单向和双向组成混合取向，在滚塑成型时常呈随机取向。

纤维在塑料中的取向性对塑料各项性能都有较大的影响，如力学性能、热性能、电性能、线胀系数和成型收缩率等，两向的指标值差异很大。取向性越强，物性差异越大。

增强纤维在塑料中的取向程度还与成型工艺、工艺条件、树脂的成型特性、纤维含量、长度、长径比、树脂取向性、树脂与纤维匹配性等许多因素有关，因此即使是同一品种的增强塑料，在不同情况下加工的制品其性能也不同。

6.不同成型工艺对塑料性能影响较大

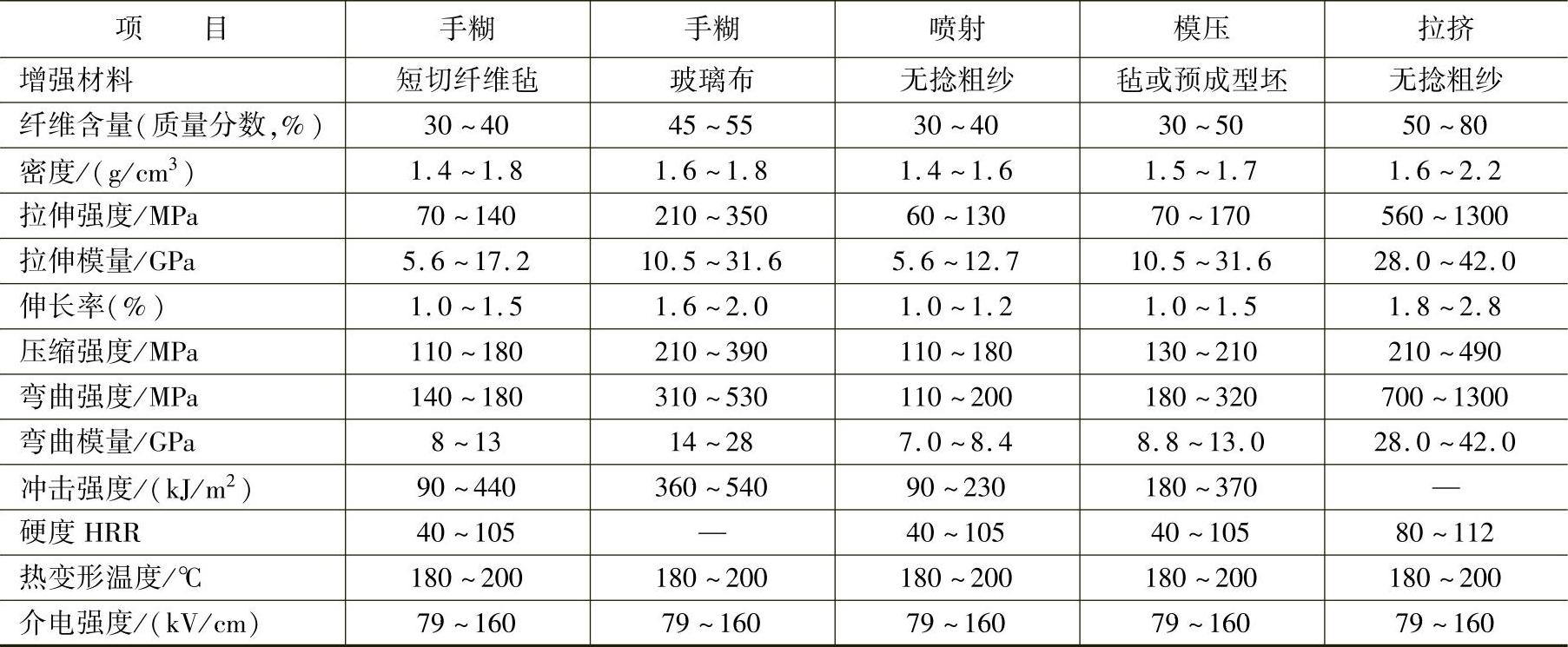
不同成型工艺应选用不同形式的增强材料，在制品中增强材料的含量及加工中纤维损伤程度也不同。因此同一种塑料采用不同成型工艺加工的制品，其物性也不相同。采用不同工艺成型的聚酯玻璃钢制品的性能见表12-5。

表12-5 采用不同工艺成型的聚酯玻璃钢制品的性能

综上所述，在按制品性能及成型工艺选择增强塑料品种时，应选择综合效果较好的品种。