如何优化商品包装中的缓冲击性能？

许多商品在装卸和运输过程中经常会受到翻滚、碰撞、抛掷、跌落等冲击负载的作用，同时在交通工具起动、制动、晃动、颠簸时也会受到激振冲击和脉动冲击负载的作用。为了防止损坏商品，常采用各种缓冲包装措施。这些包装材料及包装物必须具有足够的抗振缓冲性能。不同的包装结构件可能会受到不同的冲击负载。外包装物易受到高速冲击负载的冲击破坏，所以包装物结构设计及选用材料必须具有足够的抗冲击性能，而内包装结构在结构设计及选材时则注重于吸收激振的能量（冲量负载），使其能起到缓冲支撑的作用，如图6-38所示。本节主要介绍缓冲支撑结构的性能及计算。

图6-38中的K及C表示缓冲材料的粘弹性。当商品受冲击时假定外包装箱是刚性且无回弹的，则商品在缓冲支撑保护下发生很大的动态位移，而缓冲支撑也发生较大的变形量，且与动态负载值成正比。此时，只要变形量及应变在缓冲材料的弹性极限变形量范围内，则商品就不会受到直接冲击，缓冲支撑不失弹性，能起到吸收冲击能量和缓冲保护的作用。

图6-38 商品线性防冲保护模拟

如果材料的应变与负载呈线性关系，则需要对缓冲支撑材料进行静态压缩试验，以获取σ-ε关系曲线，进而按下列步骤进行缓冲性能计算：

1）最大动态位移量

2）冲击作用下的加速度

3）跌落时动态负载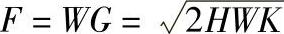

4）跌落时瞬时速度

5）单自由度低阻尼振动系统时商品的固有率

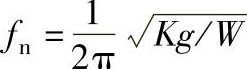
如果缓冲材料用泡沫塑料，则应力及应变呈非线性关系，由于常用的结构泡沫塑料刚性高，受冲击时呈脆性断裂，抗冲击性差，且与材料厚度、质量大小有关，动态应力大，则抗冲击性越差，所以要对材料进行动态压缩试验，通常采用落球（重锤）试验方法，获取各种材料不同厚度时峰值加速度a与静态应力σ_a关系曲线，如图6-39所示。(www.xing528.com)

其计算步骤如下：

1）求静态应力σ_a

σ_a=W/A

2）求缓冲垫厚度。用峰值加速度破坏性试验确定峰值加速度a查a-σ_a曲线即可求得缓冲垫厚度h。

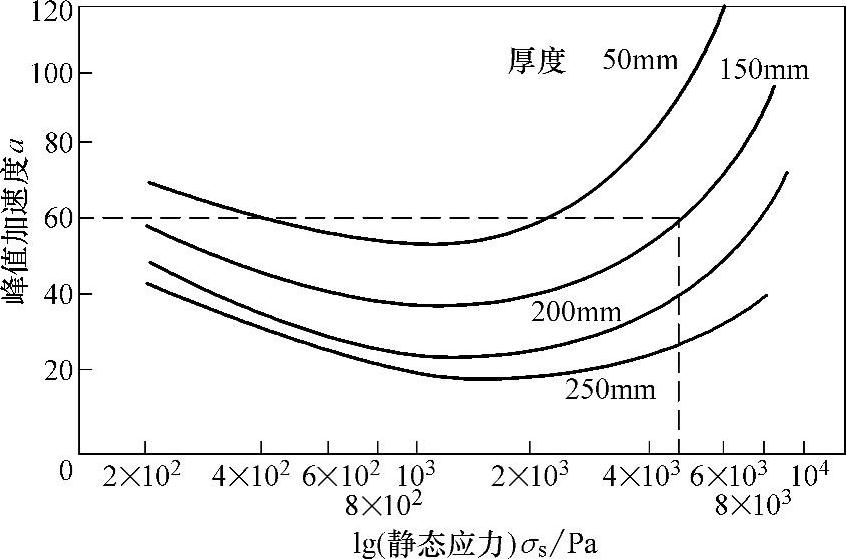
图6-39 聚氨酯泡沫缓冲材料（密度62.8kg/m³，24℃）的峰值加速度G与静态应力σ_s关系曲线（重锤高度为0.76m）

3）求动态冲击应力σ_d

σ_d=Wa/A

或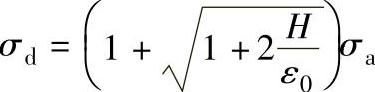

式中，W是商品的重力或重锤的重力（N）；A是缓冲垫支撑面积（m²）；H是落锤（商品）跌落高度（m）；ε₀是静载应变。

非线性缓冲性能计算方法还有缓冲系数法及不同跌落高度/缓冲厚度比的a-σ_a曲线方法等，可查阅有关制品设计资料。