随机振动特性及其表示方法

随机振动是指未来任何时间内，振动因素的瞬时值不能精确预知的振动，如汽车行驶中任意颠簸、齿轮齿面上的疵点及间隙误差等都属于随机振动。随机振动的时间历程如图6-33所示。

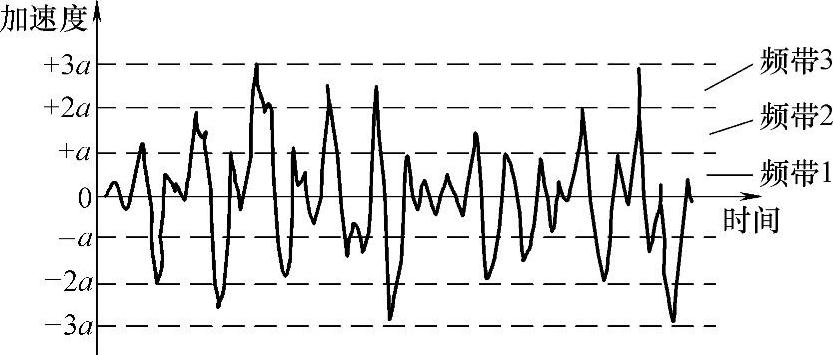
图6-33 随机振动的加速度变化曲线

从图6-33中可以看出其加速度的幅值，在时间历程中都按连续不规则的频率变化，且频率范围很广，可以分成若干个频带，而且有的频率与振体固有频率相同，还会发生共振。由于振动的随机性，所以只能用概率法来描述和计算振动规律。

1.随机振动特性参数

（1）功率密度D 它是表示在某频率范围内随机振动功率大小的概率值，故亦称为概率密度。其数学式为D=G²/（f₂-f₁），单位为g²/Hz。随机振动的输入、输出加速度因子a_i和a_o与D的关系式为

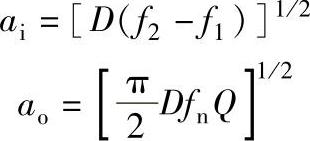
式中，f₂、f₁分别为随机振动范围内某频率（Hz）；f_n是固有频率（Hz）；Q是减振系数。

（2）概率密度曲线 由于随机振动中的位移、速度、加速度振动量的振幅随机而变，故只能用概率和统计方法中的正态分布规律来描述其变化规律，如图6-34所示。横坐标为某频率范围内出现的不同幅值，将相近的一组数据归为一类，分别用ΔX、ΔX₁……表示，以此大小排列组成横坐标。纵坐标表示各档ΔX值在时间历程中出现的次数相对于总次数的概率P。用两者组成的直方图，将顶线的中点连成曲线即为概率密度曲线。在曲线上的每一点，即表示该ΔX值出现的概率密度。所以表示概率密度的P值恒为正值，各档ΔX相应的概率之和等于1。曲线的最高点是指在随机振动中，某幅值出现次数最多的数值，在横坐标上的数值是正态分布的平均值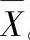。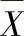与P及ΔX的关系式为

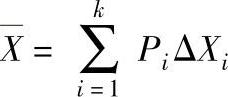
式中，ΔX_i是ΔX从第一档到i档的数据值；P_i是与ΔX_i相对应的概率值，计算举例见表6-11。

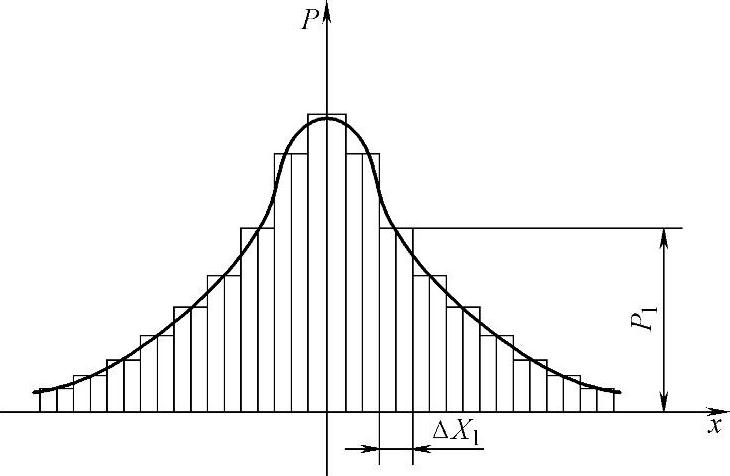
图6-34 幅值正态分布曲线

表6-11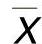的计算实例

（3）振动特性的标志值 由于随机振动的幅值大小的变化可用正态分布规律来表示。所以可用正态分布规律中的标志值来表示随机振动中振幅、速度、加速度的变化特性，主要标志值有如下一些：

1）平均值。平均值是指在随机振动中各种振动量的不同幅值中出现次数最多，最集中的数值，故可取平均值来表示全部幅值的大小。按计算方式不同可分为算术平均值、加权算术平均值等。算术平均值的计算式为

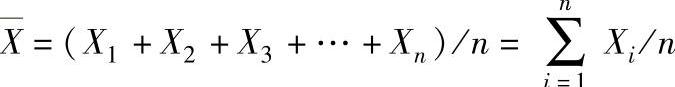
加权算术平均数计算公式为

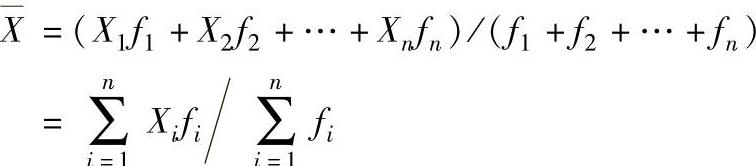
各式中X₁、X₂、…、X_n是不同幅值；i是测定次数，i=1、2、…、n；f是权数（频数）是指各幅值出现的次数或概率。但是在随机振动中，如此大的范围内所有幅值，仅用一个平均值来代表是不够确切的。(www.xing528.com)

2）均方值X_ms。由于简谐振动的功率或能量与振幅的平方成比例，因此用均方值也能显示幅值的特性。表示式为。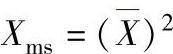

3）均方根值X_rms。均方根值能表示随机振动的能量，也能表示出现次数最多的振动峰值，所以它可作为位移、速度、加速度等振动量在随机振动的时间历程中所产生的不同振幅值的代表。也就是说，随机振动中不同大小的振幅值用它们的均方根值来表示较为确切，故称其为有效值，常用其表示各幅值，其表示式为

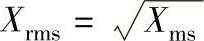
4）标准偏差σ。由正态分布曲线的特性可知，随机振动时所有不同的幅值是以最高概率值为中心向两侧分散分布的，称此为标准偏离（均方差），用σ表示，如图6-35所示，σ越大，则幅值越分散，在振动系统中大值、小值对平均值（最高概率值）偏离越大，振动特性越不稳定。偏离值的计算公式为

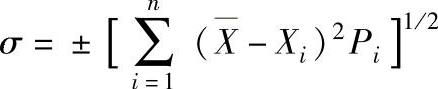
或

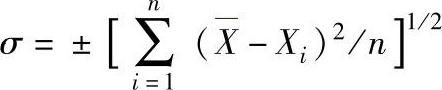
虽然均方根值能代表随机振动的幅值，但在-σ～+σ范围内的，仅占所有幅值的68.27%，如图6-36所示。在两侧-σ～-2σ及+σ～+2σ范围内的占27.13%，在-2σ～-3σ及+2σ～+3σ范围内的占4.33%，三者合计占总量的99.73%。虽然在随机振动的时间历程中从±2σ→±3σ所占的时间很短，但大多数情况都是在±3σ幅值时易发生振动破坏。

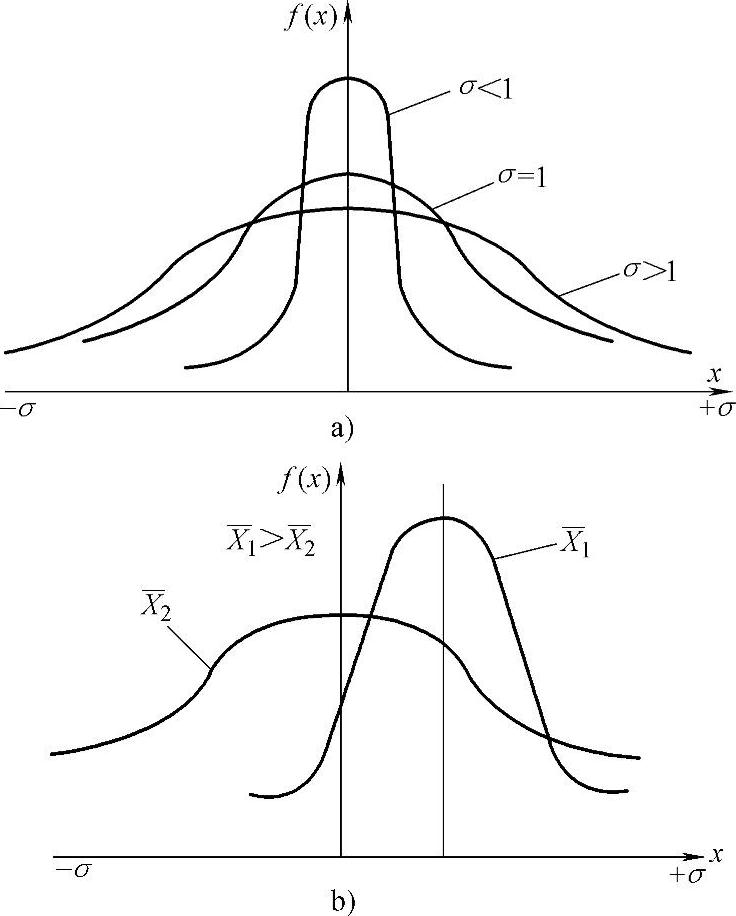
图6-3 5幅值分散性

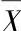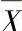a）相等 b）不等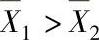

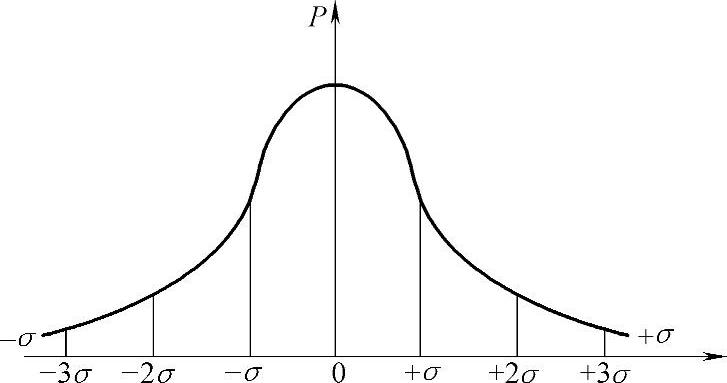
图6-36 -3σ～+3σ范围内概率分布比例

由于随机振动幅值的概率分布在-3σ～+3σ范围内的占有99.73%的幅值，因此在计算随机振动位移、速度、加速度的最大幅值时，应将其均方根值乘3倍，即最大幅值=3σ=3X_rms。如计算动态负载均方根，应按最大动态负载F_max=3Ga_rms来计算。例如静态负载G=8N，a_rms=15，则F_max=8×15×3N=360N。另外，在随机振动时，疲劳破坏多数由3倍动态负载引起的应力所致，其概率为0.0433，所以用F_max计算疲劳应力，按S-N曲线求得寿命次数N后计算寿命时间t时，应按t=N/0.0433f_n的公式计算失效时间t。

例：已知电路板固有频率f_n=95Hz，功率密度D=0.1g²/Hz，减振系数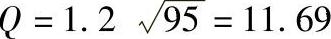，电路在随机振动条件下，中央变形量Y₀不得大于0.45mm，试校核电路板抗振性。

解：随机振动时电路板中央变形量Y₀′为

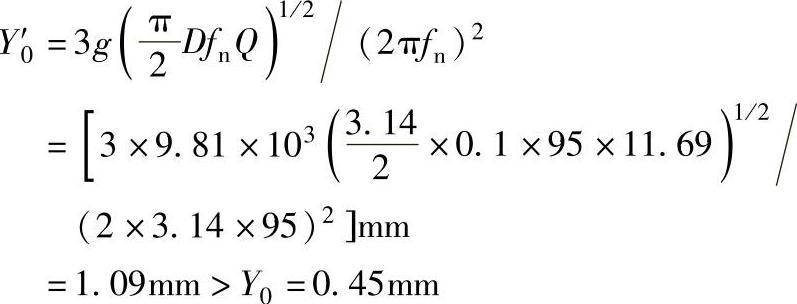
由此可知，在该振动环境下只有提高f_n值才可能降低变形量，以下式用Y₀=0.45mm时求f_n。

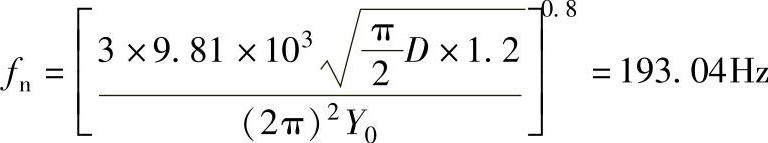
由此可见，只有提高f_n值，才可提高电路板的抗振性，为此可采取在电路板上增设加强筋或顶柱减振器等措施。