机械振动的形式很多,各有不同振动特性及计算方法。本节主要介绍几种常见的振动形式,如线性系统单自由度或多自由度振动、扭转振动及非线性系统随机振动等。
1.单自由度自由振动及受迫振动
单自由度振动是指在任意时刻,只用一个坐标就可完全确定各振动参数位置的振动系统,它属于线性振动,其中包括自由振动和受迫振动两种形式。自由振动系统是指振体被激振后立即撤去振源,让振体按其固有频率做自由振动,并在阻尼作用下逐渐衰减而静止。但在工程中经常遇到的是受迫振动形式,如图6-29所示。由外界不断地输入激振力,使系统发生振动。为此需要进行系统振动特性分析及抗振计算。
(1)单自由度受迫振动特性 以图6-29所示的系统为例,该系统的振动特性属于粘性阻尼。
激振力F=F0sin(ω·t)
运动方程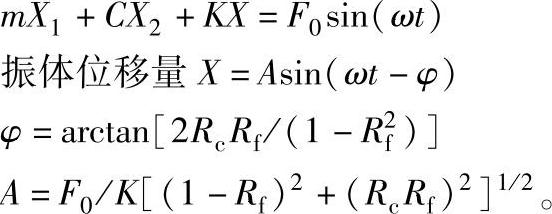
各式中,X1、X2、X分别表示振体在振动时间历程中随时间延伸而变的加速度,速度、位移等的各振动量;A是振幅(即振体最大位移);φ是激振力与振动位移之间的相位差;F是激振力;F0是外力;ω是角频率;t是时间历程中的某时间段;K是刚度;Rc、Rf分别是阻尼比及频率比。
(2)振动特性计算 激发振动的负载形式很多,如拉伸、弯曲、扭转等。任何形式的负载都需要先计算出激振力及动态应力,然后再利用不同模型相应的公式计算系统的振动特性。下面介绍几种常用的计算公式。
1)计算直线振动的激振力F。
F=F0sin(ωt)
F1=GaiQ=mgaiQ=mgao
式中,F是每一振动周期内,任何t时间段时的激振力;F0是外力(N);ω是角频率(rad/s);F1、G分别是动负载与重力(N);ai是输入加速度因子;m是静载质量(kg);g是重力加速度,g=9.8m/s2;ao是输出加速度因子;Q是减振系数;t是振动时间(s)。
2)计算动态应力。以激振力为作用力,代入不同受力形式的静态应力公式即可求得动态应力。
例如,已知矩形截面悬臂梁力臂为L,抗弯截面系数为E,动态激振力F,应力集中系数K,弯矩M=LF,则将动态激振力F代入静态抗弯应力公式,即可求得动态应力σ。
σ=KM/E=KLF/E
3)在单自由度激振力幅不变时,计算受迫振动的输入激振振幅Y0及输出最大振幅Ymax。
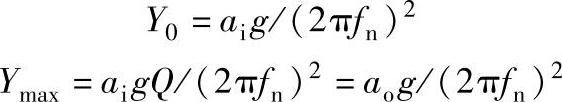
式中,Y0、Ymax分别是输入激振振幅和输出最大振幅(mm);g是重力加速度,g=9.8m/s2;Q是减振系数;fn是固有频率(Hz);ai、ao分别是输入及输出的加速度对g的因子,即重力加速度g的倍数,量纲为1,由工作环境条件测定。
Ymax值对悬挂的重物杆件可视为重物上下振幅值,对四周有约束的板件,则可视为中央的单向振幅。
4)计算Q值。Q值除了可用Rc、Rf计算外,它还可用Y0、Ymax及ai、ao来表示
Q=Ymax/Y0=ao/ai
同时,为了便于计算,在下列条件下可采用简化公式
①当低阻尼,即Rc<0.1、Rf=1、Q>10时,Q=1/2Rc。
②当单自由度振动系统Rf=1时,δ=[KG/g(Q2-1)]1/2。
③当单自由度振动系统Rf=1、Q>10时,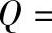
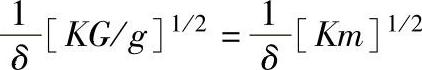 。
。
上面的Q值都是从系统中的Rc及Rf来计算的,但通过试验证明,Q值与fn成正比关系,fn大,则Q大,减振效率低。而且Q值还与塑件的结构与装配形式有关。通常,板件比杆(梁)制品减振效果好;盒、壳类制品比板件减振系数低。在系统中结构件之间接触或装配表面连接件多、振动件受约束、用料多,则阻尼大,因此通常按塑料件组合装配结构来计算Q的近似值。几种结构件Q值近似计算值见表6-10。
表6-10 几种结构件Q值近似计算值
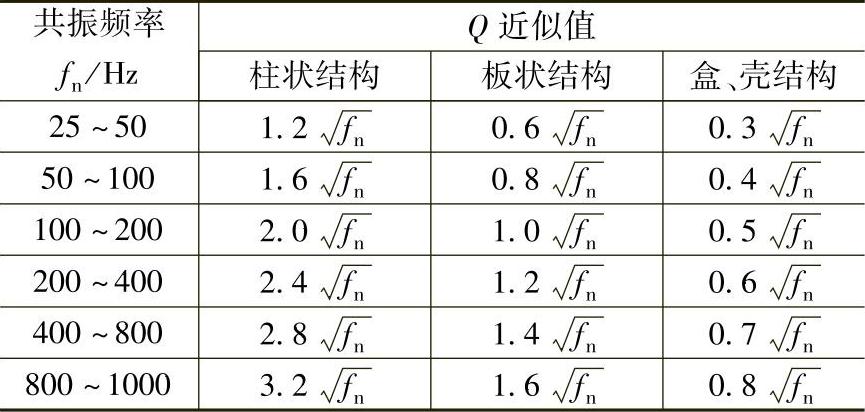
注:1.当制品的固有频率在本表中某档共振频率范围内时,就按本表中结构选用对应关系式计算Q值。
2.当激振加速度因子ai>2时,表内系数酌情提高,若ai>8,则应降低。
3.真空中的大面积板件若固有频率fn<50Hz,则将表内系数提高1.3~1.7倍。
4.扁平大面积板,若仅有自重,且四周固定fn<400Hz时,系数提高1.5倍。
5.多悬臂柱装配结构,表中系数提高2倍。
例:已知悬臂杆长L=0.3m,矩形截面宽b=0.015m,厚h=0.04m,材料密度为1060kg/m3,弹性模量E=1.4×104MPa,拉伸强度[σ]=50MPa,弯曲强度[σ0]=75MPa,杆端挂重物重力G=5N,悬臂杆重力G1=1.87N,激振频率f=40Hz,激振加速度因子ai=5,阻尼系数δ=300N·s/m,试求系统的工作安全性、寿命及振动特性。(https://www.xing528.com)
解:1)计算K及fn。从机械设计手册查得悬臂杆的K及fn公式为
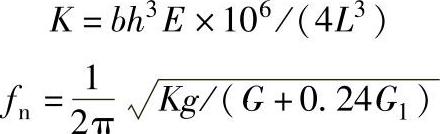
代入各已知数据,则可求得K=12.4×104N/m;fn=75Hz。
2)计算Rc、Rf、Q及Y0、Ymax。按前面介绍的公式可求得Rf=f/fn=0.53;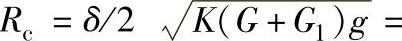
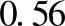 ;按表6-9求得
;按表6-9求得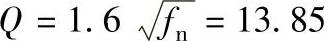 ,Y0=aig/(2πfn)2=2.2×10-4m,Ymax=Y0Q=3.04×10-3m。
,Y0=aig/(2πfn)2=2.2×10-4m,Ymax=Y0Q=3.04×10-3m。
该系统Q>10,Rf<1,Rc>0.50,所以不会发生共振。
3)计算激振力(动态负载)F。F=GaiQ=346.3N。
4)计算动态弯曲应力σ0(设应力集中系数K0=1)σ0=K0FL/w0,其中抗弯曲截面模量w0=bh2/6=4×10-6m3。
σ0=[1×346.3×0.3/(4×10-6)]MPa=25.9MPa<[σ0]=75MPa,故系统具有足够的动态弯曲强度
5)计算疲劳极限。该作用力属于对称循环应力,可利用S-N曲线求得工作寿命,也可用经验公式估算寿命。
[σ-1]=0.4[σ0]=30MPa,工作寿命N>107次,工作时间t=(107/75)s=1.3×105s≈37h。
2.多自由度受迫振动系统
在一个振动系统中由两个以上受迫振动体组成,且每一振动体都有各自的振动特性,则该系被称为多自由度受迫振动系统。例如,配电柜与电路板及电路板上的各种元件组成的系统即为多自由度系统,在振动时它们各自都有自己的振动特性,需用各个坐标来描述运动规律。图6-31所示为多自由度振动系统模型图。
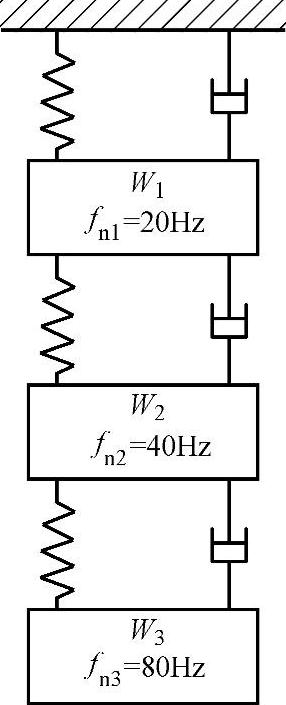
图6-31 多自由度振动系统模型图
图6-31所示为,由固定板W1、安装在固定板上的电动机W2及电动机上的减速器W3组成的多自由度系统。该系统的振动特性是由各单自由度振体的振动特性及各振体互相影响组合而成的,主要体现在下列几方面:
1)每一个单振体的输入激振力均来自于上一个单振体的输出激振力,以串联系统的顺序依次传递振动。
2)每一个单振体接受激振后按其自身特性发生振动,并向邻近单体发送输出振动。如果某单振体上有几个元件,则各元件都依同一输入振动为振源,各自按自己的特性进行振动运动。如在电路板上有许多元件,则电路板接受输入振动后产生的输出振动,即为各元件的输入振动。同时,为防止发生共振,在串联系统中各单振体的固有频率应为激振频率的两倍以上,该规则称为倍频规则。如图6-31所示,fn1=20Hz、fn2=40Hz、fn3=80Hz。
3)串联系统的整体减振性能可用两者合一的组装件的减振系数来表示。
Q=Rq1
ao=Raiq21
式中,q1是单振体减振系数;Q是由q1组件组装后,两者合一的组装件的减振系数;ao是组装件的输出振动加速度因子,为重力加速度的倍数;R是组装件减振系数占单件减振系数之比值,可用曲线来表示如图6-32所示。
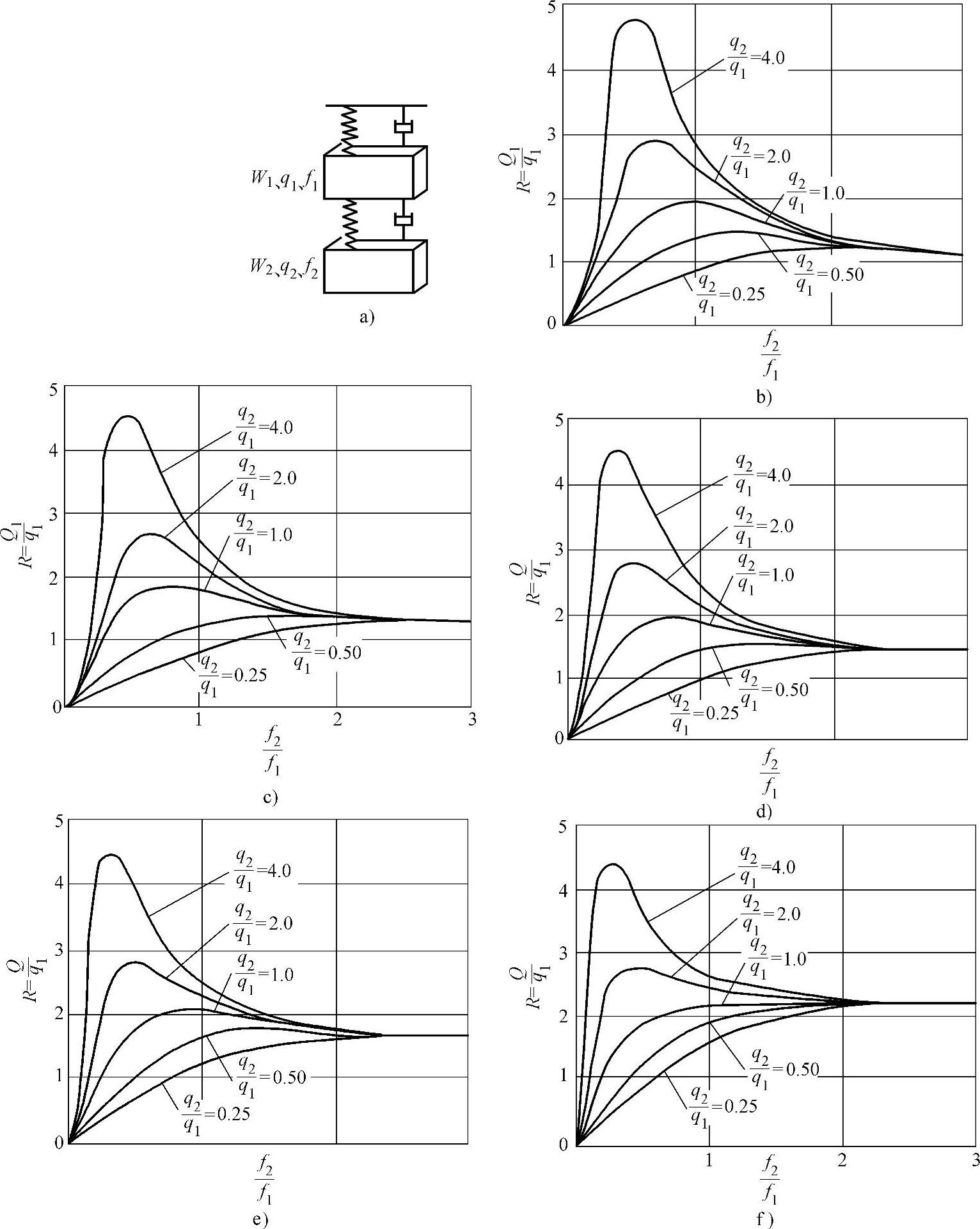
图6-32 组件减振系数Q与单件减振系数q1之比值R
a)系统模型 b) c)
c)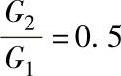 d)
d)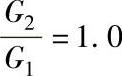 e)
e)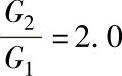 f)
f)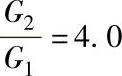
图6-32所示的是由两个单振体串联组成振动系统的结构及其特性曲线,计算时首先用表6-9,求出q1、q2,然后用G2/G1、f2/f1、q2/q1,查图6-32的曲线求出R,从而求出W2输出的ao、Ymax等参数。
例:现有电器箱、电路板导轨、电路板(四周约束),电路板上元器件组成的串联多自由度受迫振动系统,试分析电路板振动特性。
已知导轨的固有频率fn1=40Hz,加速度因子ai=5,重力G1=8N;电路板尺寸h(厚)×b(宽)×L(长)=0.0015m×0.15m×0.22m,重力G2=2N,弹性模量E=2×104MPa=2×106Pa,泊松比ν=0.12。
解:由于电路板上的元件质量很小,故视同与电路板为一体,则该系统变成由导轨及电路板组成的两单自由度系统,但电路板的输出加速度必须小于各元件能承受的最大加速度75g。
1)计算导轨、电路板减振系数q1及q2。按表6-9可求得导轨减振系数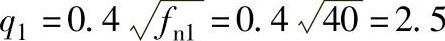 。电路板减振系数
。电路板减振系数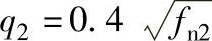 ,而
,而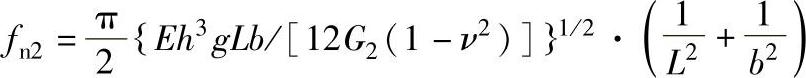
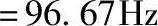 ,则
,则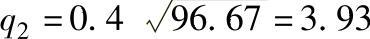 。
。
2)计算R值。G2/G1=0.25;fn2/fn1=2.4;q2/q1=1.57按图6-32b可求得R=1.2。
3)计算电路板ao及Ymax。ao=Raiq21=37.5,Ymax=ao·g/(2πfn2)2=1.005mm。因为aog=37.5g<75g,所以该结构可通过振动试验。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




