机械振动的类型很多,但基本特征和组成要素是相似的。当某物体发生振动时,必然会有位置往复移动,其中包括位移量大小、往返速度及随时间延长中的运动规律(又称振动的时间历程)。如果运动规律呈正弦或余弦曲线演变,则称为简谐振动,这是一种常见的振动现象,是一种振动量值每径相同的时间间隔,其振动量值会重复出现一次的振动,称其为周期振动。下面按简谐振动形式来介绍振动的特征及参数。
1.简谐振动的时间历程
图6-26所示为简谐振动的振动量值(包括位移值、速度值及加速度值)在时间历程中沿正弦曲线的运动规律。

图6-26 简谐振动运动规律
图6-26中横坐标为时间历程t,纵坐标为振动体各振动量值,包括位移量、速度、加速度。图6-26中表示了三项振动量随时间历程的振动运动规律,各曲线的最大值(峰值)即为该振动量的幅值。振动每循环一次的时间间隔称为振动周期T。周期的倒数,即为每秒振动次数,称为振动频率f,单位为Hz,当频率以每秒弧度(rad/s)表示时称为角频率ω,即每2π秒振动的次数,也称为圆频率。T、f、ω与振动次数n之间的关系为
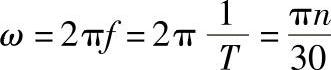
图6-26a为各振动量值在x-y坐标轴上的投影,用矢量方式来表示各量值在时间历程中的变化规律,其含义为当矢量A以等角速度ω做逆时针方向旋转时,用它在纵轴(或横轴)上的投影表示振动-时间的关系。
2.振动量要素
振动体的简谐振动由振动体位移、振动速度、加速度三个要素组成。下面介绍各要素的定义及在时间历程中某时段的量值计算公式。
(1)幅值 它是指各振动要素在正弦曲线上的最大值,亦称峰值。
振动幅值的表示形式如图6-27所示。

图6-27 幅值表示形式(https://www.xing528.com)
图6-27中的曲线为周期振动图形,简谐振动运动方程为

幅值可用五种形式来表示。
1)峰值A。它是在给定时间段xt的最大值,即图6-27中的A值。
2)峰-峰值AFF。它是在给定时间段xt的最大值和最小值之差,幅值为2A。
3)平均绝对值 。它是周期T内平均绝对值,
。它是周期T内平均绝对值,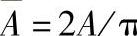 。
。
4)均方值Ams,Ams=A2/2。
5)均方根值Ar·m·s(有效值),
 。
。
各种形式的幅值可用于不同的表示方法。
(2)振幅 它是指位移的幅值,即振动体离开其平衡位置的最大位移值,即图6-27中的A值,任意时间的位移量x=Asinωt。
(3)振动速度 从矢量图上可以看出,振动体的振动速度比位移矢量超前90°,即振动速度与位移有相位差。最大速度为vmax=ωA,任意时段的速度
(4)加速度 加速度矢量比位移矢量超前180℃,它与振动速度,位移都有相位差。最大加速度amax=ω2A,任意时段加速度值
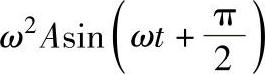 。
。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




