疲劳强度计算与设计要求

由于疲劳形式很多，各种形式有不同的计算方法，本书仅介绍几种常见的计算方法。

1.常规疲劳计算

所谓常规疲劳是指制品在低负载交变应力作用下，疲劳寿命>10⁵次的疲劳形式。按制品使用要求可分为两种形式：一种是要求使用寿命大于10⁷次，长期使用不发生疲劳破坏的，称为无限寿命设计；另一种是只要制品达到一定使用寿命即更换，但要求减轻制品的质量，提高性能，称为有限寿命设计。两种方案各有不同设计方法，但有一点是相同的，即制品在工作中承受的不同形式应力都作为发生疲劳的循环应力，然后乘安全系数或修正系数后作为实际循环应力，该应力要小于材料允许应力，依此为基础进行疲劳计算，设计制品。

（1）无限寿命计算计算方法举例如下：

1）单向应力常规疲劳计算。

例：用ABS塑料制造的简支梁塑料轴，危险截面在支点内侧l=10mm处，直径d=10mm，简支梁支点间距中心位置受F100N的对称循环载荷作用，现校核危险断面的疲劳强度及预测寿命。

解：危险断面弯曲应力σ=16Fl/（πd³）=5.09MPa。

疲劳极限σ_-1=σ×k（安全系数）=5.09×2=10.18MPa。

查图6-4可知，ABS的σ_-1≈18MPa。

因此，该制品符合无限寿命要求，N>10⁷次。

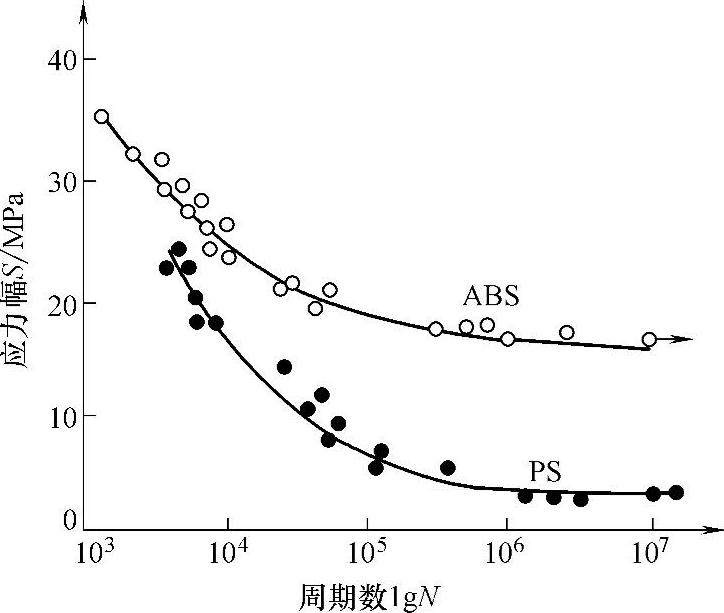
图6-4 PS（19个试样）ABS（21个试样）单点法测定的S-N曲线

2）多向应力常规疲劳计算。当制品受到多方向应力时，可用各向的主应力幅值及平均应力值计算出多向当量应力幅值及平均应力值，然后将当量值按单向应力常规疲劳计算方法进行疲劳计算。多向当量应力幅值及平均应力计算公式如下：

①多向当量应力幅值计算公式

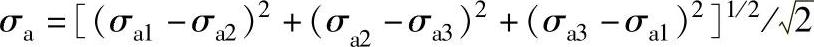
②多向当量平均应力计算公式

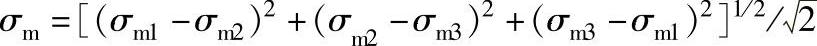
③双向当量应力幅值及平均应力计算公式

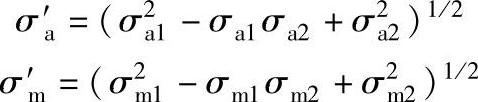
式中，σ_a1、σ_a2、σ_a3及σ_m1、σ_m2、σ_m3分别是多向应力时各单向的主应力幅值及平均应力；σ′_a、σ′_m分别是双向应力时各单向主应力幅值及平均应力。

（2）有限寿命疲劳计算 制品的使用期限规定在10³～10⁶次循环次数范围内的寿命称为有限寿命，这种制品使用时间达到规定寿命后，即使零件完整无损也必须更新，对零件要保证强度，结构轻巧，如航空零件等。其计算方法与常规计算相似。其计算原则如下：

1）强度条件是循环应力（工作应力）小于强度允许应力。

2）在满足规定使用寿命条件下，循环应力小于疲劳强度。

例：用POM制作的齿轮，齿数Z=48；压力角为20°；齿宽b=34mm；转速n=100r/min，工作环境温度为23℃，传递功率P=0.1kW，综合修正系数k=4.11，使用寿命5×10⁵s，求该齿轮模数。

解：从图6-5所示的S-N曲线查得5×10⁵s时弯曲应力幅值σ_-1=30.8MPa≤[σ]=100MPa。

从齿轮弯曲疲劳应力公式推导出模数计算公式为

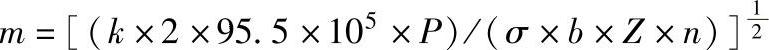
代入各数可求得m=1.25mm。该齿轮符合有限寿命疲劳设计的要求。

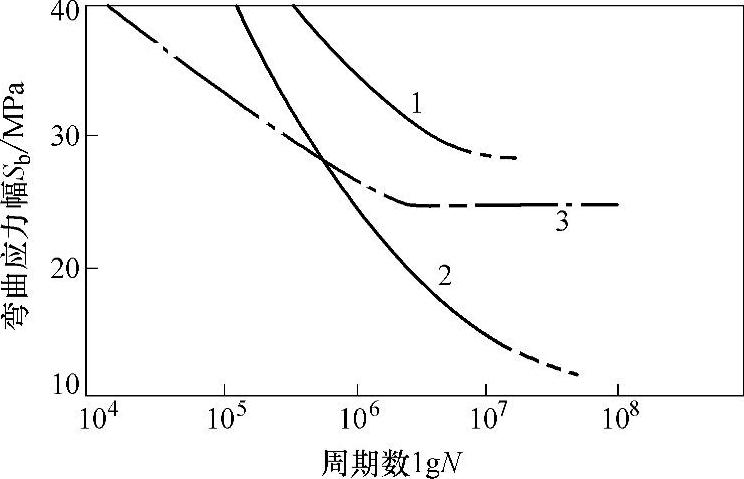
图6-5 几种材料的弯曲疲劳曲线

1—23℃时PC+10%玻璃纤维 2—23℃未充填PC 3—23℃POM/[美]塞兰尼斯M90

（3）应力集中系数及安全系数

1）应力集中系数。在计算塑料制品疲劳性能时，应力集中系数是必须要考虑的问题。需按塑料制品的尺寸形状、表面状态等方面来分析应力集中的可能性，并用修正系数补偿。

塑件的缺陷包括表面凹凸、尖角、缺口、沟槽、圆孔、壁厚不均匀、表面加工痕迹、凹坑银丝、流痕、擦伤、划痕、熔接缝、表面粗糙、细小裂纹、合模线及接合强度、内应力、气泡等缺陷都会引发应力集中，因此需按不同情况选用应力集中系数来计算设定的最大应力。应力集中系数可分为理论应力集中系数和有效应力集中系数两种。

理论应力集中系数是指按弹性理论计算出的缺口或其他应力集中源的最大应力与相应标称应力之比值，也就是假设材料是均匀、各向同性的，在弹性极限范围内时只考虑零件几何形状来决定的系数。

有效应力集中系数是指对应于同一寿命的无应力集中试样的疲劳强度与有应力集中试样的疲劳强度之比（又称为疲劳缺口系数）。它是按材料局部区域发疲劳时，材料的应力已超过屈服强度，部分材料产生塑性变形进入弹塑性状态的情况来计算应力集中系数的。本书仅介绍理论应力集中系数K。

K=σ_max/σ

式中，σ_max是发生应力集中时产生的最大应力；σ是理想材料不计应力集中时材料允许应力或制品承受的循环交变应力。

几种情况的应力集中系数如图6-6～图6-10所示。

例：已知某制品承受的弯曲应力为11.25MPa，弯曲疲劳强度S_-1=28MPa，查得应力集中系数K=1.62。

解：σ_max=11.25×1.62MPa=18.2MPa<S_-1，故该制品符合疲劳强度要求。

2）安全系数。在计算塑料制品疲劳强度时，除了考虑应力集中系数外，还需单独考虑安全系数。根据不同情况选用安全系数，参见表6-4。

表6-4 许用安全系数[n]_-1（参考值）

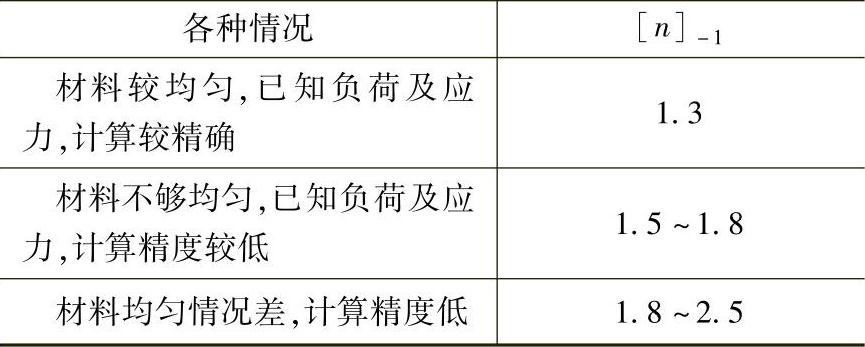
此外，安全系数与受载情况有关，对称循环的[n]_-1比不对称循环的[n]_-1大；恒幅循环的[n]_-1比变幅的[n]_-1大。N≤10³时的[n]_-1比N≥10⁷时的[n]_-1大。

例：已计算出弯曲应力σ=11.25MPa，弯曲疲劳极限S_-1=28MPa，应力集中系数K=1.62，材料质匀，应力计算精确，允许[n]_-1=1.3，求实际安全系数。

解：计入应力集中系数的最大应力为

σ_max=σ^K=18.2MPa

安全系数[n]=S_-1/σ_max=1.54>[n]_-1=1.3，故制品设计符合安全系数要求。

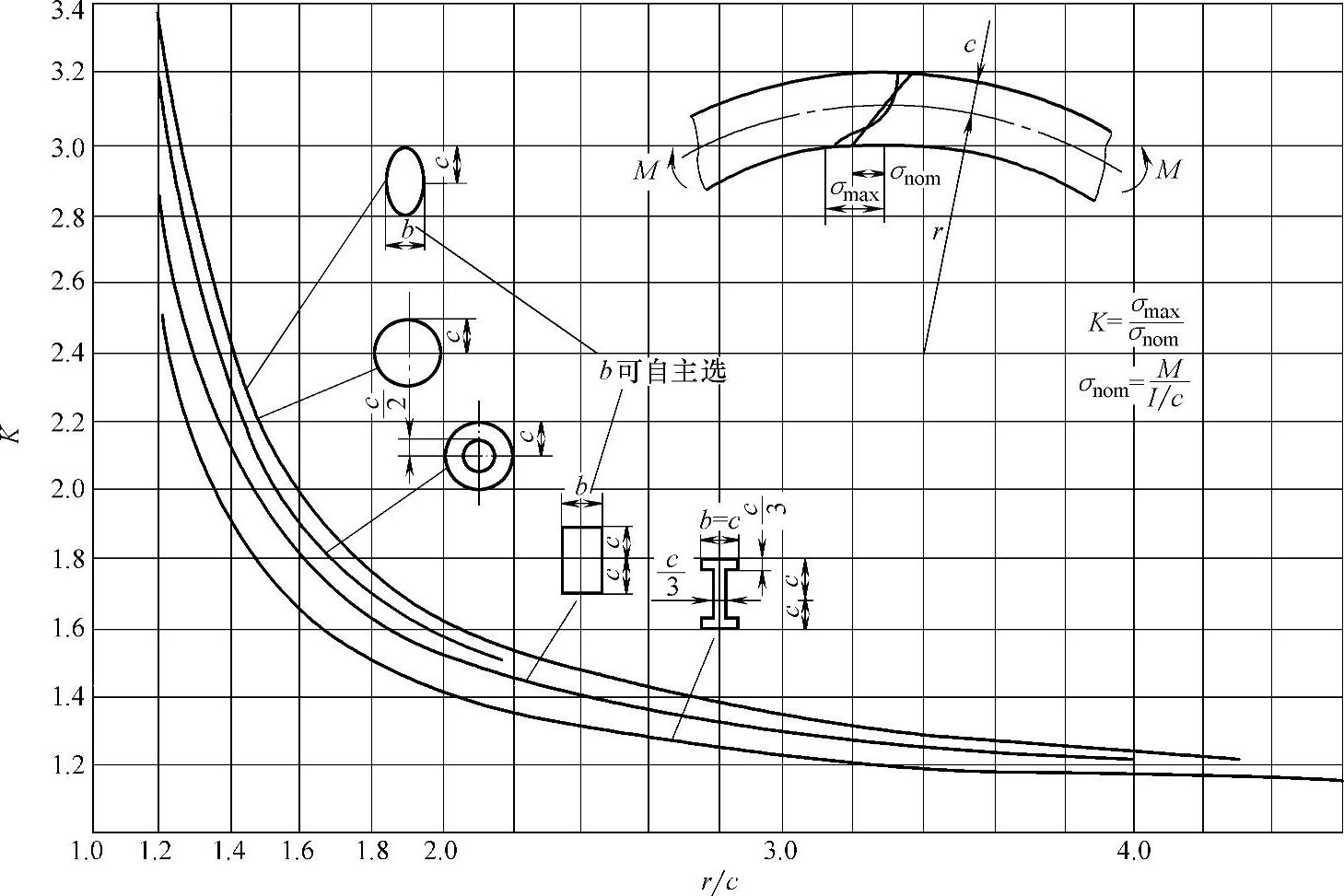
图6-6 不同截面弧形柱体受弯曲作用时应力集中系数K

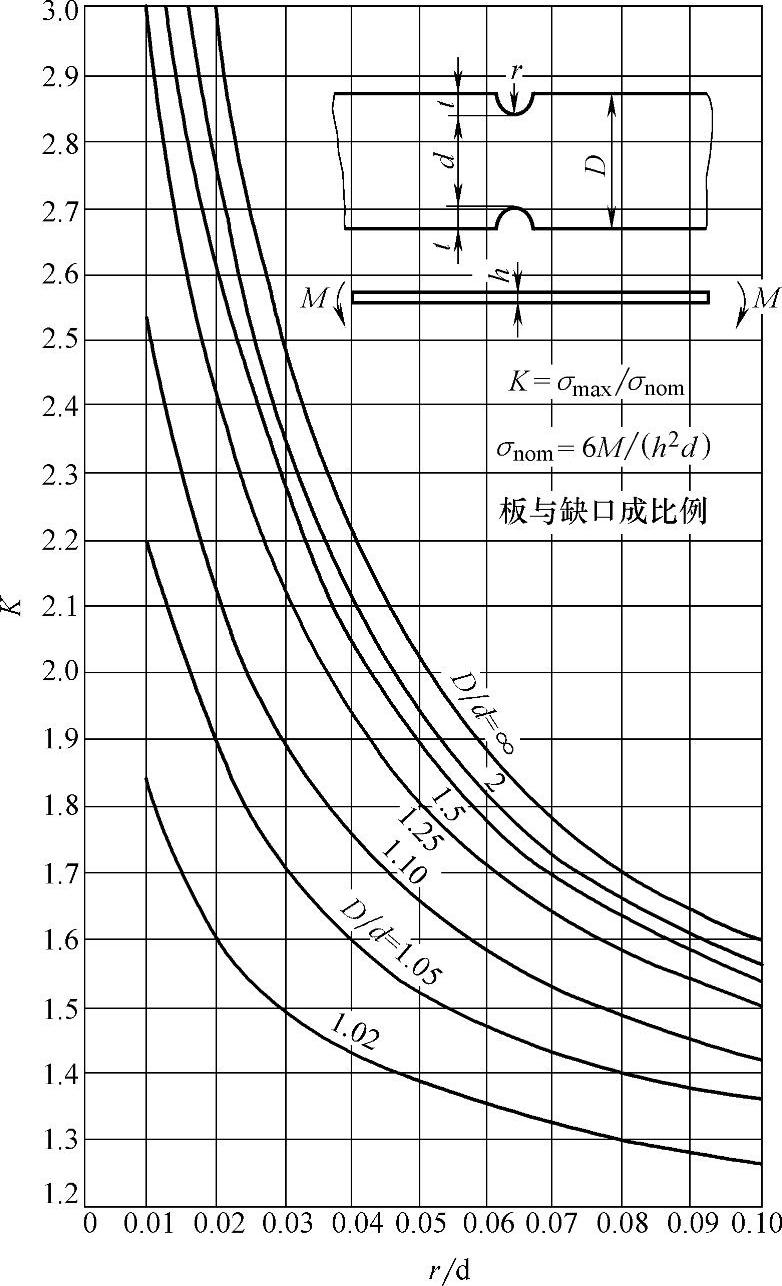
图6-7 带缺口板件受弯曲作用时应力集中系数K

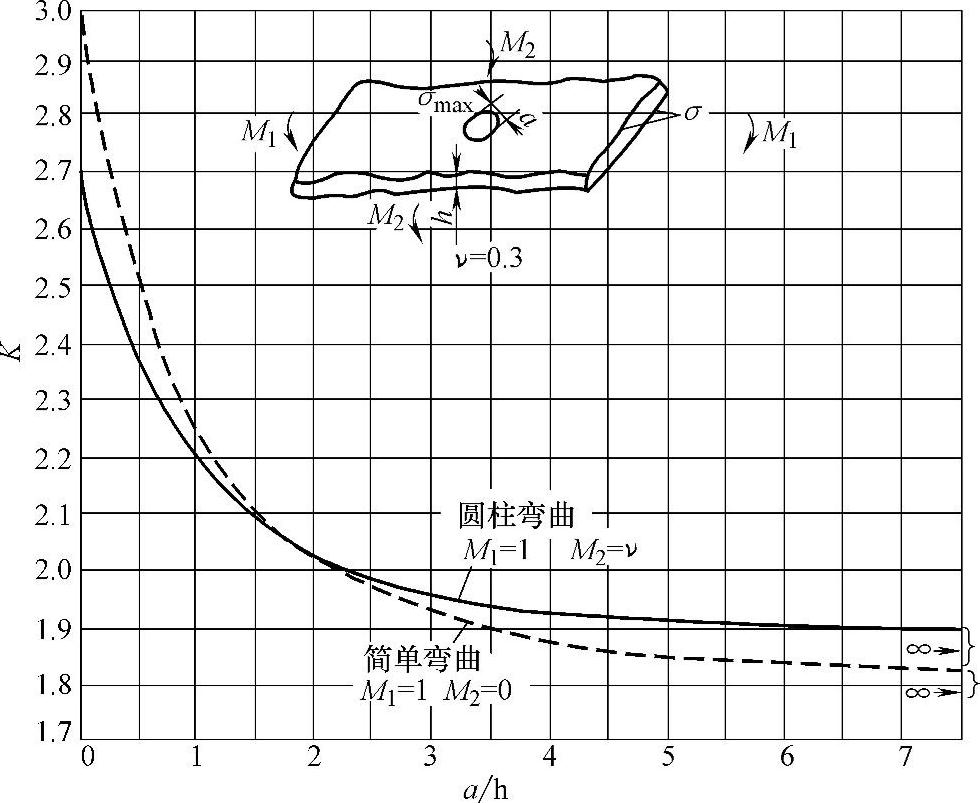
图6-8 有一孔无限宽度板件的应力集中系数K

简单弯曲：不计泊松比影响

圆柱弯曲：要考虑泊松比ν

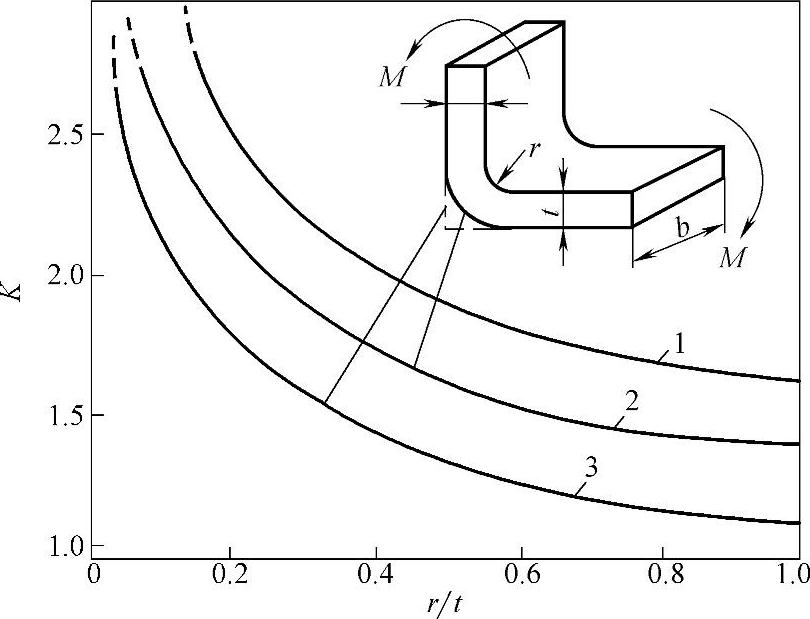
图6-9 弯折件里外圆角应力集中系数K

1—里外都是锐角 2—壁厚均匀 3—外侧锐角

2.寿命的估算

在有限寿命计算中，经常会遇到估算制品使用寿命的课题，以便控制使用期限，及时更换新制品，寿命估算有以下两种方法：

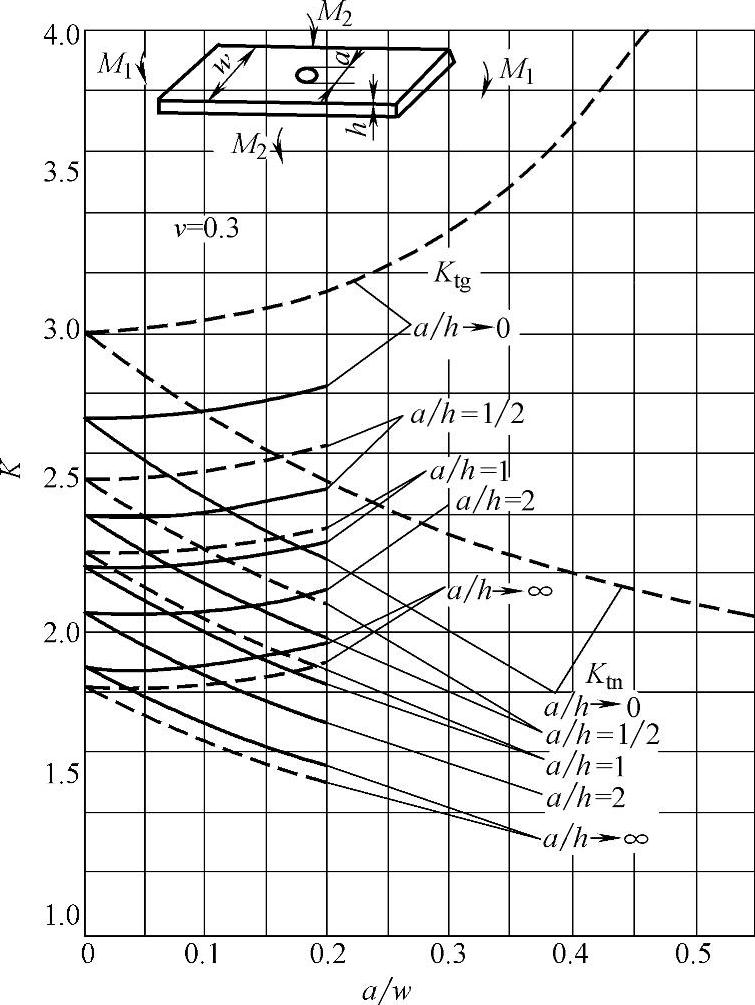
图6-10 有一孔有限宽度板件的应力集中系数K

实线—圆柱弯曲虚线—简单弯曲K_tg—宽度方向弯曲K_tn—长度方向弯曲

1）当应力幅度恒定不变时，可根据确定的制品上危险点的应力幅度查S-N曲线，借此可求得循环次数。

2）当应力幅度为变值时，则可用下列公式计算N值。

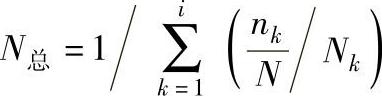
式中，N是制品在各种应力幅度下工作循环次数之和；n₁是制品在某一应力幅度之下工作循环次数；如制品在σ_a1、σ_a2、…、σ_ai共计工作循环次数为100次，而在σ_a1时只工作10次，则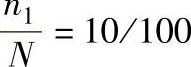；N_k是当σ_a=σ_ak时，从S-N曲线中查找的对应循环次数。

例：用GFPA（33%）材料作挂杆，工作环境温度为23℃，相对湿度为50%，每天要挂卸不同的重物100次，具体情况见表6-5。试估算挂杆的使用寿命。

表6-5 挂杆每天工作情况汇总(www.xing528.com)

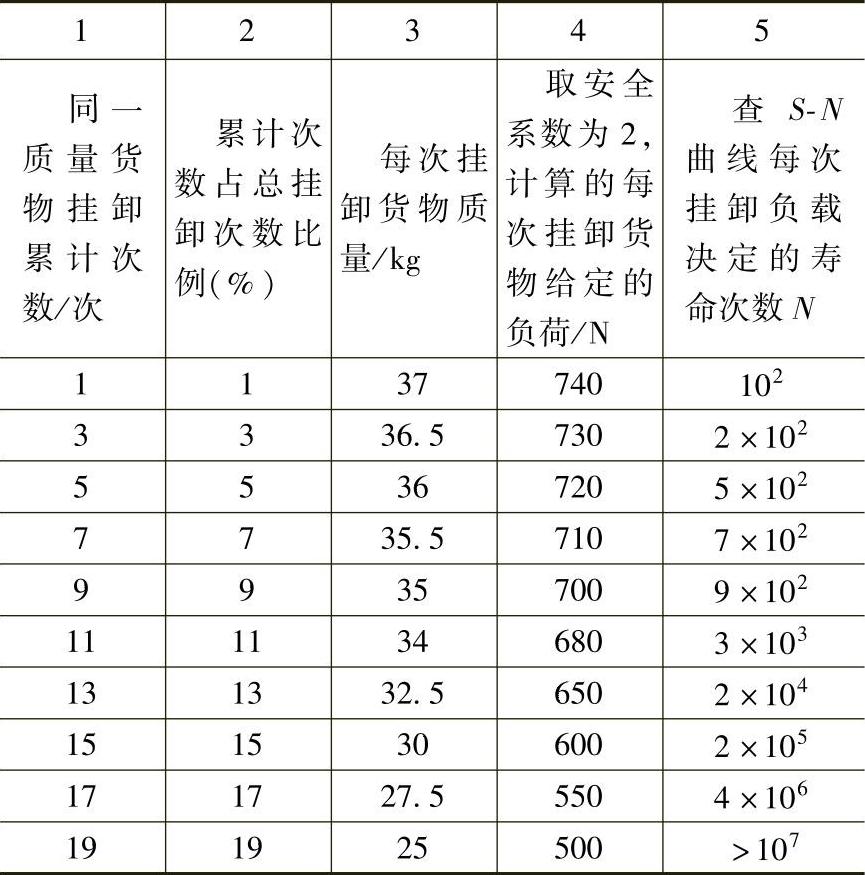
解：首先可确定挂杆是承受脉冲循环变幅应力的，则将同一质量货物挂卸累计数填入表6-4的第一列。

计算每一档累计次数占总挂卸次数的比例填入表第二列。

将每种货物的质量及乘安全系数后的挂杆负载分别填入表6-4的第三列，第四列即作为挂杆每次受到的可变负载。

用经验数据计算循环应力幅值。

1）从资料查得GFPA66（33%）的拉伸强度σ_b=160MPa。

2）先求出σ_-1，再换算求出σ₀。

对称循环拉压应力的疲劳极限σ_-1=0.3×160MPa=48MPa。

对称脉冲循环应力的疲劳极限σ₀=1.4×σ_-1=67.5MPa。

由于σ₀大于多数挂杆承受的负载，所以制品应按有限寿命进行疲劳计算。

按GFPA66拉压S-N曲线，绘制图6-11所示S-N曲线，按第四列中的负载求出相应的寿命次数N，将其填入表6-4中第五列，则N_总为

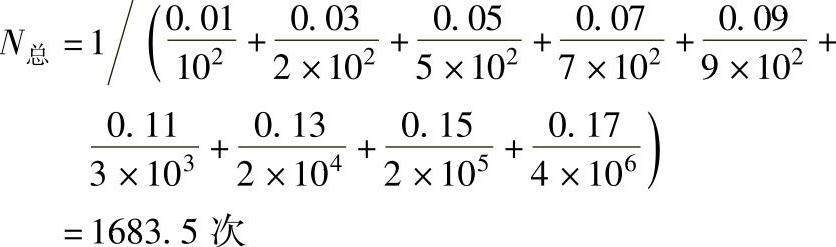
按每天100次计，有限寿命为16.8d。

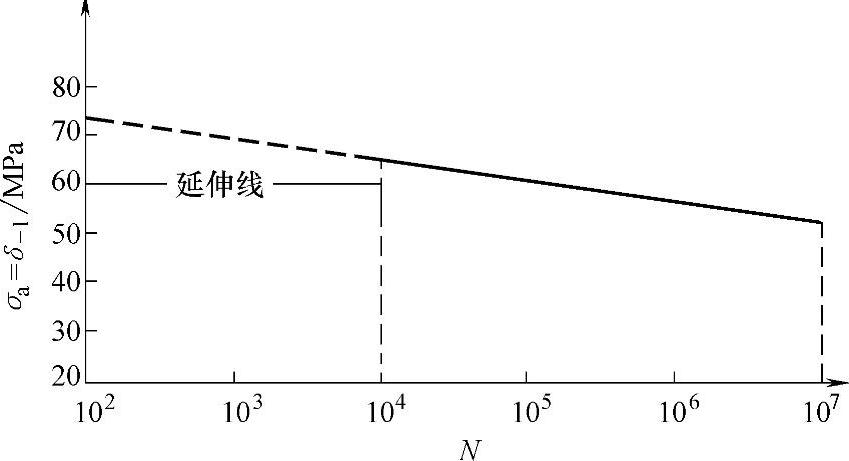
图6-11 挂杆拉压S-N曲线

3.裂纹扩展寿命计算

裂纹扩展寿命计算又称为损伤容限设计方法，它是根据零件上有裂纹存在时在受拉伸力情况下裂纹扩展的规律来计算制品寿命的。

（1）参数计算法裂纹扩展寿命计算参数如下：

1）裂纹尖端应力强度因子K。它是指制品上有长度为a₀的裂纹时，在静态拉伸应力σ的作用下裂纹尖端产生的应力。

2）临界裂纹尺寸a_c当拉应力σ增大时K也增大，裂纹a₀随之扩展，当制品断裂时的裂纹长度，即为临界裂纹尺寸a_c。

3）临界应力强度因子K_c它是指制品断裂时应力强度因子，又称断裂韧度，表征材料抗裂纹开裂的能力。K_c值越大，材料抗裂性越好。K_c随材料厚度增大而下降。

4）裂纹扩展速度da/dN。它表示单位循环次数裂纹扩展的长度，单位为mm/次。

5）应力强度因子幅度ΔK。它是指裂纹按da/dN速度扩展时，起始K和后续增大K值之差，即ΔK=K_max-K_min，对应作用于裂纹上的应力Δσ=σ_max-σ_min。如果σ_min=0，则ΔK=K；当制品断裂时，ΔK=K_c，其单位为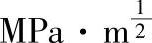。如果不考虑试样应力系统的边界条件，则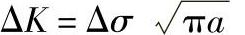

6）da/dN-ΔK曲线该曲线又称为疲劳裂纹扩展（FCP）特性曲线，如图6-12所示。da/dN与ΔK呈指数函数关系。在应力作用下随着ΔK的增大，da/dN以不等速率增大，在Ⅰ区为初始稳定区，da/dN→0时的ΔK值称为疲劳裂纹扩展应力强度因子门槛值ΔK_th。随着ΔK的增大，在Ⅱ区时da/dN与ΔK成正比关系增大；当ΔK继续增大，在Ⅲ区时da/dN急速增大，导致裂纹断裂，此K值即为临界应力强度因子K_c。da/dN与ΔK也可用下列方程表示

da/dN=A（ΔK）^m

式中A、m———材料常数，可用FCP曲线求解。

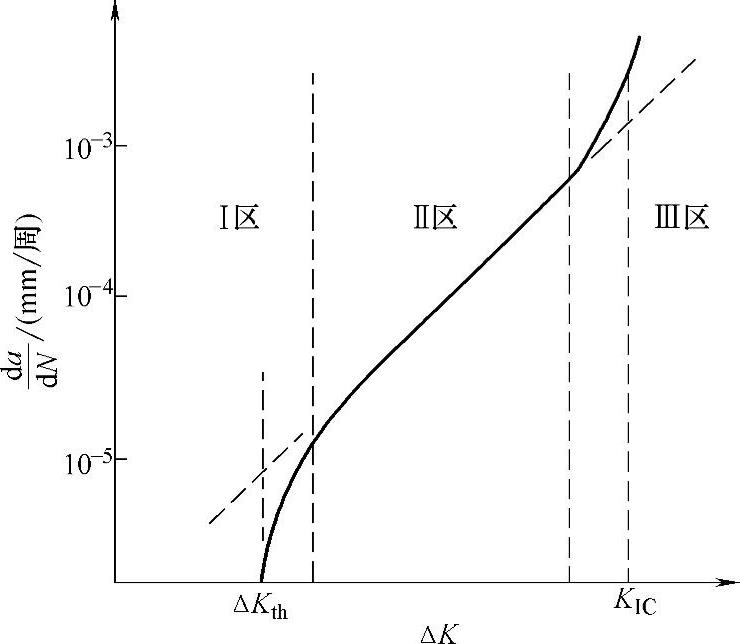
图6-12 da/dN-ΔK曲线

图6-13所示为PMMA的FCP曲线，从中任意取两个ΔK值，1.6及0.5即可求得相对的da/dN值7.9×10^-6及1.7×10^-7，分别代入则可得联立方程：

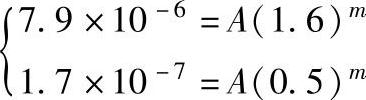
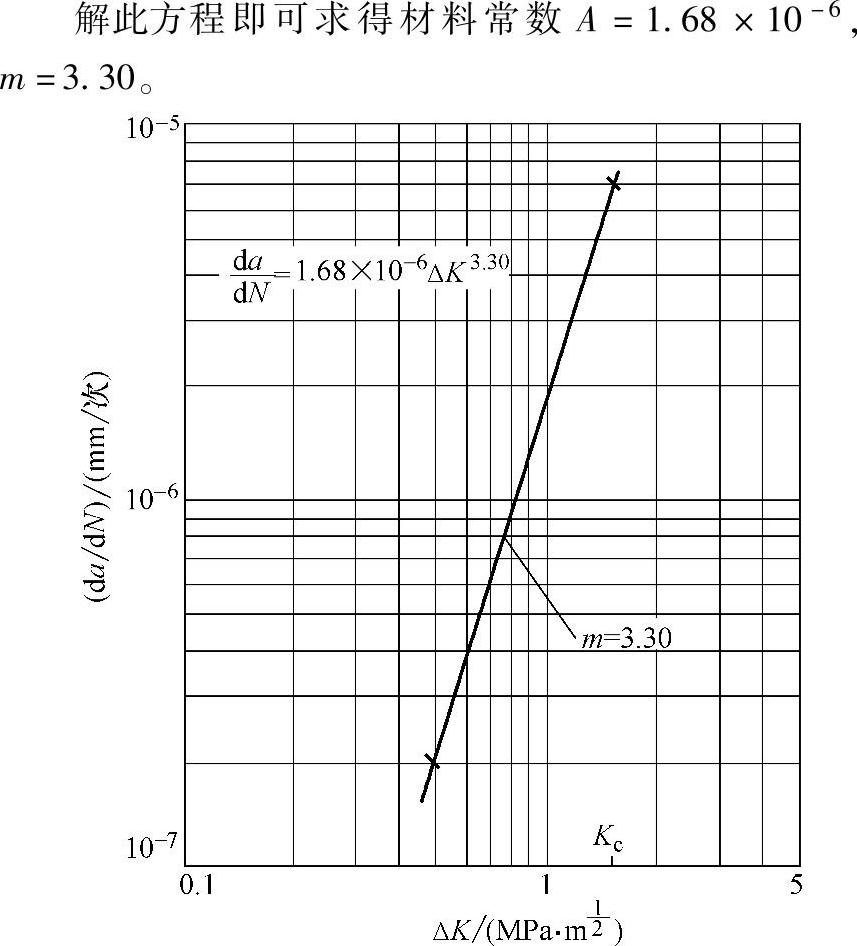
图6-13 PMMA的FCP曲线

不同材料及不同应力比的FCP曲线也不同，如图6-14所示。

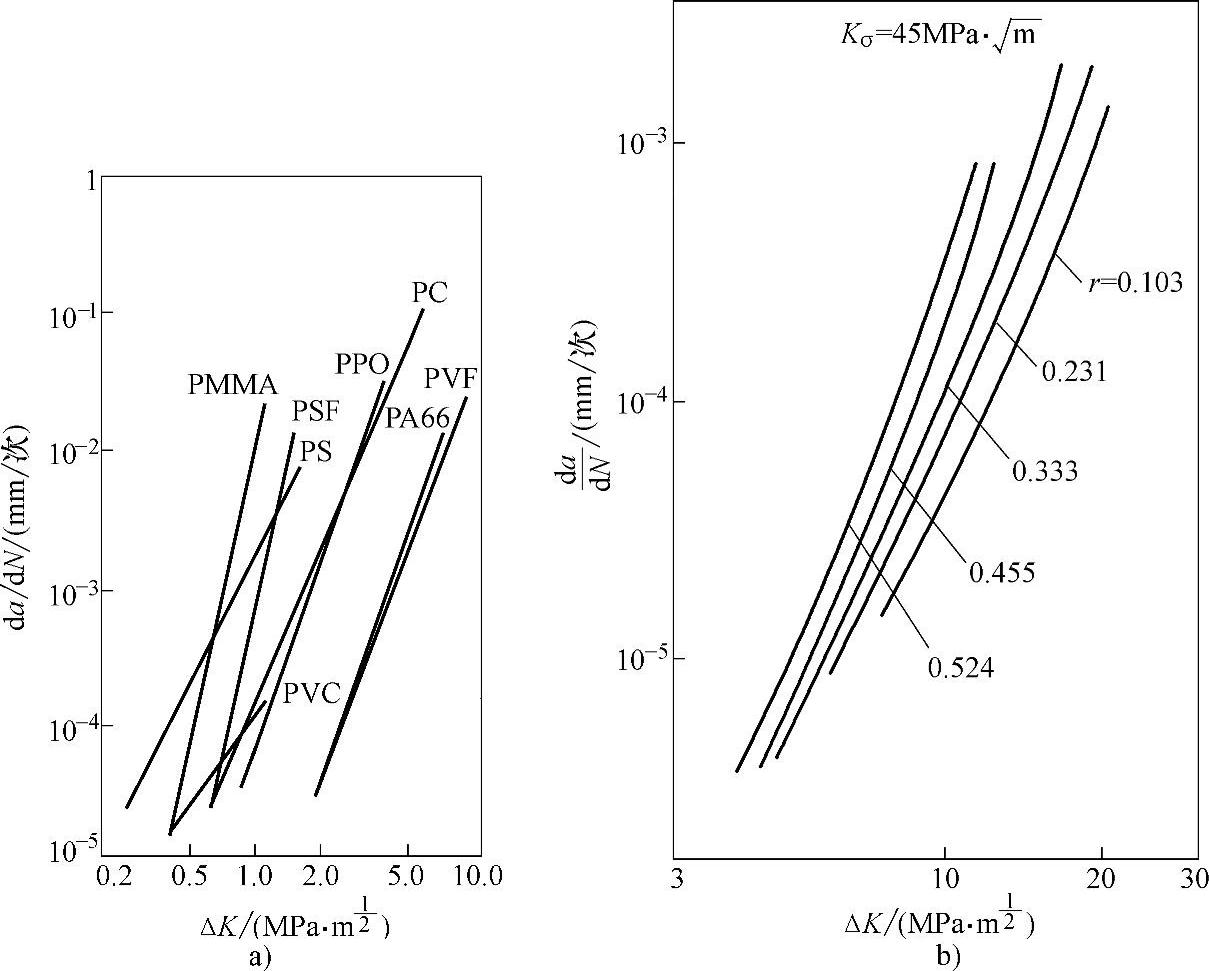
图6-14 不同材料及应力比的FCP曲线

a）8种高聚物的疲劳裂纹扩展的特性曲线 b）应力比对（da/dN）-ΔK的影响 PSF—聚砜 PVF—聚氟乙烯

（2）用FCP曲线计算疲劳寿命根据上述关系可列出下列方程式

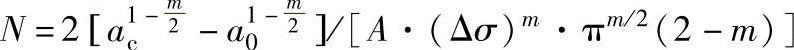
式中N———断裂循环次数；

Δσ———作用裂纹上最大应力与最小应力之差，当最小应力为零时，ΔK=K_c（即为裂纹扩展终止点应力强度因子）；

A、m———材料常数；

a₀、a_c———初始裂纹长度及裂纹扩展终止临界裂纹长度（mm）。

在选择a₀及a_c时要注意以下两点。

1）a_c的计算式与制品受力形式有关。如板状制品上的裂纹在拉伸时呈平面应变状态，则a_c=K²_c/（σ²·π）。如果在圆周表面沿轴向有裂纹，在高速旋转时周向循环应力导致裂纹扩展，则应按圆片形应变状态计算，a_c=（K_c/2σ）²-π。其他应变形式的a_c计算公式需从断裂力学资料中查找。

各式中的σ为循环应力幅，单位为MPa，K_c为裂缝应力强度因子，单位为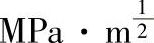，为FCP曲线上裂纹扩展终止时横坐标上的ΔK值。

2）a₀值与裂纹形状有关，通常可分为三种类型，如图6-15所示。

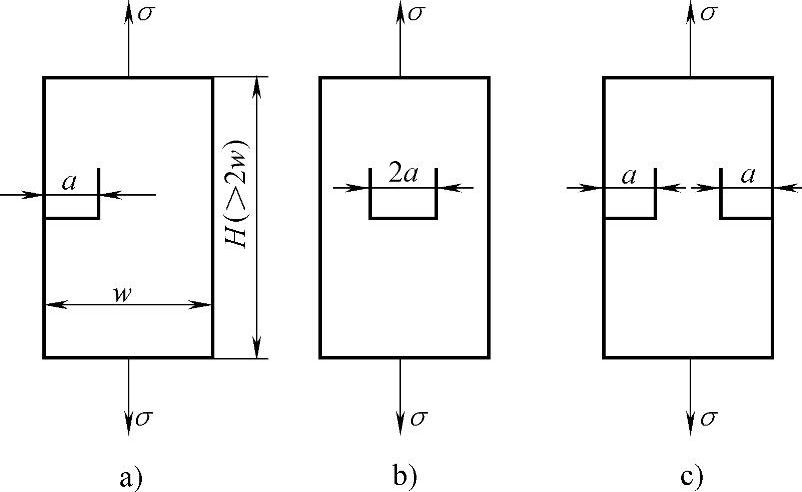
图6-15 拉伸张开型三种裂纹形式

a）单边裂纹拉伸 b）中心裂纹拉伸 c）双边裂纹拉伸

如果计算图6-15b所示的类型裂纹寿命，寿命公式中的a₀值应减半代入。

例：已知PC塑料制作的回转轴，发现表面上沿轴向有长0.5mm的裂纹，周向循环应力幅值σ为20MPa，求a_c及N。

解：1）计算K_c值。根据PC的FCP曲线的裂纹终止点，在ΔK横坐标查得相应的K_c为。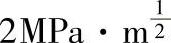

2）计算a_c值。将已知数代入圆片形裂纹应力强度因子计算式得

a_c=（K_c·π/2σ）2/π=7.85mm

3）计算常数A及m。从PC的FCP曲线取ΔK=0.5、ΔK=1.0两点代入da/dN=A·（ΔK）m，得两个方程式

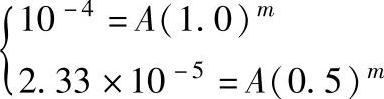
解联立方程式求得A=10^-4，m=2.1

4）计算N值。将已知数代入N公式，此时a₀取半值，即a₀=0.25mm，则

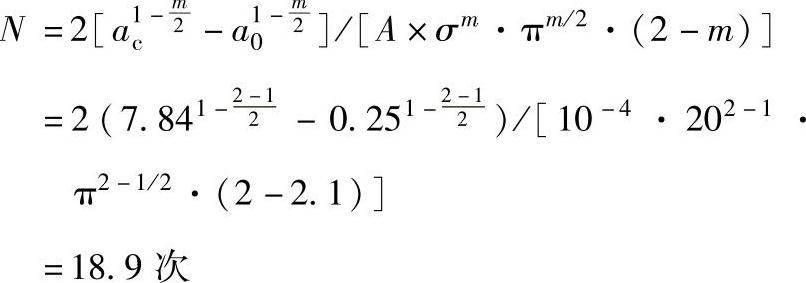
计算结果显示，制品发现裂纹可再转19次即要断裂，故应立即更换。

4.计算大尺寸或大体积制品的疲劳极限

由于塑件体积增大，局部区域出现残余应力及缺陷的可能性增大，因此用常规的S-N曲线查到的疲劳极限数据需要修正，可用下面的经验公式进行计算。

S_r=S₀（V/V₀）-0.34

式中，S_r是修正后疲劳极限；S₀是原S-N曲线中的疲劳极限；V、V₀分别是塑件及试样的体积值。

通常，疲劳试验的试样尺寸如图6-16所示。

5.用经验数据作近似S-N曲线

作图步骤举例如下：

1）确定N=10⁷时的应力幅值σ_a，一般取拉伸强度的20%～40%或抗弯强度的10%～30%。

2）确定N=10³时的应力幅值σ′_a，一般取拉伸强度的70%～90%，或弯曲强度的80%。

3）用双对数坐标，N为横坐标，σ_a为纵坐标，分别求出N=10⁷、σ_a及N=10³，σ′_a的坐标点，连成直线，即为近似的S-N曲线。