蠕变回复及其应变特性研究：以PP塑料制品为例

当制品在使用中受到一段时间恒定作用力后，又在较长时间不受力时，或受到间隔较长的间歇应力作用时，这类制品会产生蠕变和蠕变回复双重应变，且每次蠕变回复后制品上还会残留一部分塑性应变。在受反复间歇应力作用时每次残留应变会叠加起来，累积成剩余应变。剩余应变值比在持续应力作用下的应变值小，设计时可考虑相应地减小制品承载面积等结构参数。

为了便于剩余应变的计算，采用了如下简化方法。图5-30所示为经简化后的间歇应力下的蠕变回复曲线。

图中的T为加载持续时间，t为循环周期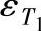，为首次加载后产生的最大应变，经T时间后卸载经t时间后第一次回复残余应变为ε₁。当第二次加载时，假设负载、持续时间、间歇时间与第一次相同，则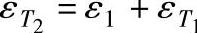，第二次卸载后残余应变为ε₁+ε₂；当N次循环后，N+1次加载时加载后的应变值应为N次循环后累计剩余应变值ε_N，加N+1次加载后的应变值ε_T即为ε_（N+1）=ε_N+ε_T。ε_N值的近似式计算式为

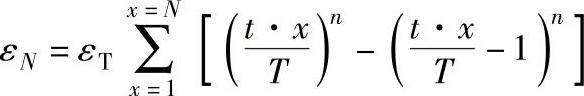
式中，ε_N是累计残余应变值；ε_T是每次加载T时间后产生的最大应变值（可从蠕变曲线查得）；t是每次循环周期时间；T是每次加载时间；x是循环次数；n是蠕变指数，ε=Atⁿ，可从蠕变曲线求得。

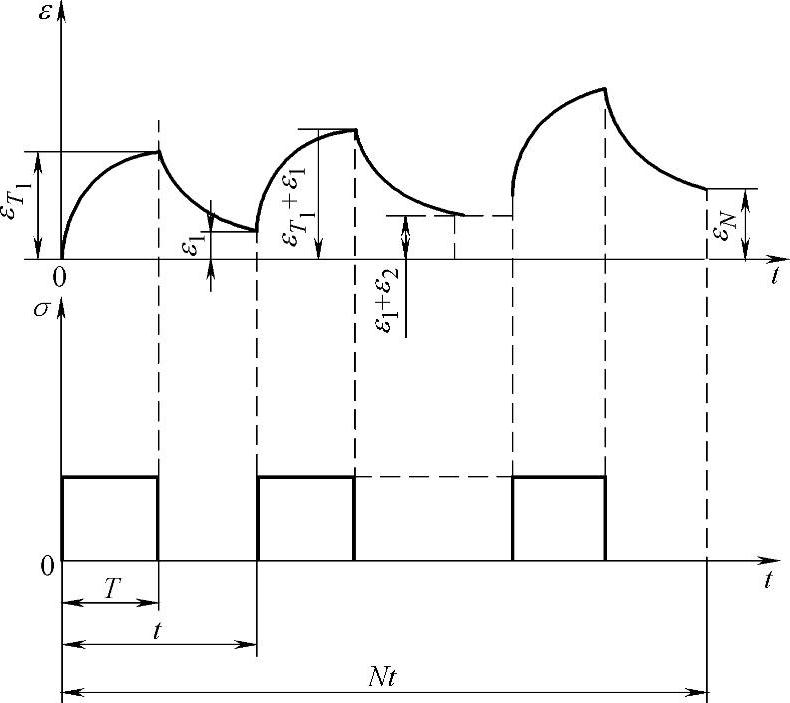
图5-30 简化蠕变回复曲线

注：假设每次负载、持续时间、间歇时间相同

例：PP塑料制品在9.8MPa应力下，承受加载100h、卸载100h的间歇应力作用，求经4循环周期后的剩余应变值。

解：1）计算蠕变指数n。从图5-17中查得PP塑料在9.8MPa应力下，10⁵s、10⁶s的时刻所对应的应变分别为2%和2.6%，代入蠕变指数式，即得2%=A（10⁵）ⁿ及2.6%=A（10⁶）ⁿ，两式相除，则得1.3=10ⁿ，对数值为n=lg（1.3/10）=0.11(www.xing528.com)

2）计算ε₁及ε₄。已知T=100h；t=200h；N=1、4；9.8MPa应力加载100h后ε₁₀₀=2.35%，将各数据代入即可求出下列各应变值：

第一周期回复应变值ε₁为

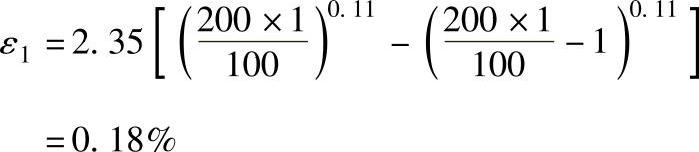
第四周期回复应变值ε₄

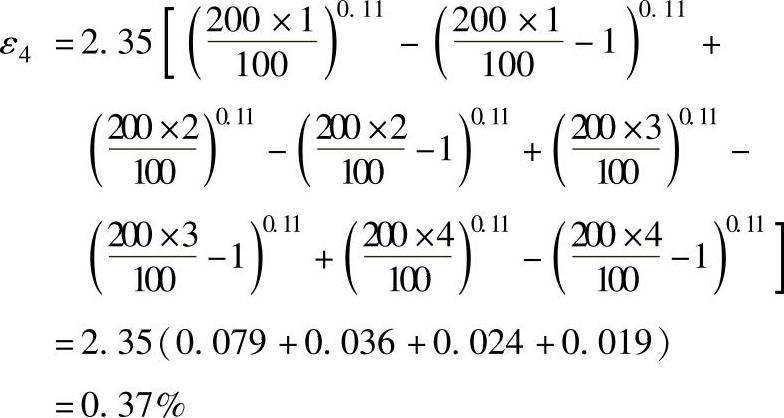
第五周期加载后累计应变值为

ε₅=ε₄+ε₁=0.37%+2.35%=2.72%

这种方法如用计算机编程，即可快速求解。