钎焊材料溶解点的探索与优化

激光软钎焊过程中，元件侧的金属化层以及PCB基板侧的焊盘会溶解到熔融钎料中。待焊材料的充足溶解对于清洁待焊表面和增加焊点强度至关重要。在传统软钎焊工艺中，待焊材料溶解厚度为几个甚至几十个微米，但在微电子组装中，焊盘或金属化层的厚度很薄。因此在钎焊过程中对于溶解的控制是非常必要的，过度的溶解会造成焊盘或金属化层脱落和失效。例如，在250℃条件下钎焊，6μm厚的Au薄膜会在1s内完全溶解到熔融共晶SnPb钎料中。温度越高，溶解速率越高。金属化层完全溶解的另一个危险是当钎料不能润湿下一层材料时出现反润湿现象。

激光软钎焊过程中，整个体系的温度和溶解速率不断改变，同时，钎料合金逐渐熔化，与焊盘的接触面积增加。随着焊盘或金属化层溶解的继续，熔融钎料中溶质原子持续增加，降低了溶解速率。以上因素使得激光软钎焊过程焊盘溶解的计算更加复杂。激光软钎焊非平衡温度场条件下焊盘向熔融钎料中的动态溶解，可以通过数值计算方法求解固-液质量传递动力学微分方程来获得^[29]。

溶解反应速率方程定义如下：

由于溶解量可以表述为

Q=ρ_sVC （12.6）

因此，式（12.5）可以描述为

式中，Q为溶解到液态钎料的总量；t为固-液接触时间；S为固-液接触面积；a为溶解速率系数；C_l为溶解极限；C为溶质原子在熔融钎料中的浓度；V为液态钎料的体积；ρ_s为液态钎料的密度。

当体积和温度为常数时，溶解方程可由式（12.5）给出：

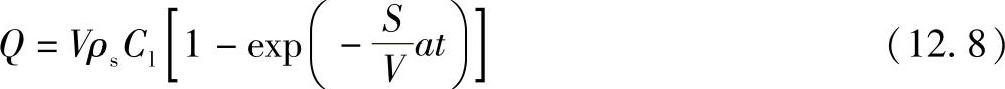
在激光软钎焊过程中，液态钎料的体积V、固-液接触面积S和溶解速率系数a随激光加热时间和温度而改变。因此，式（12.8）是一个关于溶质元素浓度的可变系数微分方程。

式（12.5）和式（12.6）进行离散后，可得：

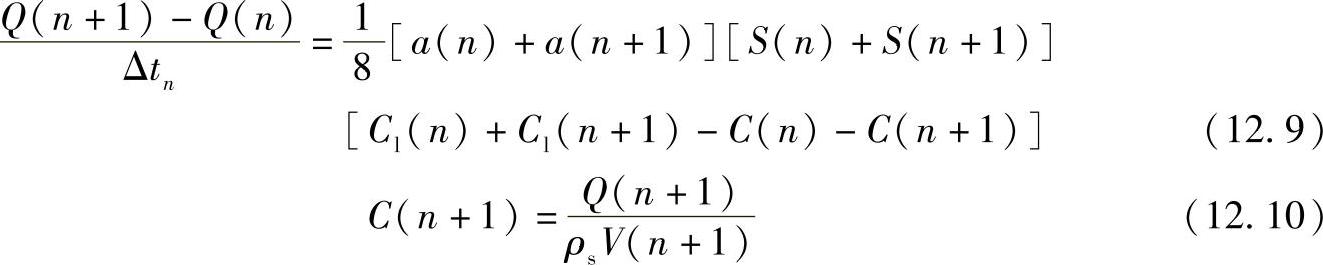(www.xing528.com)

式中，n为时间坐标；t为时间步。

将复杂的溶解微分方程被简化为简单的代数方程的求解。

假设：

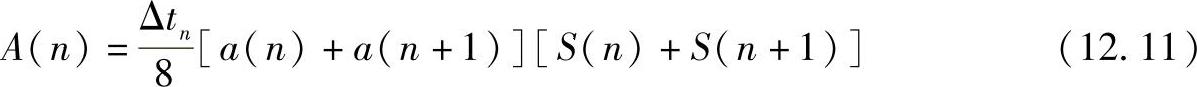
用式（12.10）替代式（12.9），则有：

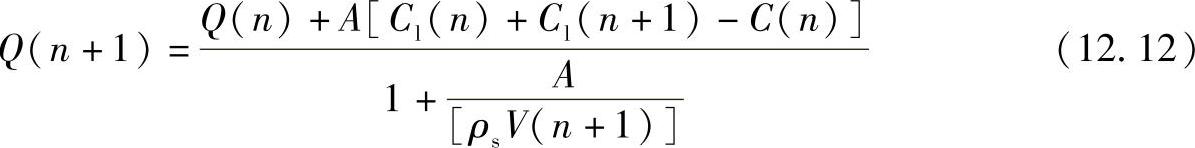
综合式（12.11）和式（12.12），可以获得非稳态温度场下溶解的数值计算结果。

图12.6为在温度场计算结果基础上^[29]，采用以上溶解微分方程计算获得的焊盘材料向钎料中溶解的动态曲线。陶瓷基板上焊盘材料为Ag厚膜导体，FR-4基板上焊盘材料为Cu厚膜导体。由于Cu和Ag在Sn中溶解极限的不同，因此在动态溶解过程中存在很大不同。Cu在Sn中溶解极限小，在加热过程中被饱和，溶解速率下降。但Ag在Sn中溶解速率较大，加热过程中溶解速率增加，溶解量也在不断增加。因此，在进行Ag厚膜导体钎焊时，应严格控制温度。

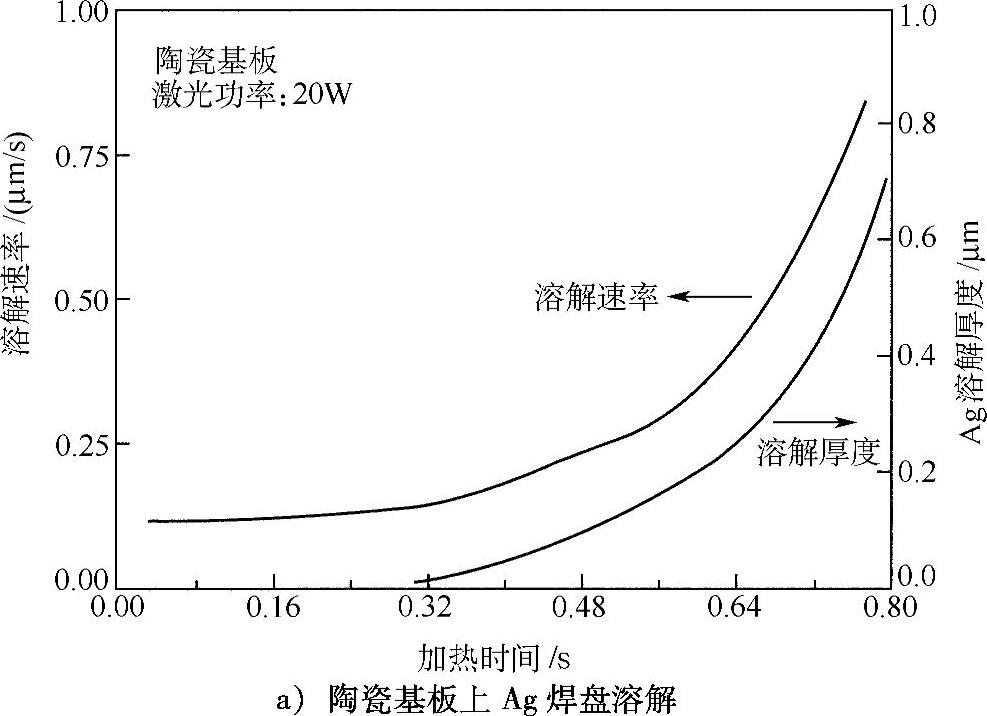
图12.6 数值计算获得的焊盘材料向共晶SnPb钎料中的动态溶解曲线

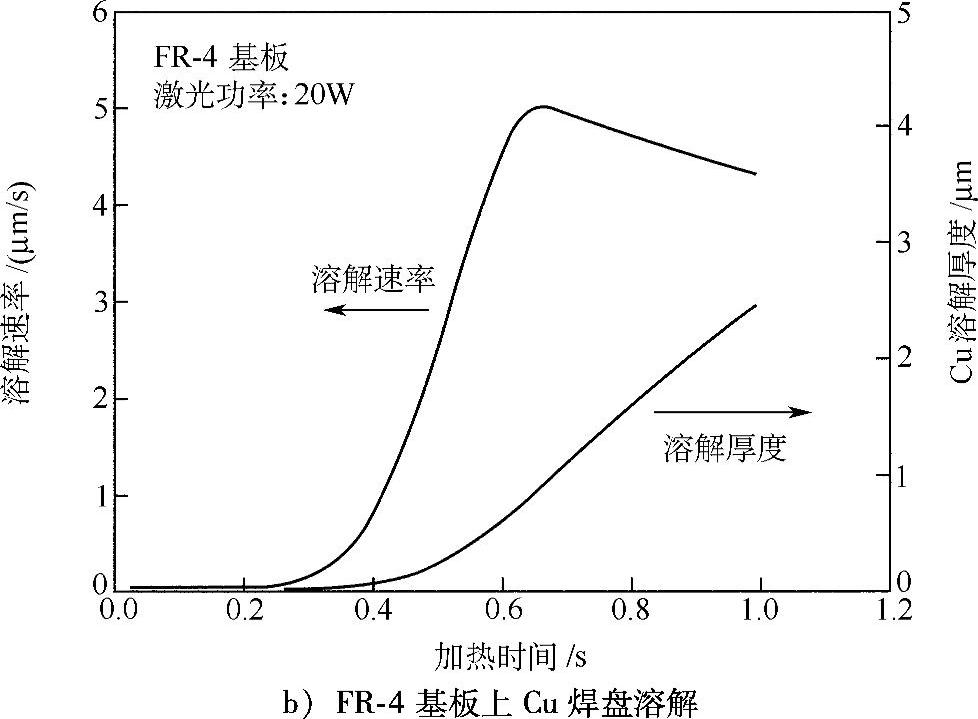
图12.6 数值计算获得的焊盘材料向共晶SnPb钎料中的动态溶解曲线（续）