Brockmann等人[20]采用数值方法研究了激光微连接金属薄板的温度场分布,如图5.1所示。金属薄板的厚度为h,以速度u移动的功率密度为W的激光束加热其上表面。当激光束的能量高于临界值Wcr时,金属薄板发生熔化。对于激光微焊接过程,熔化区域的尺寸很小(100~300μm),这意味着金属在表面张力的作用下保持水平,其焊接熔池表面的曲率可以忽略。等值线K是熔化区域的边界。
建立了描述上述问题传热过程的数学模型,并通过显式有限元方法进行数值求解。二维(薄板的厚度小于激光束的半径)和三维问题均可以考虑。
假设激光功率密度符合高斯分布模型,金属的熔化、蒸发和凝固、对流、辐射冷却以及物性随温度的变化均考虑进模型中。熔化金属的热导率高于实际值几倍,通过这种简单的处理可以考虑流体流动(Marangoni效应)对传热的影响。
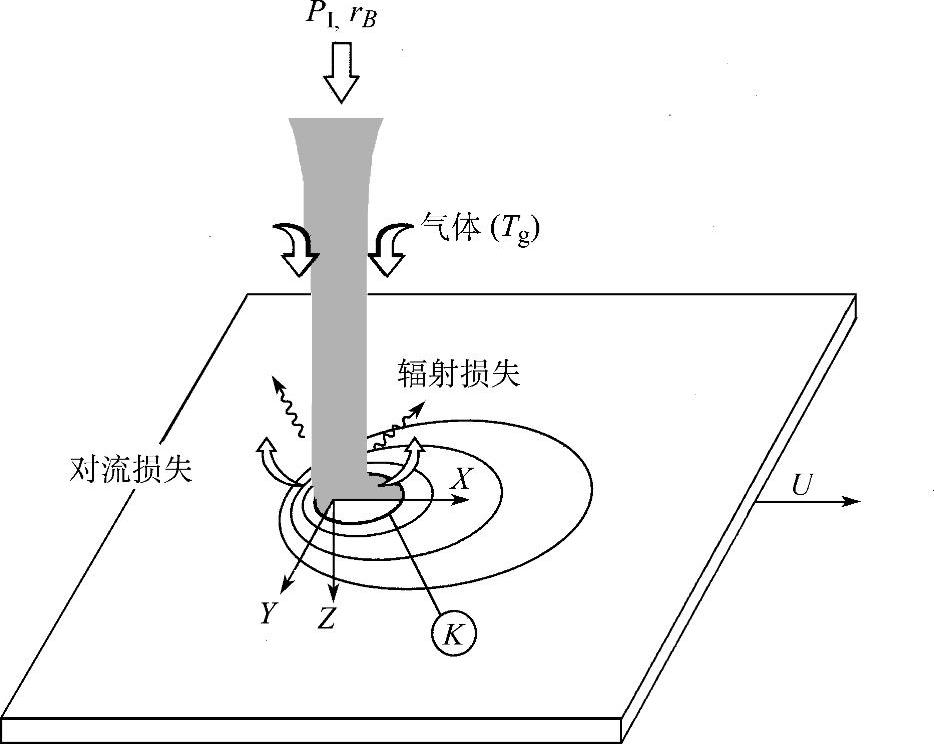
图5.1 激光加热移动薄板的原理图[20]
图5.2为是否考虑熔化时,计算所得不锈钢薄板的温度场差异。很明显,当考虑熔化时,熔化过程吸收潜热导致温度较低。
图5.3所示为计算得到的金属薄板下侧的温度分布。灰色区域的温度高于母材金属熔点,在这种情况下,熔化区域的尺寸X方向约为250μm,Y方向约为200μm,因此,可以形成完全熔透的焊缝。
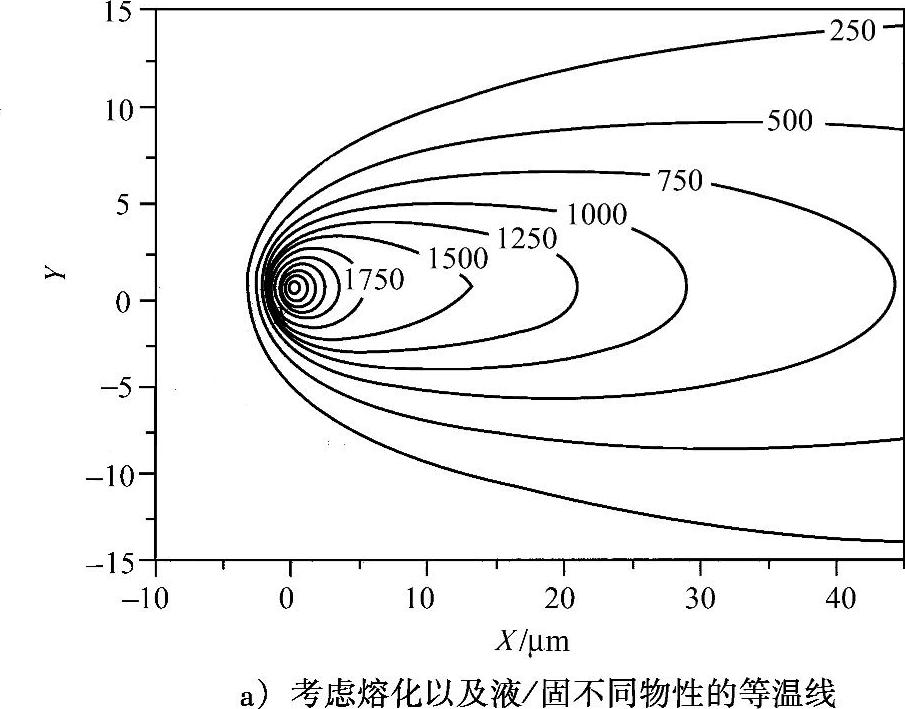
图5.2 是否考虑熔化时,不锈钢薄板的温度场差异(https://www.xing528.com)
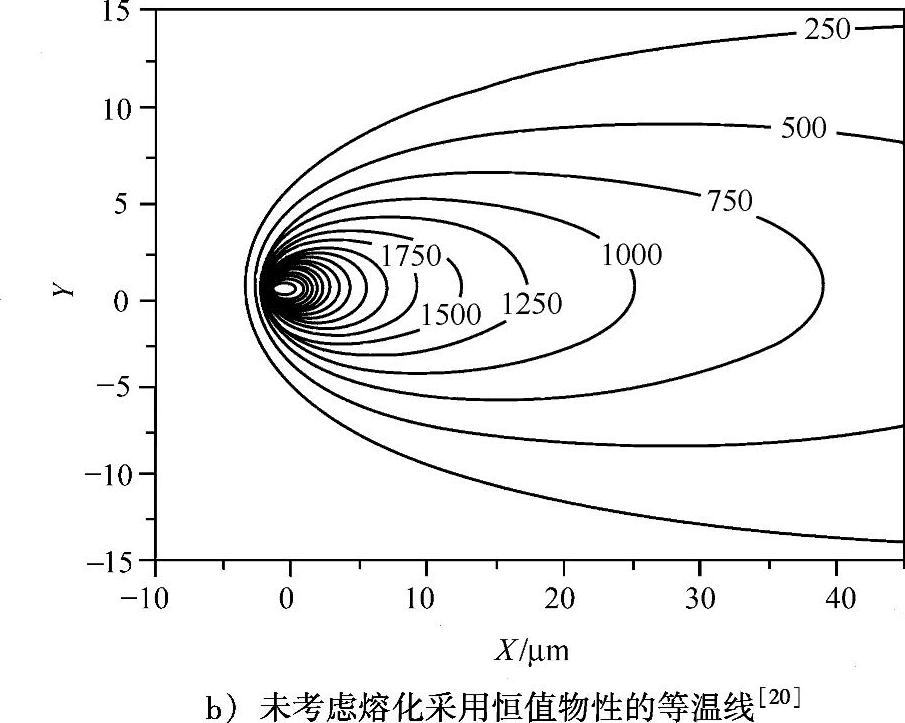
图5.2 是否考虑熔化时,不锈钢薄板的温度场差异(续)
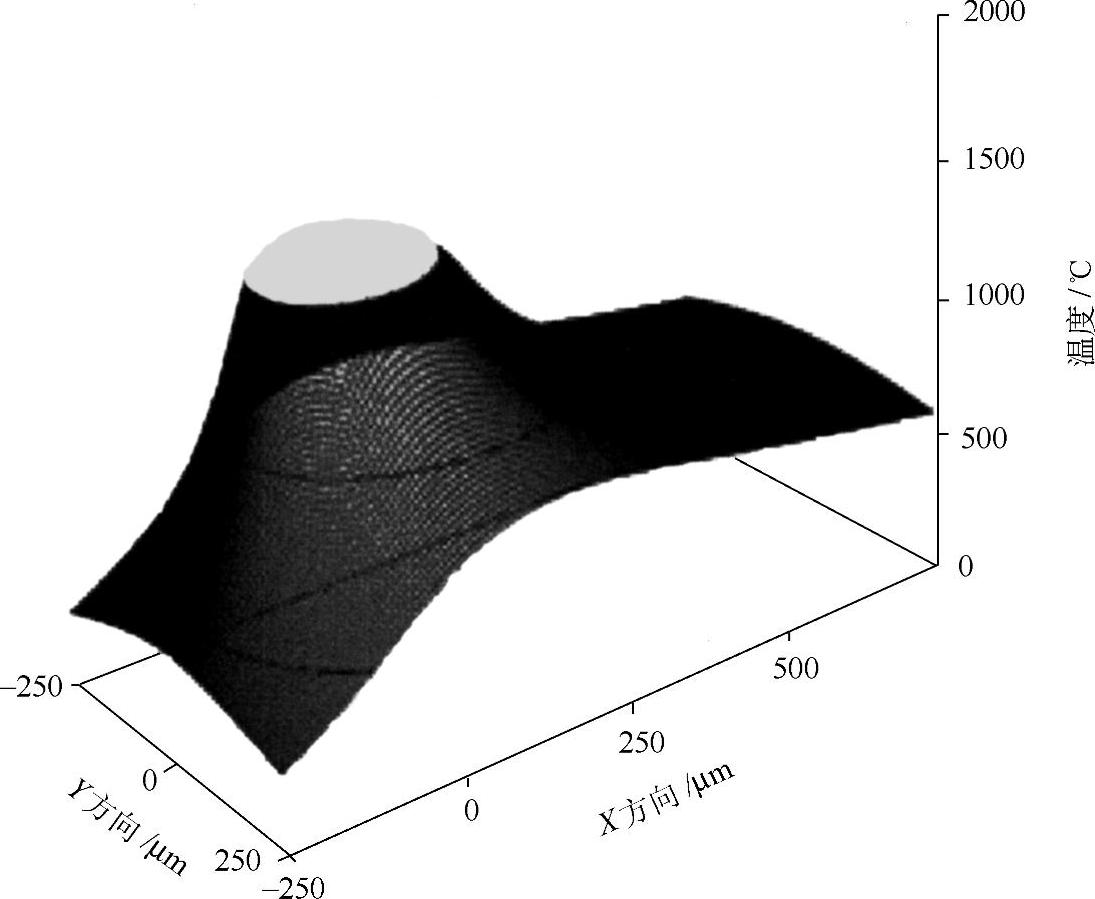
图5.3 计算得到的激光加热不锈钢板底侧温度分布(熔化区域为灰色)[20]
图5.4所示为计算得到的焊缝区截面的温度分布。可以看出计算结果与实际焊接吻合很好,焊缝的形状以及尺寸都与预测的熔化区域基本一致。
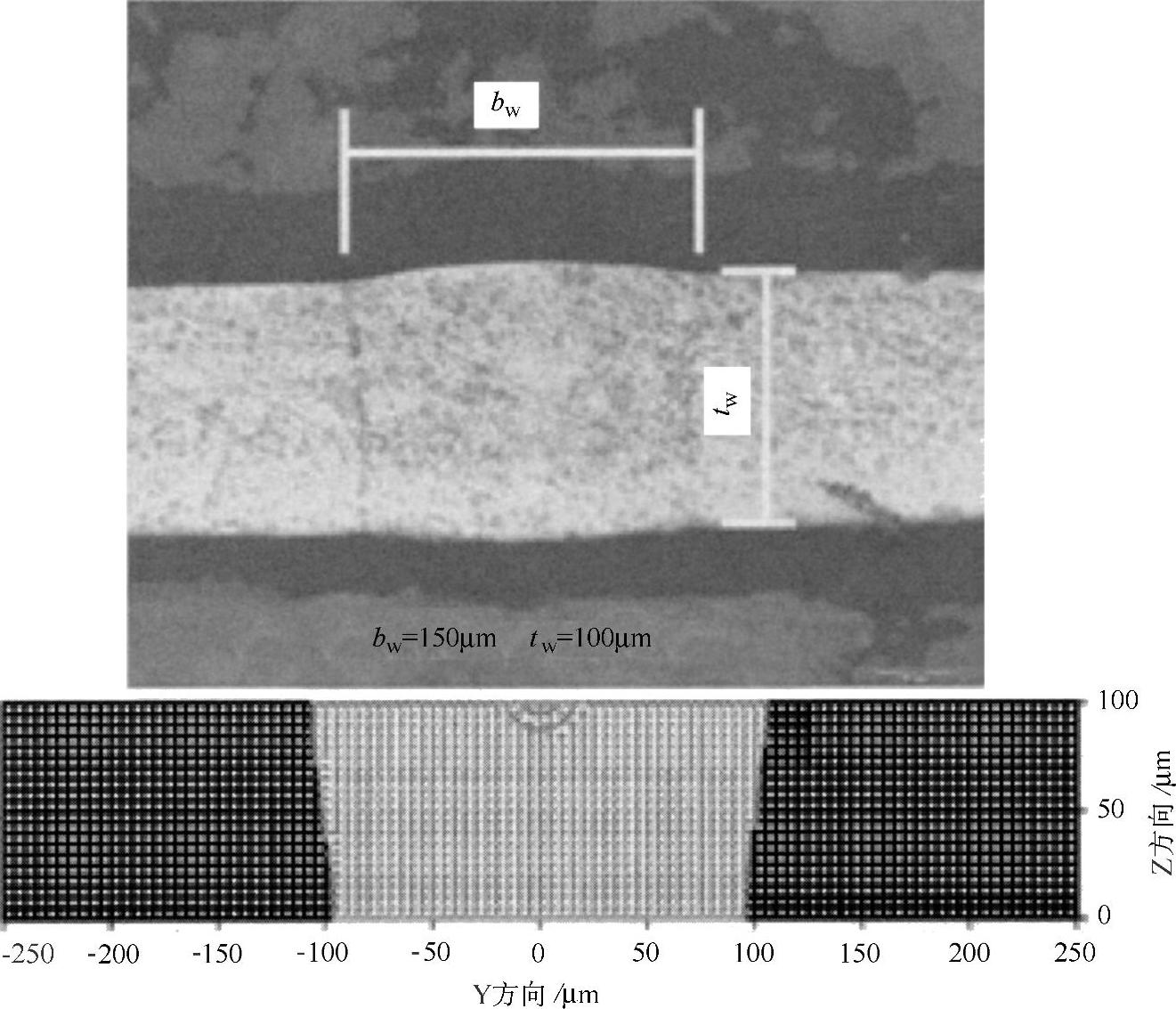
图5.4 计算得到的温度场以及相应焊缝横截面对比[20]
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




