数值模拟：搭接电阻焊的压缩和温度分布分析

通常，电导率随温度增加而减小，但接触电导随着温度增加而增加。键合初期（0～1ms），接触电阻比较高，此后随着接触面积的增加、温度的升高，接触电阻迅速减小；第二阶段（1～5ms），体电阻增加，样品被加热，开始发生塑性变形；第三阶段（5～7.8ms），压缩从20%增加到大约100%，如图4.20所示。体电阻与温度和几何尺寸有关，接触宽度与平板变形的增加导致体电阻减小。图4.20为模拟压缩和温度分布的结果。键合条件（U=0.7V，F=800N）下，压缩过程在t=7.5～7.8ms时结束。图4.20b所示为t=7.5ms时刻的变形情况以及温度分布。t=7.8ms时最高温度在（0.73～0.83）T_m之间，其中，T_m是SUS304的熔点（1723K）。压缩过程是在固相没有产生熔核的情况下发生的，与电极接触的顶部和下部变形较大，但由于接触电极冷却作用，不会发生熔化。压缩过程在t=7.8ms时结束，但此时键合中心区域的温度仍持续增加。对于t>7.8ms的情况，如果保持电压U=0.7V，中心区域将会产生熔核。该搭接电阻焊模型中并没有考虑熔化过程，如果预测挤压过程则需考虑键合区域的熔化。模型中上下电极的表面电动势分别为0.7V和0V。实际上，由于电极不是平的，弹性变形会导致表面电动势发生变化，因此，模拟搭接电阻焊过程比较困难。

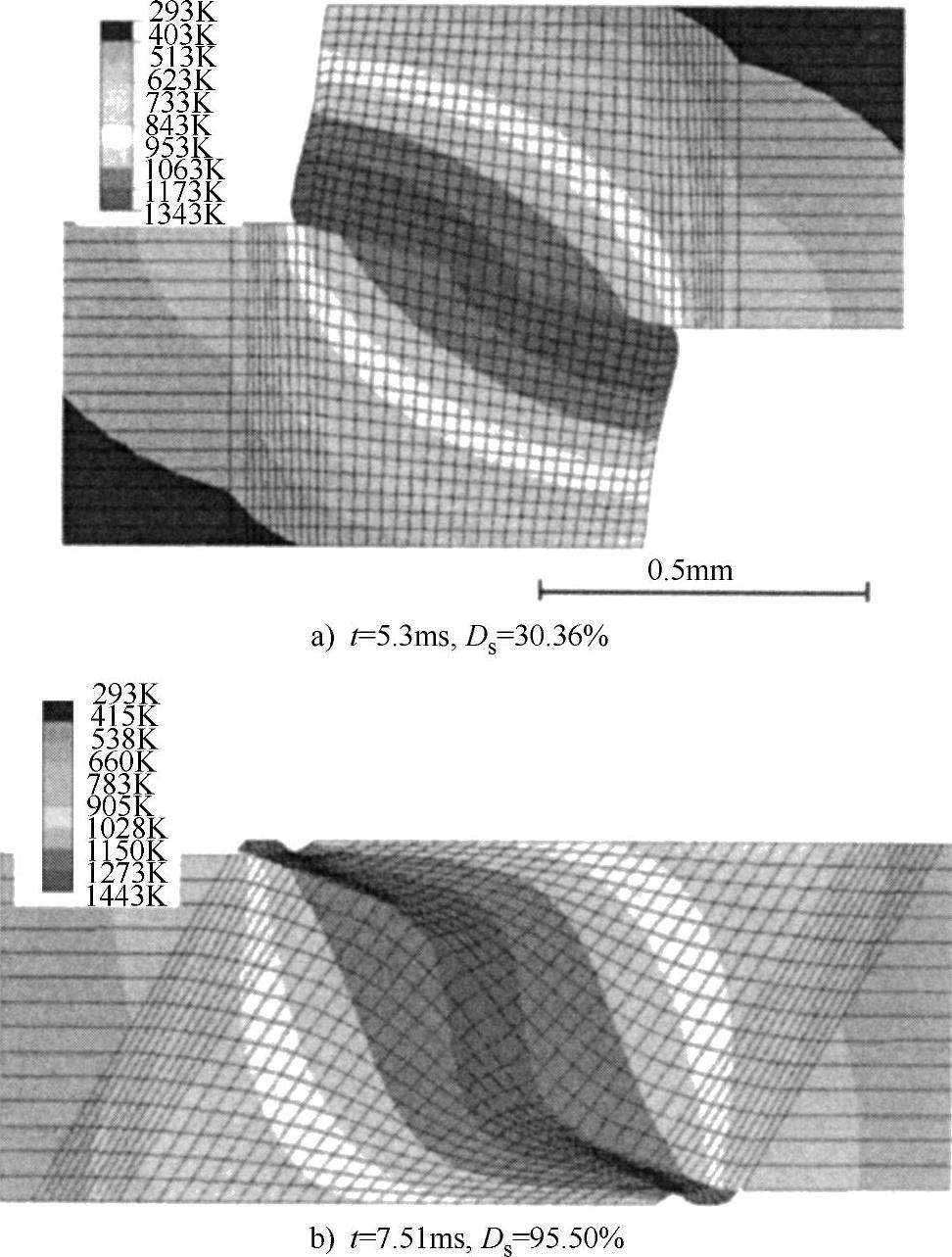
图4.20 搭接电阻焊的数值模拟结果(www.xing528.com)

（其中，D_s是压缩比，可以通过D_s=d_s/δ得到，其中，d_s是电极位移；δ是板厚）