界面微摩擦滑移的详细描述

假设超声振动的幅度为A_o，该值应该很小，以保证在时间增量Δt内，节点没有明显的滑移。例如，滑移模型处理微米或者纳米尺度的滑移时，其方向可以随超声振动迅速发生变化。当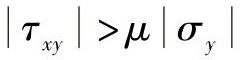，滑移方向可发生变化，其中，μ是滑移系数；τxy是切应力；σ_y是图4.16中y方向的应力。通过自洽的方法求解每一步的滑移率较难，假设微滑移率为，其中，α_s是常数，则通过微摩擦滑移可以求得下一时间步的应力分布，但由于每一步都有应力释放，摩擦滑移模型不能用于大的滑移行为。

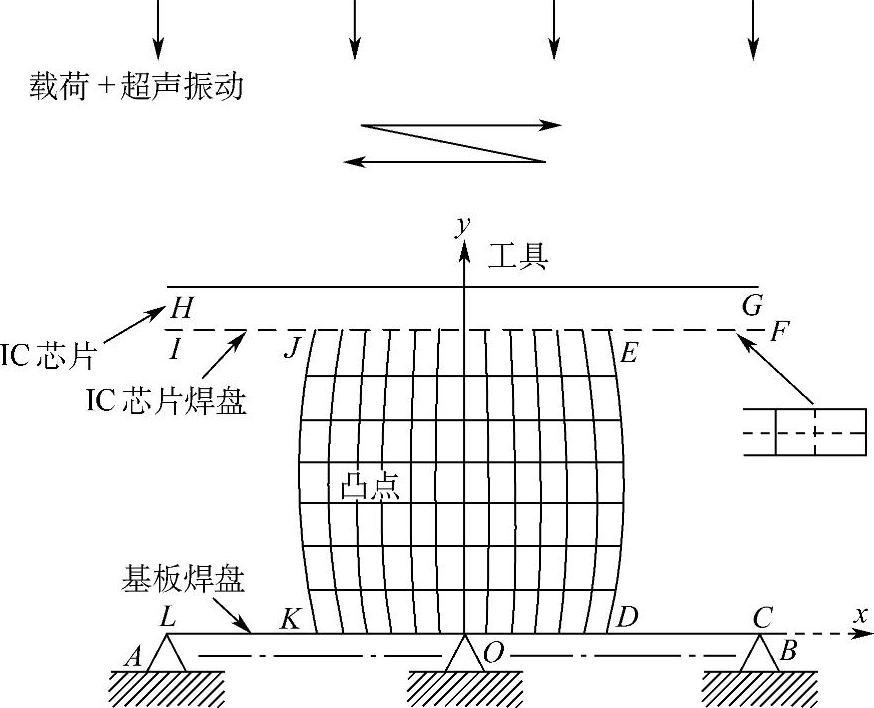
图4.16 键合凸点有限元网格划分示意图

摩擦滑移系数可以表示为以下三项的函数：μ_o、滑移量及加工硬化的和：

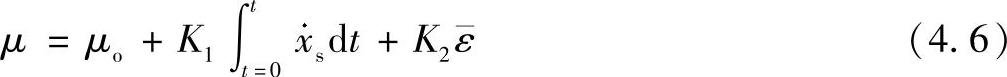(www.xing528.com)

式中，μ_o取决于局部法向应力P_l和温度T，可以近似写为μ_o=k_s（a_sP_l+b_s）（A_sT+B_s），且k_s可以表示为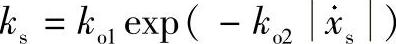+k_o3、k_o1、k_o2，其中，k_o3、a_s、b_s、As和B_s是常数，如表4.2所示。例如，P_l=392MPa，T=473K，t=0s时，μ=3.47×10^-1。滑移方向就是切应力的方向。当超声振动平行于IC芯片和凸点时，键合界面边缘处应力σ_y是正的（拉应力），与超声振动的方向相反。此时节点应该分离，但是超声振动下节点的分离过程是很难通过编程实现的，因此，假设当σ_y>0时，键合界面处节点不是分开的，具有相同的滑移率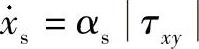（局部键合界面最内侧节点的滑移率，其σ_y=0）。这是模拟超声凸点键合过程仍然存在的一个问题。图4.16b中平行于IC芯片和表面HG的超声振动为u_v=A_osinwt，速率为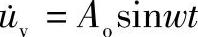，其中，A_o是振幅；w=2πf_v；f_v是超声振动的频率。时间增量Δt设置为Δt=T_v/8，其中，T_v是周期（T_vf_v=1）。

表4.2 微滑移模型中的常数

注：这些常数适用于Au/Au键合界面。