丝球焊的M值和引线与焊盘应力分布影响分析

丝球焊是一种重要的微连接技术，尽管目前还没有清楚地了解其连接机理，如丝球焊过程中的滑移和折叠机制。随着键合载荷的增加（或者高温下键合丝快速变形），实际的热压键合或热超声键合通常为边缘键合；高压条件下，可以观察到环状键合，即仅在边缘处键合而中间区域未有连接。这是由键合载荷和超声振动相关的摩擦滑移行为所致（Lun et al，2005）。如果超声能量相对键合载荷较小，不会发生摩擦滑移，因此，对于没有超声的热压键合在丝接触到焊盘后，几乎不会发生滑移。Mayer等人（2000）发现金属间化合物从中心区域产生并向边缘扩展。摩擦滑移在Au球键合到Al焊盘过程中起着非常重要的作用。Lum等人（2005）认为金属间化合物在边缘处形成是由于随着超声能量的增加，环状微滑移转化为总体滑移，从而导致整体键合的形成。

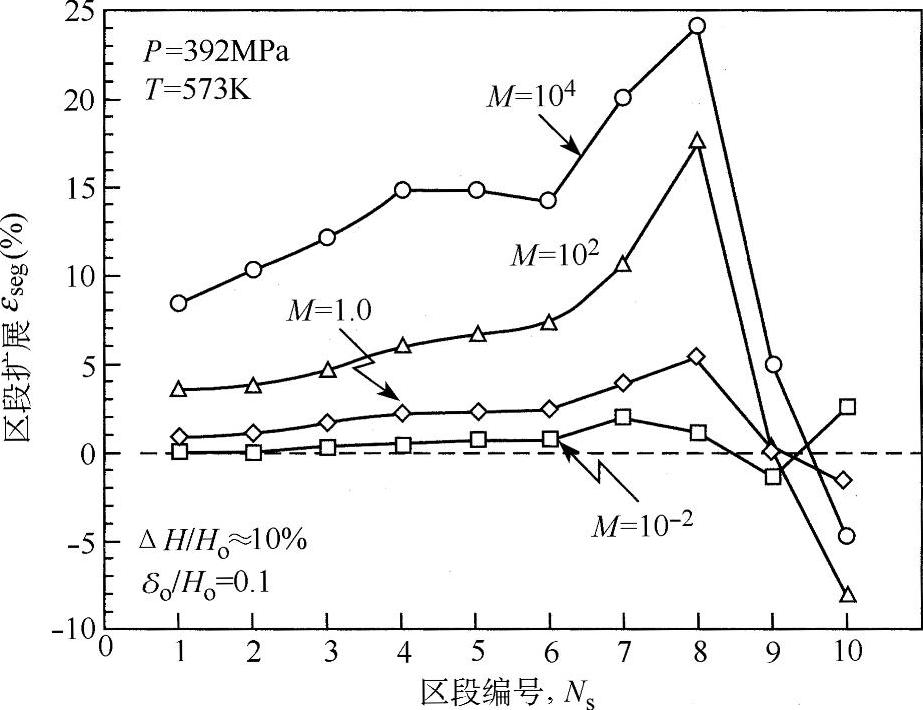
图4.6 M值对界面扩展的影响

图4.7 引线和焊盘截面的等效应力分布

由于微滑移与金属间化合物生长相互作用，准确地模拟实际的滑移行为非常困难。Liu等人（2004）模拟了热超声球焊过程，并且讨论了超声振动对于丝球焊键合的影响。结果表明，超声能量能够通过提高有效应力和丝的变形来提高应变速率。另一方面，由于楔焊中超声振动沿丝的纵方向施加，二维模拟很难实现。故本节主要研究没有超声振动的丝球焊模拟过程。

焊盘厚度也会影响热压丝球键合的过程（Ishizaka等，1977）。随焊盘厚度的增加，Au球与Al焊盘的中心区域发生键合的可能性增加。模拟中必须考虑焊盘厚度对于热压键合的影响。

1.模型和计算过程

Saeki等人（1991）采用刚塑性有限元的方法模拟了Au丝球与Al焊盘的键合过程。由于键合工具的毛细压力，Au球在键合过程中发生了很大的变形。在此，Saeki等人并没有从界面变形的角度给出形成边缘键合的原因。

Takashi和Inoue（2002）建立了一个简单的丝球焊模型来研究焊盘厚度对丝球键合的影响以及界面扩展对边缘键合行为的影响。以下从三个方面讨论：①尺寸比δ_o/H_o（扁平工具）或δ_o/H_o′（图4.8中的V形沟工具）；②式（4.3）中的M值，表达了丝和焊盘之间力学性能的差异；③工具形状的影响，这里δ_o是焊盘厚度，H_o是丝的初始高度（直径），H_o′是图4.8所示的高度。图4.8为丝和焊盘截面的网格划分。丝的初始直径为10μm。根据平面对称性（平面应变近似），仅对右侧截面进行了网格划分。在丝与焊盘或者工具表面接触之后，假设焊盘与丝界面或者丝与工具界面固定。区段扩展由式（4.4）定义。图4.9为区段编号定义，N_s1，N_s2，N_s3。

在丝球焊模型中，区段N_s1=1和N_s3=1～18是初始界面，区段N_s1≥2和N_s2≥2是初始条件下的表面。新的界面通过丝表面（N_s1=2～11）向焊盘表面（N_s2=2～11）折叠产生。图4.10为获得新节点的方法。当折叠发生时，有必要在有限元网格去除或者添加节点。图4.10中节点1是丝和焊盘界面上的节点，节点2是丝表面上的点，节点3和节点4是焊盘表面的点。初始网格如图4.9所示，变形后节点2′和节点3′几乎重合，如图4.10所示。如果节点2′和节点3′在全局坐标系中不相同，新的节点取节点2′和节点3′的中点。该方法避免了对所有节点重新进行网格划分以及关于位移率矢量和节点位置的数据传递，使得增加键合时间容易实现有限元求解。

计算需要一直重复，直至N_s1=11的丝表面折叠到N_s2=11的焊盘表面。关于丝球键合模型的研究很多（Takahashi等，1996；Takahashi和Inouse，2002），除了折叠处理外，其余与引线键合相同。丝单位长度上的载荷W_b定义为P×d，其中，P是键合压力；d是丝的初始直径。初始阶段，恒定的力作用在图4.8a所示的区段上。接着在每个计算步内（时间t）采用微扰的方法，通过使工具界面的节点力总和等于载荷W_b，

将节点位移率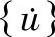}转换成实际的率矢量。求解每个时间步内真实的位移率矢量后，便可得到t时刻各个节点正确的位移率矢量（，），其中（x，y）为节点坐标。可以通过时刻的（x，y）来更新t=t+Δt时刻的坐标（x，y）。判断两种折叠情况，网格重划分、更新边界条件后进行下一个时间步（t=t+Δt）的计算。当丝压缩率ΔH/H_o或者ΔH′/H_o高于50%，或者丝的表面区段N_s1=11折叠到焊盘表面时，便可获得计算中止时间t_end。丝的压缩率如图4.11所示。丝的压缩率ΔH′/H_o′主要用于V形沟工具的丝球焊过程。由于没有施加超声，热压键合模中，压力P和键合温度T比实际热超声键合高。例如，对于扁平工具P=980MPa，V形沟工具P=1568MPa，

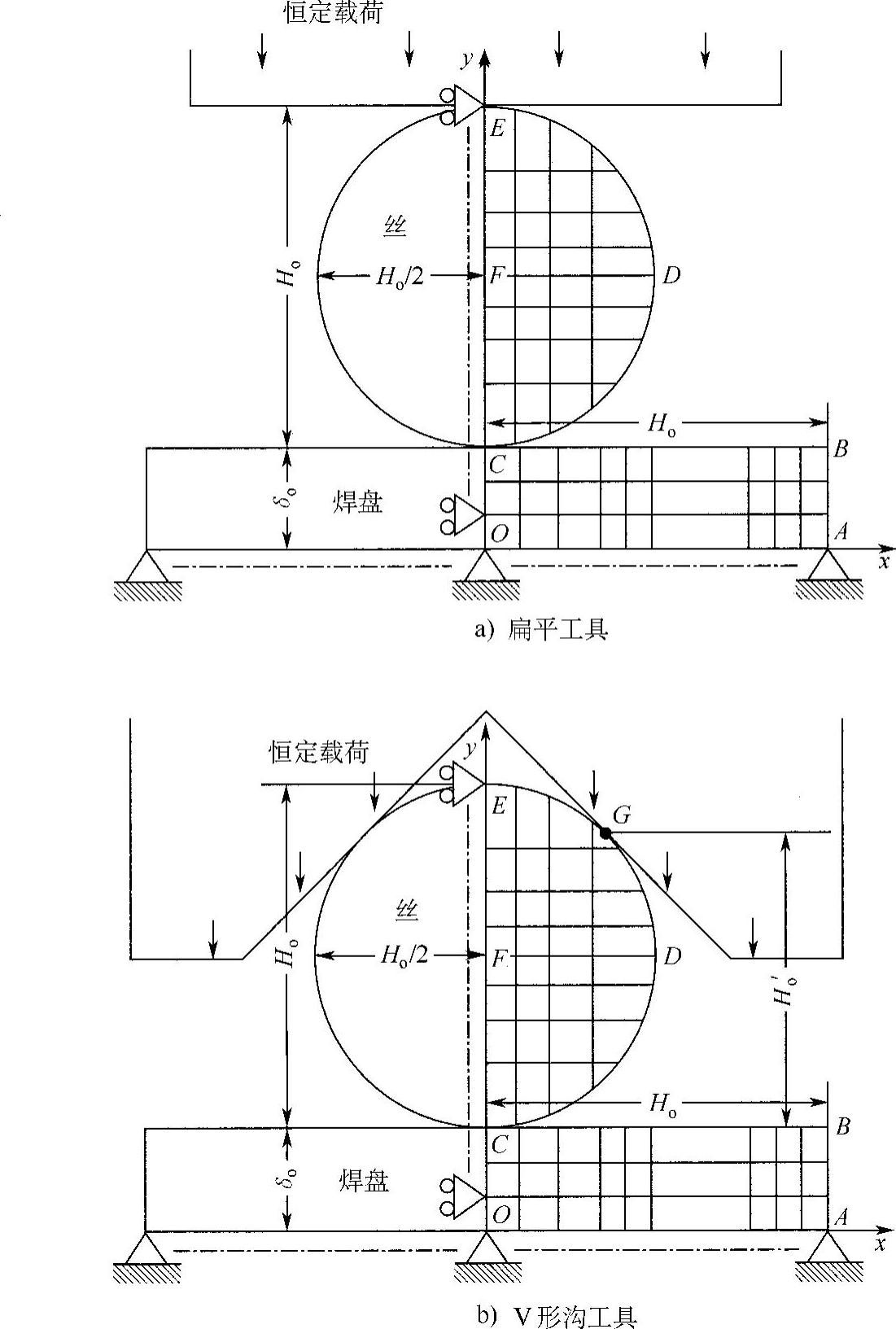
图4.8 引线和焊盘截面的网格划分

对于容易变形的丝的指定温度T=573K。

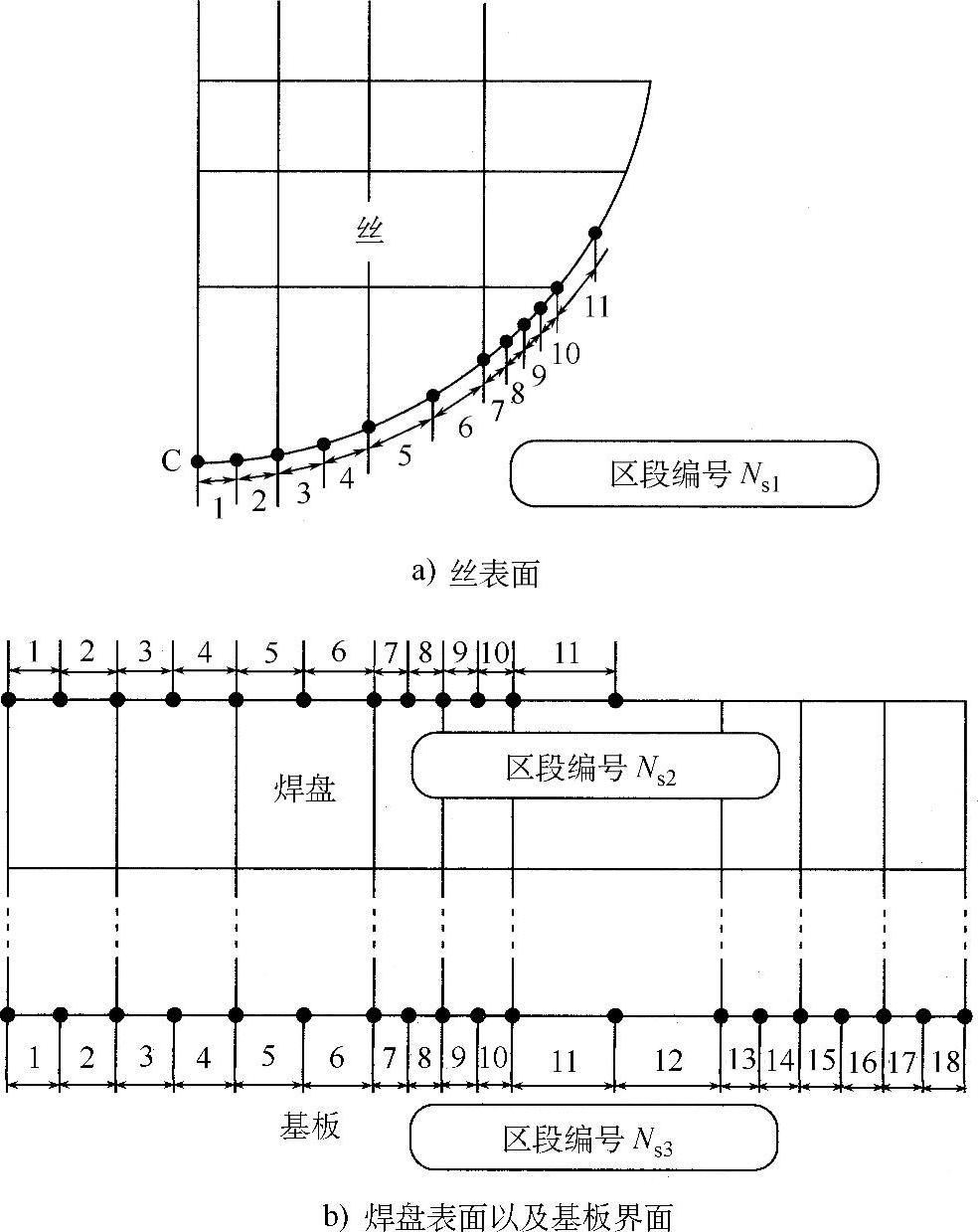
图4.9 区段编号定义

2.数值模拟(www.xing528.com)

基板对焊盘的约束效果随尺寸比的增加而减小。当尺寸比δ_o/H_o增加时，焊盘容易变形，被丝压出凹痕。如果焊盘很薄（M=1，δ_o/H_o足够小），折叠后等效应力集中在丝的两个边缘内侧，但是中心区域应力不够大，不会造成该区域的界面变形。另一方面，如果尺寸比δ_o/H_o足够大，应力在中心区域和边缘区域都会变高（Takahashi和Inoue，2002）。由此可知，随焊盘厚度的增加，键合中心区域的界面扩展增加。

尺寸比也会影响丝球焊过程中的界面扩展。随着尺寸比δ_o/H_o增加，中心区域的界面扩展增加。如果焊盘很薄，即使丝的表面变形向外扩展，焊盘表面边缘处仍为负扩展（压缩）。

焊盘硬度对于理解界面变形行为有重要影响。随着焊盘变硬或者M值增加，丝的压缩率减小。这是由于硬的焊盘对丝的约束作用，变形需要更大的流动应力。M值对焊盘和基板之间的界面应力分布也有影响，应力随区段编号N_s3的变化而变化。如果焊盘非常薄且M<1，应力集中于丝的边缘，就易形成边缘键合。

图4.10 丝表面向焊盘表面的折叠过程

（黑色圆圈是节点。节点1是丝和焊盘的交点，节点2在丝表面上，节点3和节点4在焊盘表面。白色的点1′、2′、3′、4′是在给定的合适时间增量Δt下，点1、2、3、4的新位置。点2′和点3′的折叠通过读取坐标来判断。如果点2′向点3′折叠，丝和焊盘之间需要添加新的公共节点）

图4.11 丝的压缩率定义

随着丝的直径从10_μm增加到500μm，在相同的尺寸比（δ_o/H_o=1）条件下，焊盘厚度δ_o从1_μm增加到50μm。在实际的Al丝球焊中，即使丝的直径为300μm，焊盘的厚度也就几个_μm，由此可知，应力集中出现在基板上，从而更容易损伤基板或者IC芯片。如果焊盘由于沉淀硬化就容易发生损坏（Onuki和Koizumi，1996）。带有超声振动的载荷控制对于薄而硬的焊盘中心区域形成键合很有利，如滑移和重叠机制非常重要。

图4.12和图4.13所示为丝和焊盘变形过程的数值模拟过程，图的右半部分为有限元网格，左半部分是每个节点的位移率矢量。图4.12对应扁平工具，图4.13对应V形沟工具。假如丝和焊盘的材料为Au，丝的初始直径为10μm，则M=1。图4.12中每个图顶部的数值代表该处y方向的位移率矢量。图4.13左半部分的值为与V形沟工具第一接触点G的位移率。在扁平工具作用下，丝的中心发生比较大的压缩变形；在V形沟工具的作用下，丝的压缩不是很显著，而且丝的高度H_o变化也不是很大。这是由于丝的上侧被挤入丝与V形沟工具上部缝隙的缘故。V形沟工具的约束明显改变了丝的变形形状，减小了变形率。

图4.12 扁平工具的数值计算结果（P=980MPa，T=573K）

图4.13 V形沟工具的数值计算结果（P=1568MPa，T=573K）

图4.14所示为各个区段的区段扩展，表明如果ΔH′/H_o′保持在36%，V形沟工具更有利于界面扩展。由于V形沟工具键合界面中心区域的界面扩展更大，所以V形沟工具比扁平工具更容易实现中心键合。由图4.14b中可以观察到在焊盘边缘区段N_s2=9～11呈现负扩展。这表明侧表面的折叠过程包含丝表面的扩展以及焊盘边缘区域的收缩，其折叠行为非常复杂。

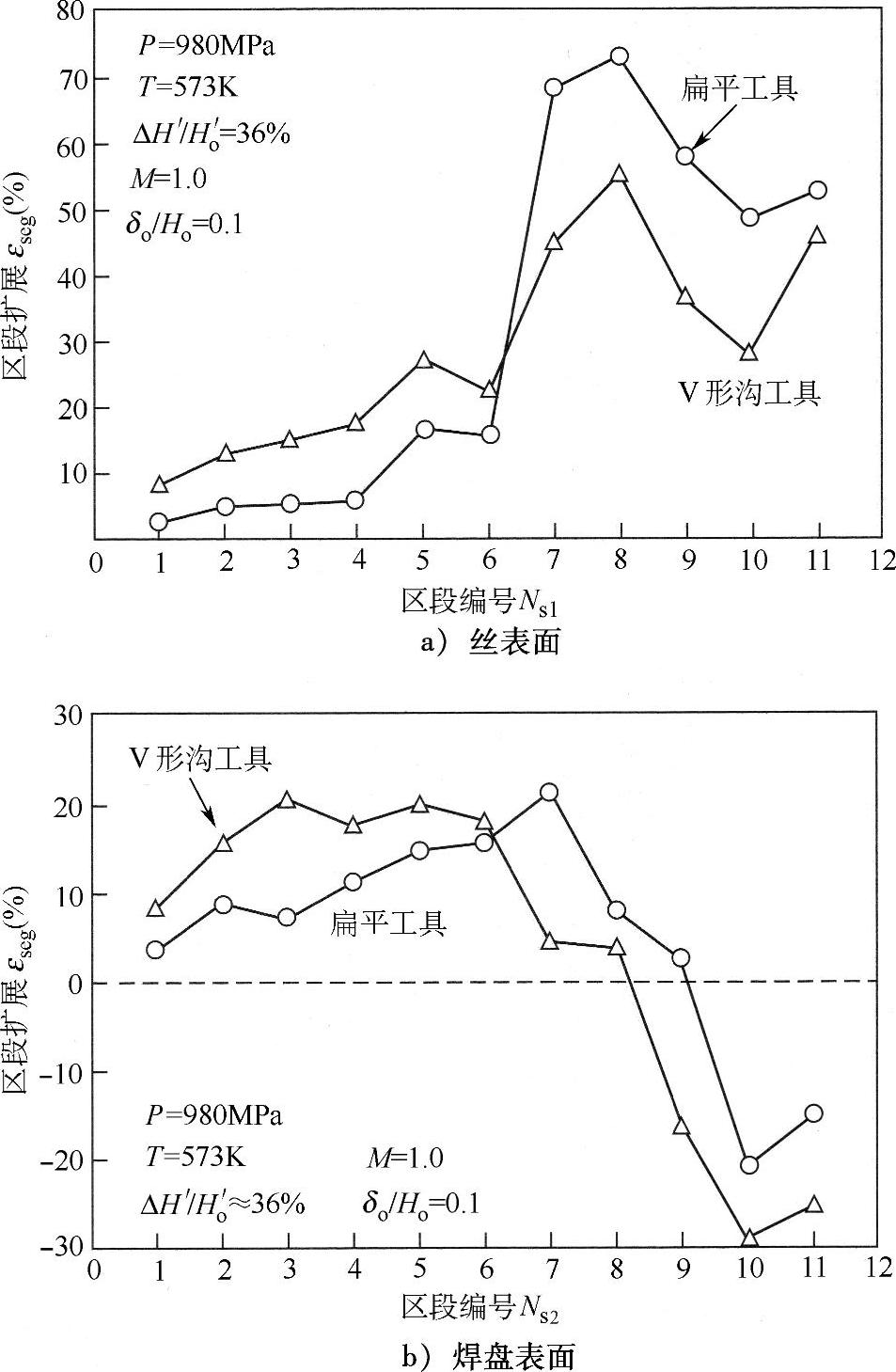
图4.14 工具形状对界面扩展的影响