TAB内引线键合的分析介绍

1.模拟及计算过程

TAB是集成电路封装中一种有用的互连方法。TAB内引线键合是指载带上细的引线与集成电路焊盘的键合过程。TAB时，镀金细引线与镀金凸点或者Al焊盘键合。模拟中引线键合可以简化为如图4.1所示的模型，图4.1a是简化模型，图4.1b是截面Q的有限元网格。引线及焊盘均由金组成。模拟中假设工具界面FE和键合界面GD固定在引线和界面之间，基板OB和键合工具FE很硬不会发生变形。引线和焊盘的温度保持在573K。这是M=1的情况，参数M定义为

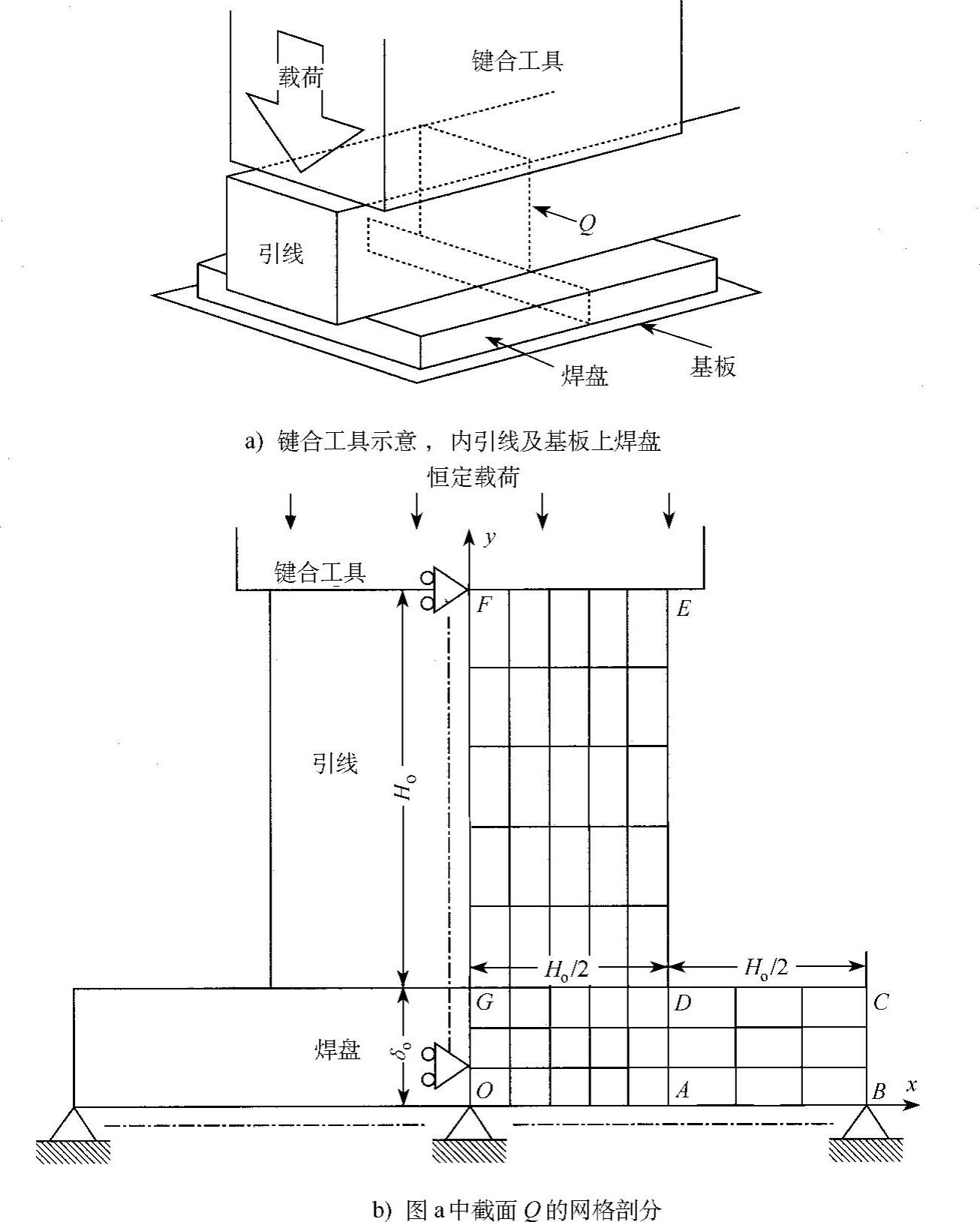
图4.1 内引线键合的简单模型

式中，A_op和A_oL是焊盘和引线的无量纲参数；Q_p和Q_L是粘塑性变形的激活能；T_p和T_L是引线和焊盘的平均温度。参数M在讨论与焊盘和引线之间温度差相关的材料力学性能的影响时很有用（Takahashi等，1996b）。尺寸比定义为δ_o/H_o，其中，H_o是引线的初始高度，δ_o是焊盘的初始厚度，如图4.1b所示。引线的压缩比定义为ΔH/H_o，这里ΔH=H_o-H，H是键合后的高度。图4.2a为引线和焊盘界面处的网格及节点信息，图4.2b定义的区段扩展ε_seg如下

图4.2 引线和焊盘键合示意

式中，l_o是相邻网格节点之间的初始区段长度；l是变形后的区段长度。区段扩展在有限元模拟里意味着局部的界面变形。局部界面扩展是控制压力键合强度的一个主要因素，如没有超声振动的固相微连接。界面扩展是与金属表面之间固相压力焊的程度Ψ密切相关的，可以表述为

式中，G_d（0～1）是表面污染物或者氧化物薄膜的延展率（Zhang和Bay，1997）。区段扩展是影响键合的一个重要参数。

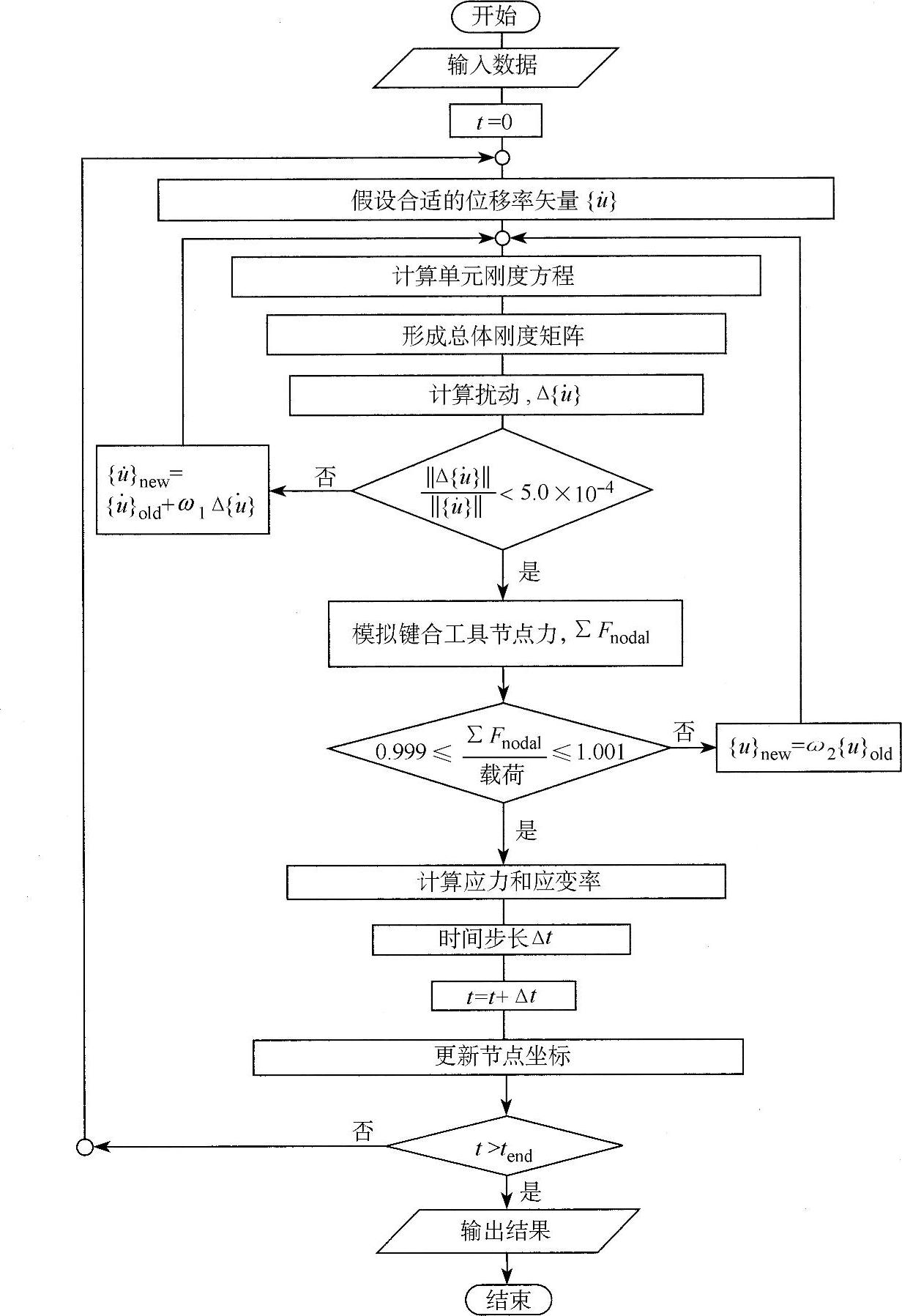
图4.3是计算程序流程图。首先，所有节点需要指定合适的位移率作为初始位移率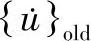。边界条件为键合工具在y方向上对工具界面FE施加的键合载荷W_b（引线单位长度的载荷），如图4.1b所示的y方向工具界面FE处节点力总和。y方向工具界面FE处还需要指定某一位移率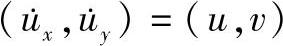作为初始值，且υ在每一计算步内保持不变。由于工具界面不发生滑移，故u=0。图4.1b为固定界面OB处边界条件指定位移率υ=0。合适的位移率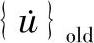在微扰方法（Takahashietal，1993）的每个计算步中应该收敛到新的位移率向量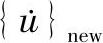。y方向工具表面FE处的节点力的总和∑F_nodal，在计算过程中通常不等于初始阶段的边界载荷W_b。实际上节点力总和∑F_nodal必须等于边界载荷W_b，也就是说，必须改变界面处位移率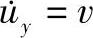，使其节点力总和∑F_nodal等于边界载荷W_b。数值求解过程通过迭代收敛使其微扰。在

(www.xing528.com)

图4.3 计算程序流程图

每个循环中，∑F_nodal最终等于边界载荷W_b。时间步Δt通常在10^-10～10^-2s之间。如果∑F_nodal<W_b，系数w₂>1。当前模拟中，系数w₁位于0.1～0.3之间（尽管其通常大于1）。键合压力定义为P=W_b/w，这里w为引线的初始宽度。

2.数值模拟

图4.4为计算的焊盘厚度对界面扩展的影响。由于采用有限元方法，界面扩展用图4.2b所示的区段扩展ε_seg和区段编号来表示。如图4.4所示，当δ_o/H_o=1时，界面扩展主要发生在键合界面的中心区域。随着δ_o/H_o减小，界面扩展也变小。ε_seg最大出现在N_s=8时，最小值出现在键合界面的边缘（N_s=9和N_s=10时），例如，当焊盘足够薄时，边缘趋于收缩，这是焊盘和硬基板的约束效果。区段扩展的峰值出现在边缘以内，对于ΔH/H_o=10%，εseg在N_s=8处达到5%，即使对于δ_o/H_o=0.1也是如此。这表明引线边缘以内更容易键合。

粘塑性变形通常受式（4.2）（Takanashi等，1999a）所示的等效应力所控制。

图4.5所示为图4.1a中截面Q上的等效应力分布，等效应力受焊盘厚度（尺寸比δ_o/H_o）的影响，其在引线中心以及焊盘和引线界面的边缘处最大。当δ_o/H_o足够大时，如图4.5a所示，边缘处的应力分散进入焊盘内部，基板上不存在集中的载荷；随着焊盘尺寸的减小，应力集中在引线的边缘，容易引起基板损伤。

图4.6所示为M值对界面扩展的影响。如果引线的温度T_L=573K，M=10^-2时焊盘的温度T_P=491K；当M=1时，T_P=573K；当M=10²时，T_P=678K；当M=10⁴时，T_P=740K。如图4.6所示，当M=10^-2时，没有发生界面扩展。这表明直接无凸点引线键合很难用于硬金属（硬基板上的薄冷焊盘）。然而，随M值的增加，即焊盘被加热，引线/焊盘界面开始变得容易发生变形。当M≥10²时，尽管ΔH/H₀=10%，N_s在7～8之间，区段扩展仍高于10%。N_s在9～10之间时，区段扩展减小，引线边缘处界面被压缩。即使M值增加，由于焊盘的鼓起，引线边缘处的键合界面也趋向于收缩。这种鼓起变形在加热焊盘变软的情况下变得更显著。

图4.4 δ_o/H_o对界面扩展的影响

然而，界面扩展是非均匀的且在引线边缘收缩。图4.7为引线和焊盘截面的等效应力分布。当焊盘温度很低时（M=10^-2），等效应力集中在引线内十字形处（如图4.7a所示）以及引线两侧的焊盘处。图4.7b所示，当M=10⁴时，图中黑色区域（σ->300MPa），大面积地分布在引线内部。由于焊盘加热后变软，焊盘内部的流动应力比引线内部低很多，故焊盘比引线容易变形且在引线边缘鼓起。即使焊盘中的等效应力低于引线中等效应力，引线和焊盘之间的力也能相互平衡掉（y方向）。数值计算可以准确地预测焊盘厚度和材料力学物性的影响（Takahashi et al，1999b）。

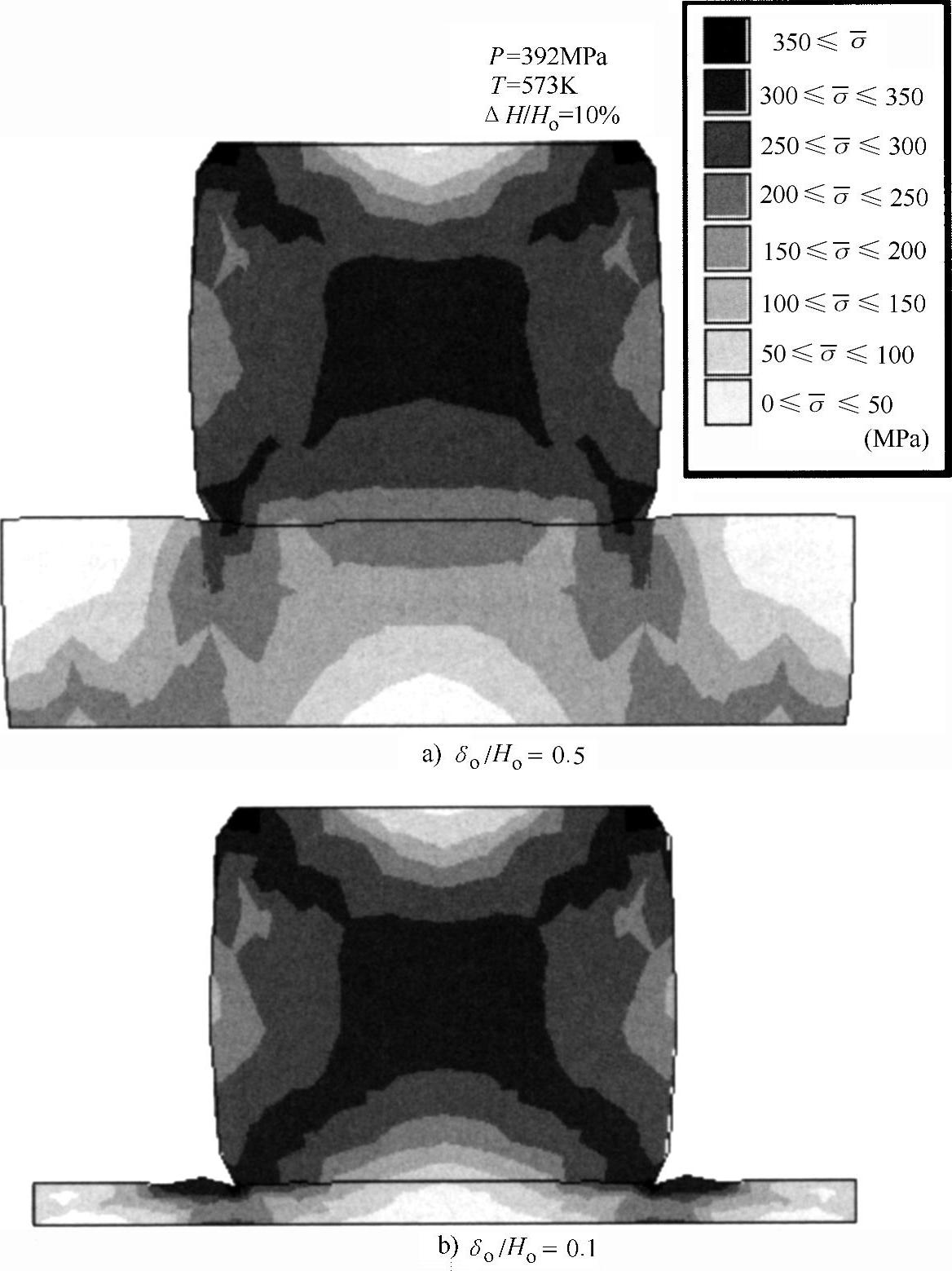
图4.5 引线和焊盘截面的应力分布