【摘要】：速率敏感类材料如金、铜以及铝等发生粘塑性变形时，其流动应力取决于应变速率。有限元方法可以模拟两个不平整键合表面的接触过程，以及由于粘塑性变形引起的孔洞收缩。界面变形与接触面积的增加显著相关。理解随时间变化的塑性变形对于模拟微连接过程的界面变形非常重要。
速率敏感类材料如金、铜以及铝等发生粘塑性变形时，其流动应力取决于应变速率。当材料被加热时，即可观察到材料的粘塑性行为。稳态等效应变率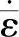
可以表示为
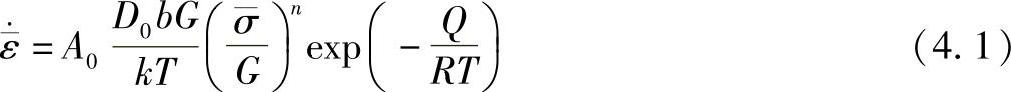
式中，A0是无量纲常数；D0是频率因子；n是应力指数；b是伯格斯矢量；k是玻尔兹曼常数；G是剪切模量；T是热力学温度；Q是粘塑性变形的激活能；R是气体常数；-σ是等效应力。如果考虑键合过程中的加工硬化行为，等效应变速率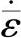
可以写为
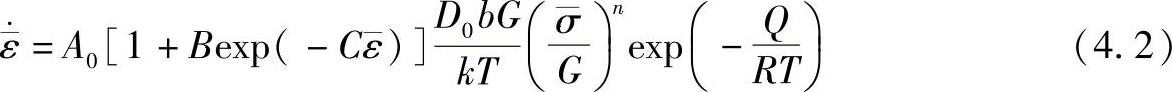
式中，B和C是无量纲常数；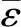
是由塑性变形引起的等效应变。当ε-足够大时，式（4.2）接近于式（4.1）。金和铝的材料常数如表4.1所示（Takahashi和Inoue，2002）(www.xing528.com)
表4.1 金和铝的材料常数
从式（4.1）和式（4.2）来看，必须考虑粘塑性变形的时间。Takahashi等（1993）建议用有限元方法模拟粘塑性键合过程。采用非线性、八节点带有拉格朗日乘子的等参单元分析大变形过程。有限元方法可以模拟两个不平整键合表面的接触过程，以及由于粘塑性变形引起的孔洞收缩。无论是忽略均匀或不均匀变形还是忽略体约束条件，两个键合表面的接触过程都受时间相关的粘塑性变形控制，其接触过程自然受边界条件的影响，如凸点的形状或者丝径或者焊盘的尺寸比。界面变形与接触面积的增加显著相关。理解随时间变化的塑性变形对于模拟微连接过程的界面变形非常重要。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
