基本因素与材料性能相关的热导率分析与应用案例

宏观焊接领域中采用的热和质量传递方程已经被外延到微观世界。然而，微观世界特征时间和距离比宏观领域中更短、更小。并且，当处理微零件中瞬间热流时，很可能发生近绝热条件，而当紧邻一个有效热沉时却是近稳态条件。当使用像激光或者电子束轻质高能量密度热源时，近绝热条件能导致极限传热率。热传递基本方程（傅里叶的抛物线热传导方程）和流体方程（纳维—斯托克斯方程）最终非收敛，而需要用考虑微小尺度下质能转换非连续性质的更复杂关系代替^[1]。

使用广泛采用的一维（1-D）热散失近似^[2]，局域化的热输入（如从激光脉冲中获得的）可依据下述方程进行热散失

x=（4αt）1/2 （3.1）

式中，x是距离；t是时间；α是材料的热扩散率。以钢为例（α为8mm²/s）^[3]，一个热脉冲需要大约3×10^-4s到达约100μm距离的一个边界，这比许多焊接激光的最短脉冲长度还要短。也许有人会质疑1-D近似对于许多实际几何结构来讲是一个很差的选择，但是这里的关键是临近边界（至少在微观尺度上临近）对热具有极大影响，可引起其或者近似混合参量解（若绝热），或者在短期内达到稳态（若等温）。对于微机电系统（MEMS）器件，其特征尺寸一般在几十微米左右，与不与基板（即大热沉）相连会造成迅速传热（绝热条件）和近定态条件的不同，其中，达到的最大温度是功率、材料导热率（对于MEMS器件，多晶硅是最好的热导材料）以及到最近热沉距离之间共同作用的结果。

一个1-D解析解（仅仅针对热传导）由卡斯劳和贾加尔（Carslaw and Jaeger）^[4]针对这样一个问题给出：“表面上具有固定通量的平板”，也就是接近加热要连接一个齿轮轴端部的情况（见第15章）。对于这种情况，边界条件可以这样描述：①初始温度为0的区域0<x<l，固定通量F₀在x=l处进入固体，在x=0处无热流；②类似地，除了在x=0处不是零通量条件外，温度也维持为零。第2种情况有必要进行讨论，其解为

式中，K是材料的热导率。由于解中包含了指数部分（ierfc函数）的总和，所以采用MatLab进行了数值估算^[5]。对于性能接近合金钢的材料，计算的温度分布随时间的关系进行绘制，如图3.1所示。(www.xing528.com)

对于长为5mm的轴，需要一段时间（几秒钟）来达到所使用的热通量令加热端熔化，所需的热通量为15×10⁶W/m²，接近一个由转换SEM形成的微电子束接头。该热通量只能使一个足够长的插针发生熔化，有利于减弱等温端热沉效应。明显地，端部熔化以前插针大部分被加热到很高温度。这是一把双刃剑，一方面，希望最小的总体热输入以避免对邻近热敏感部位的损伤；另一方面，对于像玻璃、Si等脆性材料，要避免尖锐的热梯度以防止断裂。如果插针缩短到100μm，达到必要的稳态所需时间降低到约为1ms，然而，由于热沉非常接近热源，最大温度（对于同一热通量）与新、旧轴长成比例地降低。因此，需要一个相当高的F₀值以使轴端部熔化，这不需要施加很长时间。集中热源应用的短时要求可由“SHADOW”激光焊接技术满足^[6]，在这项技术中激光束迅速地沿着接头扫过，这将在本节的其他章节详加讨论（见3.6.2节和第14章）。

相反地，如果待熔化的部位是有效绝热的，如“漂浮的”MEMS器件，需要相当少的热输入，因为仅有的热损失就是通过对流或者辐射造成的。尤其对于高热导率材料（如Si），一个简单的包含能量守恒的集中参数计算会给出零件温度对时间确定关系的合适结果。以一个数量级举例，将Si从室温加热到熔化状态需要7.2J/mm³（等于7.2nJ/μm³）^[7]。对于大约100μm×100μm×1μm的“绝热”MEMS器件，仅需要7.2mJ热能。对于Si，在相对较低的转换SEM电子束功率下施加大约10ms（750mW）。由于零件的温度会等温地有效升高，因此很难避免完全熔化，我们不妨采用可控的局部熔化连接工艺。

熔化形成焊接需要在热输入和热沉散热之间小心地寻求平衡，尤其是对于微小尺度并且没有有效热沉的零件更是如此。

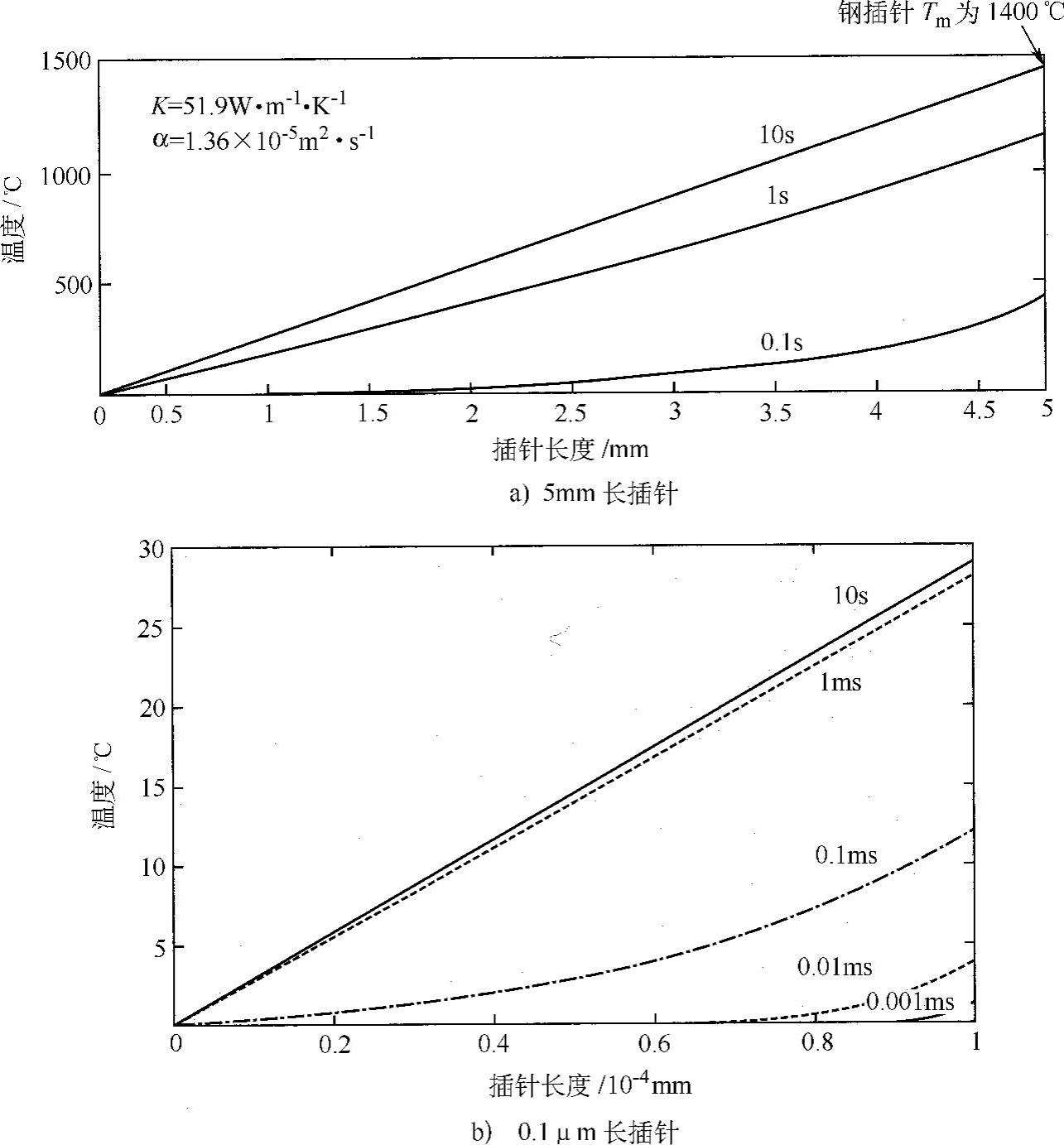
图3.1 等温端部条件热分布