热分解：探究1.7氧化物与污染物问题

如前面所述，键合线区域应变程度可以促进固相键合的产生。另外，前面所提及的模型中隐含了两个事实：接头区域仍然存在一定数量的污染；键合强度只能近似于母材。这两者间联系直接，如果焊缝中存在污染物，它们将减少焊缝的有效键合面积，并可能成为后续力学失效的萌生源^[21]。

工业应用中，为改进接头的键合性能，需进一步处理以减少焊缝中残留的污染物含量。对于许多金属体系来说，其氧化物一般都会随着环境温度的升高而逐步溶解到金属基体中。对于特定的氧化物M_xO_y来说，它在金属A中的溶解度可表示为

K_eq=Z（C_M）^x（C_O）^y （1.5）

式中，K_eq为平衡溶解度积；C_M和C_O分别为金属M和O在A金属中的含量；Z为关于活性系数的比例常数。如果氧化物本身为金属A的氧化物，那么公式可简化为

K_eq=Z（C_O）^y （1.6）

此时，Z为不同的比例常数。公式（1.6）表明，溶解度积是基体材料最大溶氧量的幂函数。对于基体材料的氧化物，利用合适的相图，可以获得氧在金属基体中的最大溶解度，从而估算溶解度积。此外，相图上氧的溶解曲线形状表明溶解度积与温度有关。公式（1.5）则表明与基体金属相关的非基体材料金属氧化物的溶解度积（同样具有温度相关性）也可根据相图进行预测。这里，溶解度积可以根据第二种金属和氧在基体金属中的最大溶解度进行预测。

若考虑氧在母材中的Raoultian行为，公式（1.5）和公式（1.6）中的比例常数等于1。根据氧的原子配比，选择合适的相图，就可以直接计算出不同种类金属的大致溶解度积。表1.2中列举了一些常见工程材料及其氧化物在母材中的大致溶解度积，这些溶解度积是在锻焊温度为0.9T_m下估算的。如表1.2所示，Al、Fe和Ti材料的氧化物在各自母材中的溶解度相差近30个数量级，Al的氧化物很难溶解到Al基体中，而Ti的氧化物却非常容易地溶解到Ti基体中。

表1.2 常见工程金属氧化物在各自母材中的大致溶解度 （考虑氧在母材中的Raoultian行为，锻焊温度为0.9T_m）

可以采用类似方法来计算非基体金属氧化物。Al₂O₃和Fe₂O₃在Fe中大致溶解度积的计算结果如表1.3所示。其中，两种氧化物的原子配比相同（x=2，y=3）。比较结果表明Al₂O₃在Fe中的溶解度相对较低。

表1.3 Al₂O₃和Fe₂O₃在Fe中大致溶解度积比较（锻焊温度为0.9T_m）

金属氧化物的溶解能力以及氧在基体中的扩散能力是扩散焊中氧化物溶解模型的基础^[22]，但大部分模型的假定条件均为：氧化物层是连续的；扩散溶解过程相对较长；都采用了氧化物层最大厚度来进行假设分析。这些模型都没有考虑表面应变作用后，氧化物层破碎后成为碎片和加热时间缩短的情况。(www.xing528.com)

针对这一问题，Ashby和Easterling^[23]提出了一个更好的模型来分析焊接过程中碳化物颗粒的溶解情况。这个模型考虑了离散颗粒（相对于连续氧化物层）的溶解。该方法既可以预测碳化物组元向基体中的溶解，又可以预测这些组元从分解的碳化物中扩散出去的能力。这种预测方法基于这样的假设：这些球状的颗粒可以完全从碳化物中分离出来并进入到一个半径为I的金属基体中，接着，这些颗粒将会按照一个轨迹溶解到金属基体中，该轨迹用时间和温度可定义为

式中，D∗和t∗为扩散系数（D为与温度T∗相关的函数）与时间（颗粒完全溶解到半径为I的金属基体中所需要的时间）的组合。

综合考虑扩散作用以及温度对颗粒溶解度积的影响，可对颗粒的溶解行为进行研究。以上关于氧化物溶解度积的讨论可用来描述氧化物颗粒的溶解情况，由此得出包括基体金属氧化物颗粒的控制方程为

对于非基体金属氧化物：

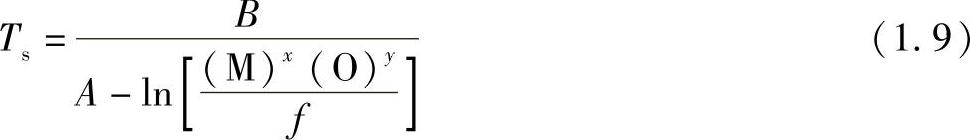
式中，T_s为溶解温度；A和B分别为对应溶解度积的温度系数；f为基体体积分数，f随着溶解过程中氧化物的不断减少而发生变化，f可定义为

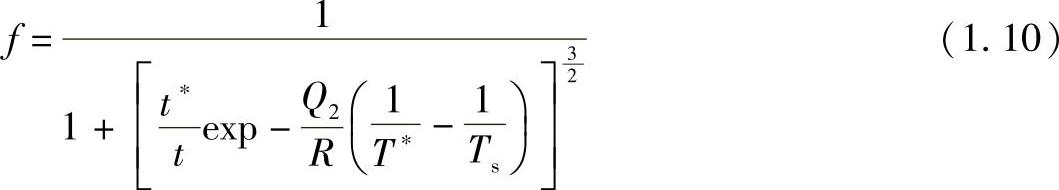
式中，Q₂为与扩散系数相关的激活能（氧或金属与氧）；R为理想气体常数。选择合适的t∗和T∗估计值，就可用公式（1.10）联合公式（1.8）或公式（1.9）建立起溶解过程中时间-温度曲线与氧化物溶解程度之间的直接联系。

在上述表达式中，t∗和T∗是直接描述氧化物颗粒尺寸以及位置分布的参数。它们具体值的选择可通过键合表面上氧化物的原始分布以及表面应变大致估算出来。

利用以上公式，可根据锻压程度以及时间-温度曲线对键合质量进行定性评估。随着接触面上应变的不断增大，氧化物颗粒尺寸和密度不断下降，随着氧元素的扩散，氧的数量相应减少，促进了氧化物的溶解。此外，焊接时间的加长也会促进氧化物的溶解。提高焊接温度不仅能促进扩散，而且提高溶解反应过程中的溶解度积。