直线旋转作图及注意事项

一、点绕垂直轴旋转时的投影

如图4-17（a）所示，点A绕正垂线O-O轴旋转时，O-O轴的正面投影为点o；水平投影o-o垂直于OX轴。点A的运动轨迹的正面投影是以o′为圆心，o′a′＝R为半径的圆；水平投影积聚为平行于OX轴长为2R的线段。当A点旋转θ角到达A1点时，其正面投影面转过θ角，由a′到a1′，其水平投影由a移到a1，如图4-17（b）所示。

如图4-18所示，点A绕铅垂线O-O轴旋转时投影作图的情形。运动轨迹圆的水平投影反映实形，正面投影积聚为平行于OX轴的长为2R的线段。

总之，点绕投影面垂直线作旋转时，其投影特性是：在轴线垂直的投影面上的投影作圆周运动，圆心为旋转轴在该投影面上的投影，半径是点在该面投影到圆心的距离（即点到旋转轴的距离）；在另一个投影面上，点的投影作与投影轴平行的直线运动。

图4-17 点绕正垂轴旋转

图4-18 点绕铅垂轴旋转

二、直线的旋转

直线的旋转可以归结为该直线上两点的旋转作图。在旋转过程中，两点必须遵守“三同”原则，即同轴、同向、同角。

图4-19所示为线段AB绕铅垂轴O-O顺时针旋转θ的作图情况。

为作图简便，可向o作oe⊥ab，然后oe顺时针转θ角后得oe1，再作a1b1⊥oe1，并取a1e1＝ae，e1b1＝eb，即得a1b1。

直线绕垂直轴旋转的特性为：在与旋转轴垂直的投影面上直线的投影长度不变，即直线对该投影图的倾角不变。

图4-19 线段绕铅垂轴旋转

1.将一般位置直线转为投影面平行线

如图4-20所示，将一般位置直线AB可以转为正平线。如AB为正平线，则正面投影反映实长，且与OX轴的夹角为α。旋转AB时，只有绕铅垂线旋转，才不改变AB对H面的倾角α，所以旋转轴为铅垂线。为作图方便，可使旋转轴通过点A，只需旋转点B就可以。具体作图步骤为：

（1）以a（o）为圆心，ab为半径画弧，使ab1∥OX轴。

（2）过b′作平行于OX轴的直线，在此直线上求出b1′。a′b1′＝AB，∠a′b1′b′＝α，如图4-20（b）所示。

图4-20 将一般位置直线旋转成投影面平行线

如图4-21所示，为直线AB绕正垂线轴旋转为水平线的投影图。图中水平投影a1b反映实长和对V面夹角β。

2.将一般位置直线转为投影面垂直线

一般位置直线要成为投影面垂直线，需要改变它对两个投影面倾角。因此，必须交替地绕垂直不同投影面的轴旋转两次，先将一般位置直线转成为投影面平行线，再将投影面的平行线转成投影面的垂直线。(www.xing528.com)

如图4-22（a）所示，一般位置直线AB第一次绕过点A的正垂线转成为水平线AB1（ab1，a′b1′）。如图4-22（b）所示，第二次水平线AB1绕过点B1的铅垂轴转成正垂线A2B1（a2b1，a2′b1′）。如果将AB转为铅垂线，需先绕铅垂线轴后绕正垂线轴旋转两次，如图4-23所示。

图4-21将一般位置直线旋转成投影面平行线

必须注意：连续旋转时，铅垂轴和正垂轴应交替使用，这与连续换面时应交替更换H面和V面的原理一致。

图4-22将一般位置直线旋转成投影面垂直线

图4-23 一般位置直线旋转成投影面垂直线

三、平面的旋转

平面由不在同一直线上的三点确定。因此，平面的旋转就归结为平面上点的旋转，这些点仍绕同轴、同向、同角旋转。平面的旋转有如下特性：

平面绕垂直于某个投影面轴旋转时，它在该投影面上投影形状不改变，平面对该投影面的倾角也始终不变。

1.将一般位置平面转为投影面的垂直面

与换面法类似，只需将一般位置平面上一条投影面平行线转为投影面的垂直线，则该平面也就成为投影面的垂直面。为了简便，在平面上选择一条投影面平行线，这样只需一次旋转，便可以达到目的。

如图4-24所示，是将一般位置平面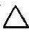ABC转为铅垂面，先做出平面内正平线AD（ad，a′d′），将AD绕过点A的正垂轮顺时针转成铅垂线AD1，然后分别旋转A、B、C三点，求出平面旋转后的正面投影a1′b1′c1′，再求出积聚的水平投影b1ac1和该平面对V面的倾角β6。

同理，也可将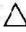ABC转为正垂面，并求出该平面对H面的倾角α，如图4-25所示。

图4-24 一般位置平面旋转成投影面垂直面

图4-25 一般位置平面旋转成投影面垂直面

2.一般位置平面转为投影面平行面

一般位置平面转为投影面平行面，需改变平面对两个投影面的倾角，因此，必须交替绕垂直两个投影面的轴连续旋转两次。第一次将平面变为一个投影面的垂直面，第二次将投影面的垂直面变为另一个投影面的平行面。

如图4-26所示，将一般位置平面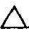ABC旋转为水平面。首先，作水平线AD（ad，a′d′），并将AD绕过点A的铅垂轴转为正垂线AD1（ad1，a′d1′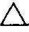），ABC随之转为正垂面AB1C1（ ab1c1，ab1′c1′）。其次，绕经过点B1的正垂轴，将AB1C1转为水平面A2B1C2（a2b1c2， a2′b1′c2′）。

图4-26 一般位置平面旋转成投影面平行面