换面法在V1/H体系中的应用及步骤

一、点的换面

1.使用换面法遵守的原则

（1）在新建的投影面体系中仍采用正投影法；

（2）新投影面必须对空间已知的几何要素处于最有利的解题位置；

（3）新投影面必须垂直于一个原有的投影面。

2.点的一次换面

（1）换V面，如图4-3（a）所示。A点在VH/投影体系中的投影为a、a′，现令H面不动，用新的铅垂面V1（V1⊥H）来代替V面，形成V1/H新投影体系和新投影轴为O1X1。过点A作投射线垂直于V1面，得到V11面上的新投影a1′，a1′和a是A点在新体系V1/H中的两个投影。然后将V1面绕O1X1轴旋转到与H面重合的位置，得投影图，如图4-3（b）、（c）所示。

图4-3 点的一次换面（换V面）

由于在V1/H体系中仍采用正投影法，所以a1′a⊥O1X1。另外，在V/H体系和V1/H体系中，具有公共的H面，所以点A到H面的距离（Z坐标）在两个投影体系中都是相等的， a1′a X1＝a′a X＝Aa，即更换V面，点的Z坐标不变。

（2）换H面，如图4-4（a）所示。用H1（H1⊥V）面代替H面，建立新投影体系V/H1，新投影轴O1X1，点A在H1面的投影为a1，如图4-4（b）、（c）所示。图中a′a1⊥O1X1，a1a X1＝aa X＝Aa′，即更换H面，点的Y坐标不变。

从以上更换V面和更换H面的投影图可以总结出点的换面规律：

1）新投影和被保留的旧投影的连线垂直于新投影轴；

2）新投影到新投影轴的距离等于被替换的旧投影到旧投影轴的距离。

图4-4 点的一次换面（换H面）

3.点的两次换面

在解题时，有时仅一次换面不能完成，需要进行二次或多次换面。

在更换两次或两次以上的投影面时，求点的新投影的作图方法和原理，与一次换面时完全相同，只是新投影面的设置要交替更换：

V/H→V1/H→V1/H2→V3/H2⋯⋯或V/H→V/H1→V2/H1→V2/H3⋯⋯

如图4-5（a）所示，为V/H→V1/H→V1/H2的变化情况，其作图步骤如下：

（1）先换V面，以V1面替换V面，建立V1/H体系，得新投影a1，此时a1′a X1＝a′a X。

（2）再换H面，以H2面替换H面，建立V1/H2体系，得到投影a2，此时a2a X2＝aa X1，如图4-5（b）所示。

二、直线的换面

1.一次换面

（1）把一般位置直线变换为投影面平行线。如图4-6（a）所示，AB在V/H投影体系中为一般位置直线，现选用平行于直线AB，且垂直于H面的平面V1为新投影面，组成新投影体系V1/H。在V1/H体系中，AB成为V1面的平行线，其新投影a1′b1′反映直线AB的实长，即a1′b1′AB，又因在变换过程中，直线AB与H面的相对位置始终未发生改变，所以a1′b1′与O1X1轴的夹角为直线AB与H面的倾角α。

图4-5 点的二次换面

在图4-6（b）中，为了使新投影面V1平行于直线AB，则新投影轴O1X1应平行于ab，新投影轴确定后，按照点的换面法，分别求出a1′，b1′，连接a1′b1′成为AB的新正面投影，且a1′b1′＝AB， a1′b1′与O1X1轴的夹角反映直线AB对H面的倾角a。

图4-6 一般位置直线变换为投影面的平行线

如图4-7是更换H面，求直线AB的实长和V面倾角β的作图过程。

图4-7 一般位置直线变换为投影面的平行线

（2）把投影面平行线变换为投影面的垂直线。如图4-8（a）中，在V/H体系中，AB为正平线，要使AB变换为新投影面的垂直线，所选的新投影面H1应垂直于正平线AB，因此它必垂直于投影面V。直线AB在新投影V/H1体系中为铅垂线，作图方法如图4-8（b）所示，其中O1X1⊥a′b′。

图4-8 投影面平行线变换为投影面的垂直线

如图4-9所示是更换V面，一次换面，将水平线变换为V1面的正垂线。

图4-9 投影面平行线变换为投影面的垂直线

2. 二次换面

若将一般位置直线变换为投影面的垂直线，必须变换两次投影面。第一次把一般位置直线变换为投影面平行线；第二次再把投影面平行线变换为投影面垂直线。

如图4-10所示为先变换V面，使直线AB在V1/H体系中成为正平线，然后再换H面，使直线AB在V1/H2体系中成为铅垂线。其作图方法如图4-10（b）所示，其中O1X1∥ab、O2X2⊥a1′b1′。

以上是先变换V面，后变换H面，两次换面，使一般位置直线AB成为铅垂线。(www.xing528.com)

同理，也可以经V/H H1/V→H1/V2变换，使一般位置直线成为正垂线。

图4-10 一般位置直线变换为投影面的垂直线

三、平面的换面

1.一次换面

（1）把一般位置平面变换为投影面垂直面。为使一般位置平面与新投影面垂直，只要使平面中的一条直线垂直于新投影面即可。如在平面中选择一条投影面的平行线，那么经过一次换面，就可以使这条平行线成为投影面的垂直线，包含此线的平面自然也成为投影面的垂直面。

在图4-11（a）中，ABC在VH/体系中为一般位置平面，CD是此平面中的水平线，更换V面为V1面，使V1面同时垂直于直线CD和H面。

图4-11 一般位置平面变换为投影面的垂直面

作图时，使新投影轴与ABC内水平线的水平投影垂直，即O1X1⊥cd。新轴确定后，利用点的换面法，可以求出ABC在V1面上的投影，此投影积聚为直线，可以反映出平面对H面的倾角α，如图4-11（b）所示。

同理，经过V/H→V/H1变换，求平面与V面倾角β,如图4-12所示，图中O1X1⊥b′e′（BE为面内正平线）。

（2）把投影面垂直面变换为投影面平行面。平行于投影面的垂直面设定新投影面，只需一次换面，就可以使之成为新投影面的平行面。图4-13（a）中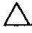，ABC为V/H体系中的正垂面，平行于该平面有积聚性的正面投影a′b′c′，设定O1X1轴，此时，在V/H1体系中，H1∥ABC，按点的换面法分别求出a1、b1、c　，连接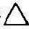a1b1c1就反映了ABC的实形。

图4-12 一般位置平面变换为投影面的垂直面

图4-13 投影面的垂直面变换为投影面的平行面

同理，如图4-13（b）所示，可经过V/H→V1/H变换，把铅垂面变换为正平面，且a1′b1′c1′反映ABC实形。

2.二次换面

若将一般位置平面变换为投影面的平行面，必须经过两次换面。综合前面两种情况，可以先经过一次换面，使平面成为新投影面的垂直面，第二次换面再使平面成为新投影面的平行面。

图4-14（a）所示，一般位置平面的ABC经过变换顺序V/H→V1/H→V1/H2，在H2面上得a2b2c2＝ABC。

图4-14（b）所示，变换顺序为V/H→V1/H1→V2/H1，在V2面上得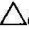a′2b′2c′2＝ABC。

图4-14 一般位置平面变换为投影面平行面

四、应用举例

用换面法解决空间几何问题时，应根据已知几何元素和待求几何元素之间的关系，分析它们与投影面之间处于怎样的相对位置，才能有利于解题，然后考虑如何换面，使之达到预想的位置。只有思路清晰、步骤合理，才能使作图简便。

例1 求点C到直线AB的距离，如图4-15（a）所示，并求出距离的投影。

分析：如图4-15（c）所示，将AB直线变为投影面的垂直线，则C点到AB的垂线CK必平行于该投影面，它的投影反映实长，此即为C点到AB的距离。

图4-15 求点C到直线AB的距离

解：作图步骤如下：

（1）先将AB 变为 V1面的平行线，作 O1X1∥ab， 得a1b1， 同时求出c1′。

（2） 再将AB 变为H2面的垂直线，作 O2X2⊥a1′b1′，得a2b2（积聚为一点）及 c2。

（3）作c1′k1′⊥a1b1′（c1′k1′∥O2X2），k2也积聚在a2b2处， 则c2k2即为c 点到AB 的距离。

（4）将点k从V1/H2体系返回到V/H体系，得CK的投影ck、c′k′，如图4-15（b）所示。

例2 过点K作ABC的垂线KL，如图4-16所示。

分析：KL⊥ABC，当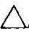ABC垂直某投影面时，KL应平行于该投影面。此时，它们的投影可以直接反映直角，容易解题。

图4-16 作一般位置平面的垂线

解：作图步骤为：

（1）作ABC内的水平线CE（ce，c′e′）。

（2）作新轴O1X1⊥ce，求ABC及点K 在V1/H体系中的投影a′1b′1c′1和k1′，a′1b′1c′1应积聚为直线。

（3）作k1′l1′⊥a′1b′1c′1，在H面上作kl∥O1X1轴。

（4）由l、l1′可求出l′，连接KL的各投影即可。