解决垂直问题：条件、投影和实例

一、直线和平面垂直

从初等几何定理可知，如图3-14所示，直线L⊥P面内相交直线AB、CD，则L⊥P面。

如图3-15（a）所示，直线ⅠⅡ⊥ABC，则必垂直于平面内的水平线BD和正平线AE，根据直角投影特性可得：12⊥bd，1′2′⊥a′e′，由此可得：若直线与平面垂直，则直线的水平投影垂直于平面内的水平线的水平投影，直线的正面投影垂直于平面内的正平线的正面投影；反之，若直线与平面的投影具备上述条件，则直线与平面垂直。

图3-14 直线垂直于平面的条件

图3-15直线垂直于平面的投影特性

例1 过点E作直线垂直于ABC，并求交点，见图3-16。

解：（1）在ABC中，过点A作水平线A1，并求其投影a′1′，a1；

图3-16 过点E作EF⊥ABC

（2）在ABC中，过点B作正平线B2，并求其投影b2，b′2′；

（3）过e′作e′f′⊥b′2′，过e作ef⊥a1，则EF即为所求；

（4）求交点——垂足k，并判别可见性。(www.xing528.com)

二、两平面垂直

如图3-17所示，直线L⊥平面P，且L∈平面Q，则平面Q⊥平面P，也就是说，如果一个平面经过另一个平面的垂线，则这两个平面相互垂直。

例：过点A作平面垂直于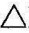ⅠⅡⅢⅡ。

解：（1）在1′2′3′中，作1′5′∥x轴，并求出15，作在123中作24∥x轴，并求出2′4′；

（2）过a′作a′c′⊥3′4′，过a作ac⊥15，则直线AC⊥ⅠⅡⅢ；

图3-17 两平面垂直的条件

（3）含点A作任意直线AB，则AB×AC所在平面⊥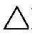ⅠⅡⅢ。

图3-18过点A作平面垂直于ⅠⅡⅢ

注：本题中，AC为唯一的，但过AC作ⅠⅡⅢ的垂直平面可有无穷多个解，上例仅是其中之一。