直线和平面相交,交点是直线和平面的共有点。两平面相交于一条直线,交线是两平面的共有线,直线与平面相交与两平面相交均可归纳为以下两种情况:
一、特殊情况
1.一般位置直线与特殊位置平面相交
由于特殊位置平面的某些投影有积聚性,因此,直线与特殊位置平面相交,可利用该平面投影的积聚性,直接求出交点的一个投影,然后再利用点的投影规律,或点的所属性原则,求交点的其他投影。
如图3-7所示,一般位置直线MN与正垂面ABC相交,ABC在V面的投影为直线a′b′c′,因为交点属于ABC,所以交点的V面投影一定在a′b′c′上。又因为交点又属于MN,所以交点的V面投影也一定在m′n′上,所以a′b′c′与m′n′的交点k′一定为MN与ABC交点K的正面投影,已知k′利用点的所属性原则,可求出K在H面的投影k。
为了增加图形的直观性,需要对直线与平面的重影部分判别它们的可见性,交点的投影为线段投影可见性的分界点,规定可见部分画粗实线,不可见部分画虚线。
判断可见性的一般方法是利用交叉直线的重影点。在图3-7上,判断MN在H面投影的可见性时,找出交叉直线MN与AB对H面的一对重影点1(2),Ⅰ∈MN上,Ⅱ∈AB上,分别求其V面投影1′,2′,ZⅠ>ZⅡ,所以k1可见,画实线,而另一段则不可见,画虚线。
例1 求直线AB与铅垂面 DEF的交点,见图3-8。
DEF的交点,见图3-8。
图3-7 判断可见性
图3-8 求直线与平面的交点
解:因为DEF为铅垂面,所以在H面上投影def有积聚性,直线AB与 DEF的交点K的水平投影k必为def与ab相交交点,根据直线上点的投影规律,由k求出k′。
DEF的交点K的水平投影k必为def与ab相交交点,根据直线上点的投影规律,由k求出k′。
因为DEF在H面投影积聚成线,遮不住直线AB,所以水平投影ab全部可见,但在V面投影中,重影点1′(2′),Ⅰ∈AB,Ⅱ∈DEF,Y1>YⅡ,所以k′1′可见,而交点另一侧则不可见,为虚线。
2.投影面垂直线与一般位置平面相交
投影面的垂直线与一般位置平面相交,其交点的一个投影重合在直线有积聚性的投影上,而另一个投影则可利用交点属于平面,用面上取点的方法求出。
例2 求正垂线EF与一般位置平面 ABC的交点,见图3-9。
ABC的交点,见图3-9。
解:因为EF⊥V面,所以e′(f′)积聚为一点,交点K的V面投影k′与e′(f′)重合。因为K∈ABC,所以k′∈a′b′c′,利用面内取点的辅助线法求出k。
选择EF与AC对H面的重影点,判别直线对面投影的可见性,如图3-8所示。
3.一般位置平面与特殊位置平面相交
两平面相交,其交线为一条直线。求两平面交线就是求两平面的共有线,也可求任意两个共有点的连线,也可求一个共有点,并确定交线方向。
如图3-10(a)、(b)为一般位置平面ABC与铅垂面EFGH相交,只要求出交线MN上的两个点M、N,连接即为所求,而M为AC与EFGH的交点,N为BC与EFGH的交点,平面与平面相交,转化为求直线与平面的交点的作图。
图3-9 特殊位置直线与一般位置直线相交
(1)求直线AC与EFGH的交点,在H面上求得ac与efgh的交点m,由m→m′;
(2)求直线BC与EFGH的交点,在H面上求得bc与efgh的交点n,由n→n′;
(3)连接nn,m′n′即为所求交线的投影;
(4)判别可见性,交线MN为两相交平面可见与不可见的分界线, ABC以MN为界, ABNM在EFGH之前,则ABNM在正投影上可见,即a′b′n′m′画粗实线。交线另一侧MNC在EFGH后,则二平面重合部分不可见,画虚线,其余画实线。又因为EFGH在ABC之后,所以e′h′与a′b′c′重合部分画虚线,两平面的水平投影均为可见。
ABC以MN为界, ABNM在EFGH之前,则ABNM在正投影上可见,即a′b′n′m′画粗实线。交线另一侧MNC在EFGH后,则二平面重合部分不可见,画虚线,其余画实线。又因为EFGH在ABC之后,所以e′h′与a′b′c′重合部分画虚线,两平面的水平投影均为可见。
图3-10 一般位置平面与投影面垂直面相交
图3-11 一般位置平面与投影面平行面相交
例2 求一般位置平面 DEF与水平面
DEF与水平面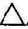 ABC的交线,见图3-11。(https://www.xing528.com)
ABC的交线,见图3-11。(https://www.xing528.com)
解:分析:求两平面交线,可求 DEF中任二条边与
DEF中任二条边与 ABC的交点,连接即可。
ABC的交点,连接即可。
作图:(1)求 DEF的边DF与
DEF的边DF与 ABC的交点。
ABC的交点。
因为 ABC为水平面,所以V面投影积聚成直线a′b′c′,找出a′b′c′与d′f′的交点m′,并求出m,如图3-11(b),即得交点M(m,m′)。
ABC为水平面,所以V面投影积聚成直线a′b′c′,找出a′b′c′与d′f′的交点m′,并求出m,如图3-11(b),即得交点M(m,m′)。
(2)求直线EF与 ABC的交点,同上,可求得a′b′c′与e′f的交点n′及n,得交点N(n,n′);
ABC的交点,同上,可求得a′b′c′与e′f的交点n′及n,得交点N(n,n′);
(3)连接nn,m′n′,可得交线MN的H面和V面投影;
(4)判断可见性,正投影均可见,因为MN为可见与不可见分界线,且MNF在ABC之上,所以mnf可见,反之,MDEN在ABC之下,所以水平投影重合部分不可见,见图3-11(b)。
二、一般情况
1.一般位置直线与一般位置平面相交
当直线和平面都处于一般位置时,交点的求法如下:
(1)过已知直线作辅助平面:为作图方便,辅助平面一般应作成特殊位置平面,可利用其积聚性;
(2)求辅助平面与已知平面的交线;
(3)交线与已知直线的交点即为所求。
图3-12作辅助平面P,求直线与平面的交点
例1 求直线DE与 ABC的交点,见图3-12。
ABC的交点,见图3-12。
解:(1)过DE作正垂面Pv。
(2)求两平面交线GH,Pv的正面投影积聚为g′f′,交AC于G,交BC于F,利用点的所属性可求得gf;
(3)de与fg交于k,且K点正投影k′在g′f′上和d′e′上,所以点K为直线DE与ABC的交点;
(4)判别可见性,方法与前面相同,结果如图3-12(b)所示。
2.一般位置平面与一般位置平面相交
例1 求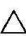 ABC和
ABC和 DEF的交线,见图3-13。
DEF的交线,见图3-13。
解:如图3-13(a)所示,两三角形的同面投影有相互重叠的部分,且DE与DF均与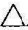 ABC直接相交,所以,可用求直线和平面交点的方法求出两个共有点,连接即为所求。
ABC直接相交,所以,可用求直线和平面交点的方法求出两个共有点,连接即为所求。
作图:
(1)含DE作平面Q⊥V面,求出DE和 ABC的交点K,画法见图3-13(a);
ABC的交点K,画法见图3-13(a);
(2)含DF作平面R⊥V面,求出DF和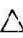 ABC的交点L,画法同上,见图3-13(b);
ABC的交点L,画法同上,见图3-13(b);
(3)连KL(kl,k′l′)即得所求交线;
(4)判别可见性,结果如图3-13(c)。
图3-13 利用线面交点法确定两平面图形的交线
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




