如何判断直线AB与三平行线？

一、直线与平面平行

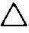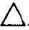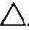根据初等几何所述：一直线与平面上任一直线平行，则直线与该平面平行，如图3-1（a）所示。直线AB∥直线CD，直线CD属于DEF，所以直线AB∥DEF，图3-1（b）表示了直线与平面平行的投影特征，由于ab∥cd，a′b′∥cd′，所以，直线AB∥直线CD，又因为直线CD属于DEF，所以直线AB∥DEF。

图3-1 判断直线与平面平行

例1 过已知点Ⅰ（1，1′），作平面与直线AB（ab，a′b′）平行，见图3-2。

解：分析：若过点作直线与AB直线平行，则含此直线所作的平面均平行于直线AB，所以过点Ⅰ，可作无穷个平面与直线AB平行。

例2 判断直线AB与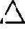ⅠⅡⅢ是否平行，见图3-3。

解：分析：在ⅠⅡⅢ中任取一点C，作CF∥AB，判断CF是否在平面ⅠⅡⅢ内，若在，则直线AB∥ⅠⅡⅢ，反之，则直线AB不平行于ⅠⅡⅢ。

（1）取1′2′上一点c′，作c′f′∥a′b′，cf∥ab。

（2）从图3-3中可以看出，f，在2′3′上，f在23上，且符合点的投影规律，所以CF属于ⅠⅡⅢ，故直线AB平行于ⅠⅡⅢ。

图3-2 含定点作平面与定直线平行

图3-3 判断平面与直线是否平行的作图

二、平面与平面平行

根据初等几何定理：若一平面内的相交两直线与另一个平面内的相交两直线平行，则此两平面平行。

图3-4 判断平面与平面平行

如图3-4（a）所示，平面P内相交两直线AB、BC，分别与平面Q内相交两直线DF、EF平行，即AB∥DE，BC∥EF，所以，平面P∥平面Q，图3-4（b）为其投影图。因为ab∥de，a′b′∥d′e′，所以AB∥DE，同理BC∥EF，又因为AB、BC交于B，且共属于平面P，DE与EF交于E，且共属于平面Q，所以P∥Q。(www.xing528.com)

例1 过点I作平面平行于ABC平面，如图3-5。

解：只要过点I作两相交直线，且分别平行于ABC的任两条边，则所作两相交直线所代表的平面即与ABC所在平面平行。

作1′e′∥b′c′1e∥ab

1′d′∥a′c′1d∥ac

则：平面、EID即为所求。

图3-5 过点I作平面与已知平面平行

例2 判断四边形ABCD与EFG 是否平行，见图3-6。

图3-6 判断两平面是否平行

解：分析：要判别两平面是否平行，只要看能否在一个平面上做出一对相交直线与另个平面上的一对相交直线平行，能做出，则平行，反之，则不平行。

作图：

（1）过a′作a′1′∥e′g′，a′2′∥e′f′；

（2）作出a1，a2，显然a1不平行eg，a2不平行ef。

所以，四边形ABCD与EFG不平行。