几何作图方法与符号应用介绍

机件的轮廓形状虽然是多种多样的，但其投影图形仍是由直线、圆弧及非圆曲线所组成的几何图形。为确保绘图质量，提高作图速度，除正确使用绘图工具和仪器外，还需要熟练掌握各种常见的几何作图方法。

一、任意等分已知线段

1.平行线法

现以四等分已知线段AB为例，如图1—36所示，说明如下：

图1—36 用平行线法等分线段

（a）过点A任意作一直线AC；

（b）用分规或直尺以任一适当长度在AC上截取或量取4等分点，得点1、2、3、4；

（c）连接B4，并分别过1、2、3点作直线平行于B4，且交AB于1′、2′、3′点，此三点便将AB四等分了。

2.试分法

现以图1—37所示的五等分已知线段AB为例，说明如下：

首先，估计选取约AB长度的1/5作为分规两钢针尖端的间距，并用分规对AB线段进行试分（至C点）。其次，使分规两钢针尖端间距增量1/5C′B长后，再重新试分。这样，经多次试分后，可实现将AB五等分。

图1—37 试分法等分线段

二、等分圆周和作正多边形

1. 二三等分圆周和作正三角形

已知圆心O和半径R，既可用圆规或分规来三等分圆周，如图1—38（a），也可用三角板配合丁字尺来三等分圆周，如图1—38（b）。顺次连接三个等分点，即可得正三角形，如图1—38（c）。

图1—38 三等分与正三角形

2.六等分圆周和作正六边形

（1）已知正六边形的对角线长（或圆的直径）时，作图方法如图1—39所示。其中，图1—39（a）图是用圆规或分规来等分圆周的：图1—39（b）图则是用三角板和丁字尺配合对圆周进行等分的。

图1—39 六等分与正六边形

图1—40 作正六边形

（2）已知正六边形的对边间距（S）时，可用三角板和丁尺配合来作图，如图1—40所示

3.五等分圆周和作正五边形

已知正五边形的外接圆时，其作图方法如图1—41所示，要领如下：

（1）二等分OA，得中点E，如图1—41（a）所示。

（2）在EC上取F点，使EF＝EB，如图1—41（b）所示。

（3）以BF为正五边形边长， 分圆周，顺次连接各点即可， 图1—41（c）所示。

图1—41 五等分与正1 五边形

三、斜度和锥度

1.斜度的概念与规定符号

斜度是指一直线（或平面）相对于另直线（或平面）的倾斜程度。其大小是以他们夹角的正切值来确定，并将此值简化为1∶n的形式，如图1—42（a）所示。

在图样上应采用图1—42（b）所示的图形符号表示斜度。按此图所示绘制其符号时，应以尺寸数字高度（h）的约1/10（h/10）作为线宽。

2.斜度的标注与画法

在图样上标注斜度时，需在1∶n前加上规定符号“∠”，即以“∠1∶n”的形式来表示。并要注意使符号的方向与斜度方向一致，如图1-43所示。

图1—42 斜度及其符号

图1—43 斜度的标注

斜度的画法，如图1—44所示。

图1—44 斜度的画法

3.锥度的概念与规定符号

锥度是指正圆锥的底圆直径与高度之比（对于正圆台，则为底圆和顶圆直径之差与其高度之比），并将此值化为1∶n的形式，如图1—45（a）所示。

图1—45 锥度及其符号

在图样上应采用图1—45（b）所示的图形符号（GB/T 15754—95）表示锥度，并按图中所画线宽和尺寸进行绘制。(www.xing528.com)

4.锥度的标注（GB/T 15754—95）与画法

在图样上标注锥度时，锥度符号应配置在基准线上，且应靠近圆锥轮廓标注。基准线应通过引出线与圆锥的轮廓线相连，且基准线应与圆锥的轴线平行。符号的方向应与圆锥方向一致，锥度值则应写在基准线上方，如图1—46所示。

锥度的画法，可按图1—46所示作出。从画图线的角度而言，也可先将锥度值转化为斜度值，然后按斜度画法作出；例如，先将该图中的锥度值由1∶6转化为1∶12，再根据斜度值为1∶12来按斜度画法作图。

图1—46 锥度画法与标注

当所标注的锥度是标准圆锥系列之一（尤其是莫氏锥度或米制锥度，见GB1443）时，可用标准系列号和相应的标记表示，如图1—47所示。

图1—47 锥度标注

四、圆弧连接

在实际机件上，常常会遇到一个表面通过某平面或曲面光滑地过渡到另一个表面的情形，这种过渡称为面面相切。其反映到投影图上，通常为一条线段通过某半径为R的圆弧与另一条线段光滑相连；这种情况的作图即称为圆弧连接，其中起光滑连接作用的圆弧称为连接圆弧。

1.圆弧连接的作图原理（见表1—13）

表1—13 圆弧连接的基本原理

圆弧连接的关键是准确地求出连接圆弧的圆心和切点（即连接点）的位置。其中，准确地求取圆心尤为重要，其作图原理是：

（1）若要使半径为R的连接圆弧与已知直线相切，则其圆心位置必须位于与已知直线相平行且间距为R的直线（即半径为R且与已知直线相切的圆弧的圆心轨迹线）上。

（2）与已知圆弧（半径为R1）相切的半径为R的圆弧，其圆心必然位于以已知圆弧的圆心为圆心，以∣R1±R∣为半径的圆弧上。其中，“＋”号为两者相外切时选用，“—”号为两者相内切时选用。

（3）与已知两线段同时相切的半径为R的连接圆弧，其圆心必然位于该连接圆弧分别与两已知线段相切时所作轨迹线的交点上。

2.圆弧连接的作图举例

常见的各种圆弧连接的作图方法和步骤见表1—14。

表1—14 各种圆弧连接的作图方法、步骤举例

五、工程上常用的平面曲线的画法

工程上常用的非圆平面曲线有椭圆、渐开线、摆线和螺线等，下面只介绍前两种平面曲线的作图方法。

（一）椭圆的画法

1.四心法

已知椭圆的长轴AB和短轴CD，用四心法近似画椭圆（如图1—48），其画图步骤如下：

（1）连接AC，以O为圆心，OA为半径，画弧交OC延长线于E；再以C为圆心，取CE为半径，画弧交AC于E1，如图1—48（a）所示。

（2）作AE1的中垂线，并使其交长轴于点3，交短轴于点1；再对称地取点4和点2；然后分别连接1与3、1与4、2与3、2与4并延长，如图1—48（b）所示。

图1—48 用四心法画椭圆

（3）分别以点1、2和3、4为圆心，1C长（即2D长）和3A长（即4B长）为半径画弧至与线13、14和23、24相交（M、N、M1、N1为交点）处，如图1—48（c）所示。

2.同心圆法

已知椭圆的长轴AB、短轴CD，其作图步骤如下，如图1—49所示。

（1）以O为圆心，分别以OA长和OC长为半径作同心圆；

（2）过O作12等分两同心圆周的直径线，得各圆周上的12个等分点；

（3）分别过大圆周上各等分点作短轴的平行线，同时分别过小圆周上各等分点作长轴的平行线。所得到的12个交点即为椭圆周上的点，顺次光滑连接，即为所求椭圆。

图1—49 同心圆法画椭圆

应当指出，所作的等分直径线愈多，即求出的交点（椭圆周上的点）愈多，所得椭圆的平面轮廓误差就愈小，即作图结果就愈精确。

（二）渐开线的画法

将绕在圆周上的一直线沿切线方向展开，如展开的过程是连续的纯滚动，则该直线上任一点的轨迹即为这个圆周的渐开线，如图1—50所示。其作图步骤如下：

图1—50 渐开线的画法

1.将圆周（也称基圆）分成若干等分（图中为12等分），并找出展开线上的对应等分点；

2.过圆周上各等分点向同一方向分别作圆的切线，并依次截取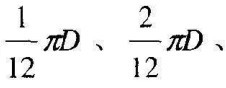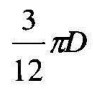⋯⋯πD；

3.顺次光滑连接各切线上的截取点，即得到了所求圆的渐开线。