IGBT等效电路模型解析

IGBT的等效电路模型是IGBT应用设计时进行Spice电路模拟的重要组成部分。IGBT等效电路模型的主要特点是通过调用已有Spice元件库中的相应元器件（BJT、功率MOSFET、电阻器等），置换相应的IGBT电参数，即可启动Spice直接模拟。不像其他的IGBT的Spice模型要提出专有的IGBT器件结构、用专有语言描述、需要专有的输入、输出格式等，并要嵌入到Spice程序中才能使用。相比之下，IGBT的等效电路模型思路简单、可靠性强，同时可满足绝大多数应用中对精度的要求。而IGBT的Spice模型虽然精度相对要高一些，但使用不方便。IGBT的等效电路模型的另一重要特点是它摒弃了过去IGBT模型建造中对瞬态分析准静态的条件假设，而是用更能体现IGBT工作状态的双极载流子输运理论对诸如轻掺杂外延层（N^-层）、大注入效应和低增益双极型晶体管特性等作了详尽的分析。

IGBT的等效电路模型可以准确地算出的IGBT的静态I-V特性、双极型晶体管增益及开关特性等。对IGBT的电导调制应用[压控电阻（Voltage Controlled Resistor，VCR）]进行等效，实测表明IGBT的等效电路模型的模拟结果与测量的结果对比符合较佳。

1.IGBT等效电路模型

优化的IGBT等效电路模型如图2-27所示，图中用VCR（压控电阻）等效IGBT的寄生PNP-BJT的宽基区（厚N^-区）的电导调制电阻。VCR用多变量函数表示的形式为

C_XXXN⁺N^-VCRPOLY（<ND>）<NC1⁺NC1^->

<NC2⁺NC2^->…P0<P1… （2-12）

式中，N⁺和N^-是VCR的两个电路节点；POLY（<ND>）表示该VCR函数的维数是ND；P₀＜P₁…是多变量函数的系数；NC1⁺和NC1-是控制该VCR的电压源在电路中的连接节点。

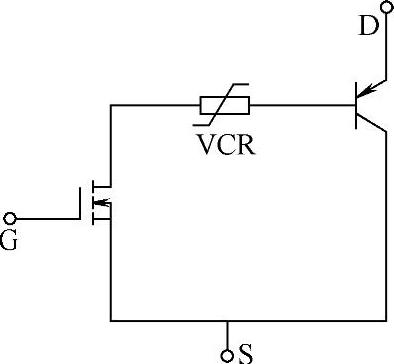
图2-27 IGBT的VCR等效电路模型

等效电路中的PNP-BJT和功率MOSFET可直接调用Spice标准库中的相应元器件。对BJT需要给出的基本模型参数为[area]（面积值）；I_S（饱和输运电流）；b_f（β_PNP放大倍数）；VCR，[Rb]（N^-层本征掺杂电阻）；[nf]（正向电流发射系数）等。而VD功率MOSFET的主要模型参数有W_ch（沟道总宽度），L_ch（沟道长度）；μ_ch（沟道迁移率），V_TH（阈值电压）；t_ox（栅氧厚度）；N_PB（P-阱掺杂）等。

以上参数可测量得到，如V_TH。其他参数可通过查器件手册或原始工艺文件得到，如t_ox，但大多数是用器件方程由测量数据推算出来的。2.功率MOSFET的阈值电压

功率MOSFET阈值电压V_TH为

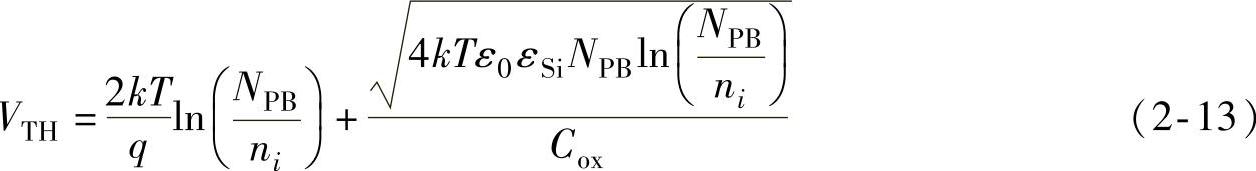
式中，q为电子电荷（1.602×10^-19 C）；k为玻耳兹曼常数（1.38×10^-23 J/k）；ε₀为真空介电常数（8.854×10^-12 F/m）；ε_Si为硅的相对介电常数（11.7）；T为绝对温度（T₀=300.15K）；n_i为本征载流子浓度（cm^-3）；为单位面积栅氧化层电容，其中ε_SiO2为栅氧化层（SiO₂）的相对介电常数（3.9）；t_ox为栅氧化层厚度（nm）。

由IGBT的饱和电流可计算出器件的沟道宽长比

式中，W_ch为沟道宽度（μm）；L_ch为沟道长度/μm；μ_ch为沟道电子迁移率（cm）；α_PNP为PNP-BJT的电流放大倍数；V_g为栅源极电压（V）；V_TH为阈值电压（V）；I_A为IGBT导通电流（A）。

功率MOSFET的沟道迁移率与温度的关系用下式表示：

μ_ch（T）=μ_ch（T₀）T_n^-2.5 （2-15）

式中，T_n=T/T₀。

3.宽基区PNP-BJT的参数(www.xing528.com)

双极晶体管的饱和电流I_S，是计算其I_B和I_C的重要参数，在大注入条件下，I_S可用下式计算：

式中，A为器件面积（cm²）（就是Spice参数[area]）；V_j为射基结（P⁺N^-）偏置电压（V）；m为大注入因子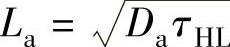；为双极扩散长度（μm），其中τ_HL为N^-区大注入过剩载流子寿命（μs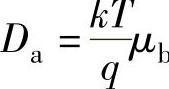）；为双极扩散系数（cm²/s），并用双极迁移率来表示：

该式就是所谓爱因斯坦关系。

轻掺杂N^-外延层，也就是宽基区电子和空穴迁移率与掺杂浓度及温度的关系，可按经验公式来计算：

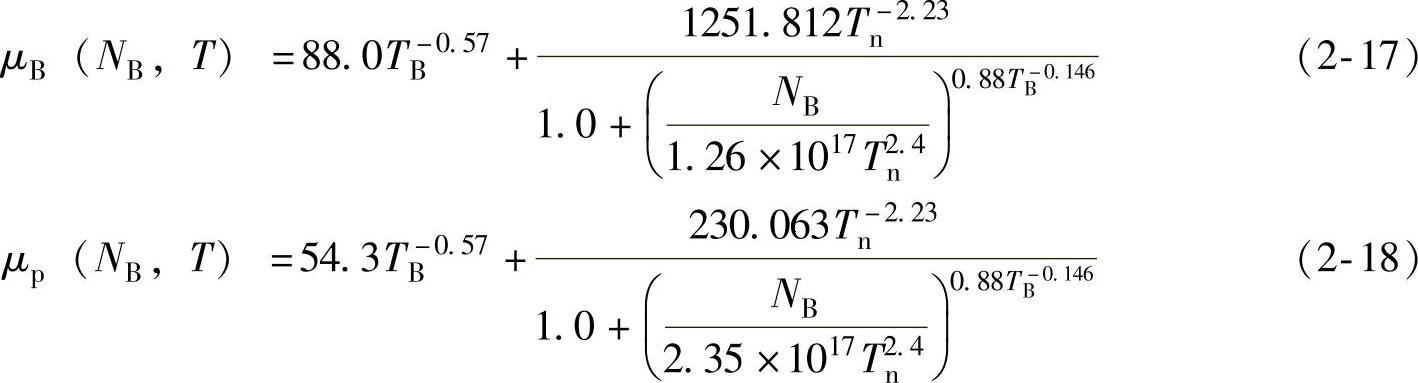
式中，N^-区掺杂浓度和厚度是由器件的击穿电压决定的。

准中性N^-区宽度（_μm）为

W=W_B-W_bcj （2-20）

式中，W_B=1.76×10^-6V_B^1.231，为冶金N^-区宽度（μm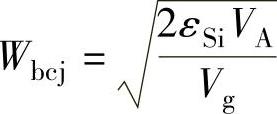）；为集电结（N^-/P阱结）耗尽区宽度（μm），V_A为IGBT的发射极和集电极电压（V）。

只考虑IGBT发射极和集电极电压，忽略其他控制电压的影响，N^-区的[VCR]电阻可表示为

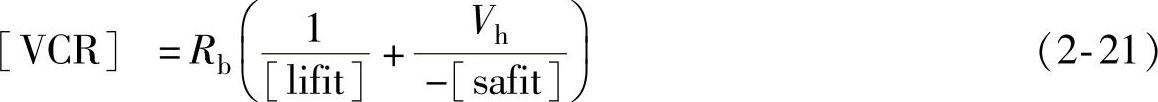
式中，R_b为轻掺杂N^-区的本征掺杂电阻，表示为；[lifit]和[safit]分别表示IGBT线性区及饱和区的复合（fit）因子

式中，α_PNP=γα_T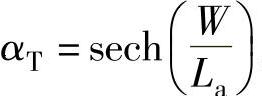，，是基区输运系数；γ是发射区（P⁺衬底）的注入效率，一般情况下，对于NPT型IGBT，γ取1。而对于PT型IGBT，γ受缓冲层厚度和掺杂的影响略有减小。

4.大注入载流子寿命（τ_HL）

半导体材料的寿命是复杂且影响因素较多的参数，并不存在计算寿命的系统和简单化的方法，多数情况下只能给出合理有效的估测，IGBT数据手册上开关速度的值可以作为τ_HL的初始值进行计算，再综合其他因素得到τ_HL的优化值，通常标准IGBT的开关速度为2～5μs，快速IGBT为1～2μs，超快速IGBT小于0.5μs，IGBT的开关速度主要与少子寿命有关。