设计模型优化：OptiStruct算例演示

本节通过OptiStruct完成若干算例的拓扑优化、形状优化和尺寸优化，每个例子通过问题描述、计算步骤和结果说明等演示OptiStruct是如何实现结构优化的。

图8-23 C形夹曲面模型

1）C形夹结构的拓扑优化

如图8-23所示为一个C形夹的曲面模型，优化目标是使用的材料最少，设计要求为：C形夹的开口部分，即图中的A和B处的节点在y方向的位移不能超过0.14 mm。

（1）优化问题建模。

优化目标：体积最小化。

约束条件：节点A在y轴方向的位移小于0.07 mm，节点B在y轴方向的位移大于-0.07 mm。

设计变量：单元密度。

（2）优化过程。

①在Hyper Mesh中载入几何数据或建立几何模型；

②定义材料属性和components；

③生成有限元网格；

④施加载荷和边界条件；

⑤创建载荷工况；

⑥使用Hyper Mesh设置优化问题：定义优化的设计空间；定义优化响应、约束和目标函数；⑦使用OptiStruct求解拓扑优化问题，确定最优的材料分布；

⑧对结果进行后处理。

（3）设计结果：密度分布结果如图8-24所示。

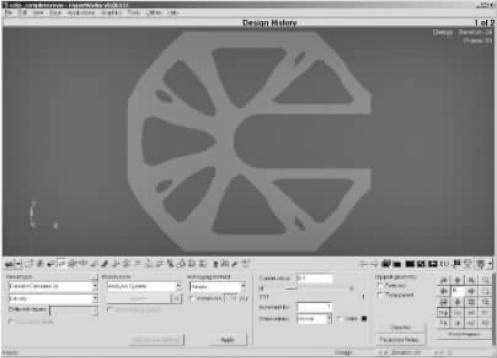
图8-24 C形夹拓扑优化设计结果

2）悬臂梁形状优化

如图8-25所示为一个悬臂梁模型，优化目标是体积最小，设计要求为载荷作用端最大位移小于3.0 mm。

图8-25 悬臂梁形状优化设计模型

（1）优化问题建模。

优化目标：体积最小化。

约束条件：梁的载荷作用端在向下的位移小于3.0 mm。设计变量：形状变量。

（2）优化过程。

①在Hyper Mesh中载入几何数据或建立几何模型；

②定义材料属性和components；

③生成有限元网格；

④施加载荷和边界条件；(www.xing528.com)

⑤创建载荷工况；

⑥使用Hyper Mesh设置形状优化问题：用Hyper Morph创建形状控制点；定义形状设计变量；定义优化响应、约束和目标函数；

⑦使用OptiStruct求解形状优化问题，确定最优解；

⑧对结果进行后处理。

（3）设计结果：如图8-26所示，节点1 115的位移达到约束值3.0 mm。

图8-26 悬臂梁形状优化设计结果

3）三维连接结构的尺寸优化

如图8-27所示为一个三维连接结构模型，该结构由壳单元构成。优化目标是体积最小，设计要求在给定的两个工况下，载荷作用点的位移小于许用值。给出的2个工况包括：图示载荷作用点x方向作用集中力F x=1.0×104 N，z方向作用集中力F z=1.0×104 N。

图8-27 3D连接结构尺寸优化设计模型

（1）优化问题建模。

优化目标：体积最小化。

约束条件：载荷作用端在给定工况下的x方向位移小于0.9 mm，z方向位移小于1.6 mm。

设计变量：壳单元厚度。

（2）优化过程。

①在Hyper Mesh中载入几何数据或建立几何模型；②定义材料属性和components；

③生成有限元网格；

④施加载荷和边界条件；

⑤创建载荷工况；

⑥创建尺寸优化设计变量；

⑦定义优化响应、约束和目标函数；

⑧使用OptiStruct求解尺寸优化问题，确定最优解；⑨对结果进行后处理。

（3）设计结果：如图8-28所示，长方体部分壳体厚度为0.99 mm，圆柱体部分壳体厚度为1.60 mm。

图8-28 3D连接结构尺寸优化设计结果

思考与练习

1.结构优化设计有哪些层次？分别适用于哪类问题？

2.结构拓扑优化方法有哪些？画出变密度法或ESO算法的流程图。

3.结构形状优化变量一般如何定义？

4.用相关结构分析和优化软件求下述问题最优拓扑优化结果：四边简支方板100 mm×100 mm×1 mm，中心承受集中力F=1 000 N，当体积分数为0.5时，使方板的刚度最大。