设计变量优化：形状改进策略

结构形状优化问题一般通过改变边界的几何形状来得到满足结构性能要求的最优设计，因此设计变量选取的好坏直接影响到优化结果的取舍。

结构形状优化设计中的设计变量是与结构的几何形状有关的。通常，形状设计变量确定了结构分析时的设计区域。例如，一个开槽的矩形块，如图8-16所示，槽的位置和尺寸由结构几何参数Cx、Cy、Dy、r1和r2确定，这5个参数就称为形状设计变量。不同的形状设计变量值会得到不同的结构形状，而不同的结构形状会产生不同的结构力学响应值。通常，这些形状设计变量在结构问题中并不是直接给出来的。

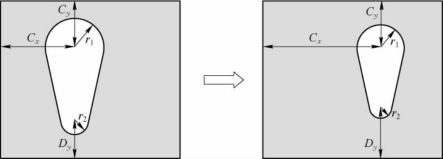
图8-16 形状设计变量

对于桁架结构的形状优化，一般选择节点坐标作为设计变量。对于连续体结构，形状优化的设计变量比较复杂，一般有以下方法。

（1）采用有限元网格的边界节点坐标作为设计变量，这种方法设计变量数十分庞大，同时优化过程中设计边界上光滑连续性条件无法保证，致使边界产生锯齿形状，或者有限元网格随着轮廓边界的移动出现扭曲或粗大，如图8-17所示，严重时会出现网格的畸变和退化，使形状优化失败。(www.xing528.com)

（2）采用边界形状参数化描写的方法，即采用直线、圆弧、样条曲线、二次参数曲线和二次曲面、柱面来描述边界，结构形状由顶点位置、圆心位置、半径、曲线及曲面插值点位置或几何参数决定，各类曲线或曲面的不同形式构成了各种不同的边界描述方法。这种方法解决了采用有限元网格的边界节点坐标为设计变量的缺点。

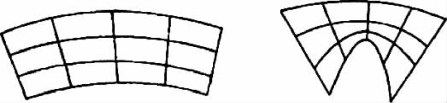
图8-17 有限元网格边界移动

（3）采用设计元方法，该方法把结构分成若干子域，每个子域对应一个设计元，设计元由一组控制设计元几何形状的主节点来描述，选择一组设计变量来控制主节点的移动。这种方法可以有效地减少设计变量，但是设计元在优化过程中也有网格致畸的缺点。

（4）用自然设计变量作为优化参数的形状优化方法，这种方法与前述三种以几何设计变量为优化参数的方法不同，它以加在结构控制点上的虚拟载荷为设计变量，认为虚拟载荷与相应产生的网格节点位移呈线性关系，并将该位移加到对应的节点坐标上构成新的有限元网格，然后由敏度分析确定新的虚拟载荷。如此反复，直至虚拟载荷为零。该方法的优点是优化过程中网格致畸的可能性较之几何设计变量方法有所降低。