现代的连续体结构拓扑优化是在1988年才开始的,Bendsøe和Kikuchi提出了具有开创性的均匀化方法,提出了连续体拓扑优化的概念和求解途径。目前,连续体结构拓扑优化方面的研究主要集中在:均匀化方法(homogenization method)、变密度法(variable materials method)、渐进结构优化方法(evolutionary structural optimization,ESO)和水平集方法(level set method)等。从结构拓扑优化方法的基本思路来看,可以将它们分为两类:①改变优化对象的材料特性,主要包括均匀化方法和变密度法,均匀化方法将结构变成多孔材料,而变密度法改变了结构的密度;②改变优化对象的几何形状,主要包括ESO方法和水平集方法。
1)均匀化方法
均匀化方法是连续体结构拓扑优化中最常用的方法,其基本思想是在拓扑结构的材料中引入微结构(单胞),微结构的形式和尺寸参数决定了宏观材料在此点的弹性性质和密度。优化过程中以微结构的单胞尺寸作为拓扑设计变量,以单胞尺寸的消长实现微结构的增删,并产生由中间尺寸单胞构成的复合材料,以拓展设计空间,实现结构拓扑优化模型与尺寸优化模型的统一和连续化。借助含有周期性分布微结构的复合材料,均匀化方法将拓扑优化设计问题转化为复合材料微结构参数的尺寸优化设计问题,应用优化准则法或数学规划方法来寻找多孔介质的最优分布。
基于有限元方法,在每个单元内构造不同尺寸的微结构,微结构的尺寸和方向为拓扑优化设计变量。如图8-11所示为一个微结构单元,该单元内布置a×b矩形孔的微结构,描述该微结构方位的角度为θ,而这三个变量a、b和θ即为微结构单元的设计变量。采用复合材料理论的均匀化方法,根据微结构的尺寸和方向能计算出每个单元材料的弹性矩阵,作为形成整体矩阵的依据。通过改变设计变量,优化实体和孔洞的分布,形成带孔的结构,实现结构拓扑优化设计。对于三维拓扑优化设计问题可以类似定义三维微结构,变量也会相应增加,处理方法与二维类似。

图8-11 均匀化方法的微结构
2)变密度法
变密度法1992年由Mlejnek提出,属材料(物理)描述方式的结构拓扑优化方法。变密度法的基本思想是人为引进了一种假想的密度可变的材料,其相对密度(人工密度)和杨氏模量之间的关系也是假定的,每个单元的人工相对密度为设计变量,将结构拓扑优化问题转化为材料最优分布设计问题,应用优化准则法或数学规划方法求解材料最优分布设计。变密度法中的人工密度是指材料密度和材料特性之间的一种对应关系。变密度法中的常见插值模型有:固体各向同性材料惩罚模型(Solid Isotropic Material with Penalization,SIMP)和材料属性的有理近似模型(Rational Approximation of Material Properties,RAMP)。SIMP或RAMP模型通过引入惩罚因子对中间密度值进行惩罚,使中间密度向0—1聚集,拓扑优化设计结果能很好地逼近实体和孔洞分明的0—1优化结果。惩罚因子的作用可解释为,通过惩罚使得设计变量在0到1之间的材料对结构性能(设计目标)的贡献降低,即使得这部分材料“不经济”,从而使得设计变量在优化过程中趋于0或1。SIMP和RAMP的材料密度—刚度插值模型如图8-12所示,通过引入惩罚因子p或q使设计变量的中间值对应的单元刚度逼近0,从而降低这部分材料对结构刚度的贡献。通过优化迭代,具有中间值的设计变量将趋于0或1。SIMP和RAMP的数学模型、结构刚度矩阵、应变能(柔顺度)及其对设计变量的偏导数可表述如下:
SIMP:Ep(xi)=E min+xj p(E0-E min)(8-5)
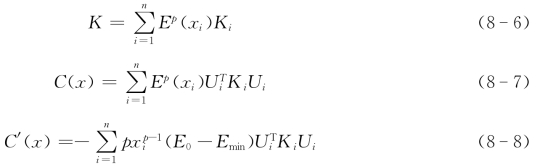
RAMP:Eq(xi)=E min+1+q
x
(1i
-x)(E 0-E min)(8-9)
i
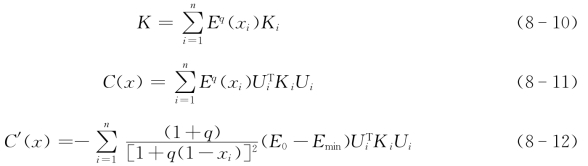 (https://www.xing528.com)
(https://www.xing528.com)
式中,n为单元数,xi是取值在[0,1]上的设计变量,为了避免刚度矩阵的奇异性,x min=0.001;p,q分别是SIMP和RAMP的惩罚因子;Ep(xi),Eq(xi)分别为SIMP和RAMP插值后的弹性模量;E 0,E min分别为实和空的单元的弹性模量,为了避免刚度矩阵的奇异性,E min取千分之一倍的E 0;Ki,K分别为单元的单位刚度矩阵和结构的整体刚度矩阵;U,C,C′分别为结构的位移向量、柔度和柔度对设计变量的灵敏度。
变密度法虽然具有程序实现简单,计算效率高,应用相对简单等优点,但是由于材料的伪密度和刚度的关系是人为假定的,其对结果的影响仍需进一步研究。

图8-12 材料的密度—刚度插值模型
3)渐进结构优化方法
渐进结构优化方法是1993年由澳大利亚华裔学者谢亿民和Steven提出,主要用于连续体结构拓扑优化设计问题。通过逐渐将无效或低效的材料删除,实现连续体结构拓扑优化,避免了多变量数学规划求解。ESO法的思想源自于力学准则法,代表了一类基于力学准则法的拓扑优化设计方法。一般过程是反复进行有限元分析,按计算结果根据给定的材料演化策略,在低应力区删除一定比例的材料,或在高应力区添加一定比例的材料,逐渐逼近等应力结构,直至得到最优解。
下面以应力优化为例,简单介绍渐进结构优化法的原理和实施步骤。由于结构中的应力分布一般并不均匀,应力较高的区域是结构发生破坏的主要部分,需要添加材料;而应力较低的区域,材料没有得到充分的利用,可以去除这部分材料,达到同时节省材料和减重的目的,且对整个结构的性能影响很小。因此,渐进结构优化的应力优化准则为:逐渐去除结构中的低应力材料,使剩下的结构更有效地承担荷载,从而应力分布更加均匀。具体实施步骤如下:
第一步,在给定的荷载和边界条件下,定义设计区域,称为初始设计,用有限元网格离散该区域;
第二步:对离散的结构进行静力分析得到设计区域的应力分布;
第三步:明确强度理论,例如,对平面应力状态下的各向同性材料,可采用Von Mises应力准则,求出各单元应力σeVM和最大的单元应力σV mMax,如果σeVM 满足
![]()
则认为该单元处于低应力状态,可从结构中删除,其中RRi为删除率;
第四步:重复第二步的有限元分析和第三步的删除单元,直到(8- 13)式无法满足为止,即对应于RRi的稳定状态已经达到,为使迭代继续进行,引入另一参数进化率ER,从而下一稳定状态的删除率修改为
根据数值经验,迭代过程中初始删除率RR0和进化率ER通常取1%;
第五步:重复第二~四步直到结构质量或最大应力达到给定值。
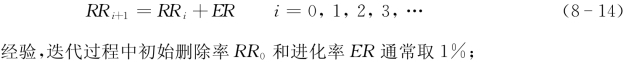
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




