如何求解结构优化问题？

求解结构优化问题有各种方法，其中最主要的是数学规划法（mathematical programming，MP）和优化准则法（optimality criteria，OC）。下面由简单到复杂，列出相关的求解优化问题的途径。

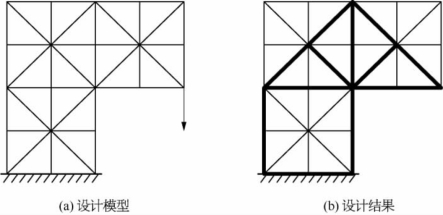
图8-6 桁架结构尺寸优化设计例

1）枚举法

为了求得最优解，最自然的想法是对所有可能的设计进行逐个检查，判断是否可行，若可行，则进一步比较它们的目标值，从中选取最优的，这就是枚举法。

2）网格法

由于一般设计变量在一定范围内可以任意取值，因此即使对最简单的问题，也无法穷尽所有可能的设计。作为枚举法的一个近似处理方法，可使设计变量从初值开始，以一定的步长增长，直到最大值为止。对每一个取值，判断其是否可行，并对可行解比较目标值，最终确定最优解，这种方法即为网格法。网格法的优点是简单，但仅适用于最简单的问题，因为随着设计变量的增加及步长的缩短，计算量急剧增长，且步长不能过大，否则有可能丢失最优解。

3）图解法

图解法是在设计空间中画出可行域和目标函数的等值面，再在图形上找出既在可行域内（或其边界上），又使目标值最小的设计点的位置。对式（8-2）所示的设计问题，可画出图8-7所示的可行域和目标函数等值线，最终可得到与约束h1与h2的交点为最优设计点X*（2，4），此时目标函数值为-18。一般情况下，最优点可能出现在约束曲面与目标函数等值面的切点上，也可能出现在可行域内部。显然，图解法很直观，但由图解法得到的解较粗糙，且难以适用于设计变量多于三个的问题。

图8-7 可行域与最优解

除了上述各种方法，对于简单问题有时还可采用解析法求出闭合形式的解。但是对于大多数工程实际的结构优化问题，以上方法都很难实施，一般需采用数值方法迭代求解，从20世纪60年代初期开始，在结构优化领域，这类基于迭代的数值优化方法基本上沿着两个方向发展，即数学规划法和准则设计法。

4）数学规划法

数学规划法是20世纪50年代前后蓬勃发展起来的一个数学分支，研究形如式（8-1）的非线性规划问题的求解方法和理论。根据设计变量、约束条件和目标函数的不同特点，存在许多不同的求解方法，形成了数学规划法中的不同分支。一般可描述为：从一个初始设计x（i）出发，对结构进行分析，利用分析得到的信息，按照某种方法决定一个可以使目标函数减少且满足某种要求的探索方向d（i），然后再决定沿这个方向应当前进的探索步长α（i），得到一个改进设计。迭代公式为：(www.xing528.com)

对于得到的新设计x（i+1），检查某种收敛准则，如果不满足，则以x（i+1）为出发点重新进行分析和设计。决定探索方向d（i）和步长α（i）的方法有多种，可根据问题的特点选择，如单纯形法、最速下降法、牛顿法等。

基于迭代的数值优化方法的一般步骤如图8-8所示，每一步迭代通常由两部分组成：①结构分析与收敛性检验；②修改模型参数获得一组新的设计变量值。由于做一次结构分析花费时间很多，所以需尽可能减少结构重分析的次数，在此前提下，可进一步减少优化处理（重设计）的工作量。

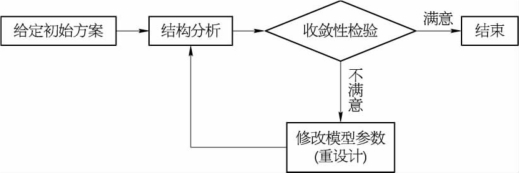
图8-8 数值解法流程

5）准则设计法

准则设计法是从满应力准则设计方法发展起来的，广泛应用于工程实际问题中。满应力准则是一种简易可行的结构优化方法，它遵循的设计思想是：结构的每一个构件至少在一种荷载工况下应力达到饱满，构件的材料被得到充分地利用，由它们组成的结构重量应该最轻的。

在20世纪60年代，满应力准则被推广用来考虑其他约束条件，例如位移及稳定临界荷载、频率等约束，这些准则通常设定为，按一定方式定义的某种虚应变能在结构内各点取常数。用准则设计法求解结构优化问题时，通常从一个初始设计x（i）出发，按照以下迭代公式进行迭代寻优：得到改进的新设计x（i+1）。依据采用的准则来构造迭代公式（8-4），因此所谓改进的设计也就是满足准则更好的设计。如果新设计x（i+1）以足够的精度满足提出的准则，那么迭代结束时，x（i+1）便是要求的最优设计，否则再重复以上的计算过程。

该方法是从工程观点出发，提出结构达到优化设计时应满足的某些准则，如满应力准则、能量准则等，然后用迭代法求出满足这些准则的解。这些优化准则大多数是根据已有的实践经验，通过一定的理论分析、研究和判断得到的，所以它是一种工程方法，它所得到的设计通常只是接近最优。

6）数学规划法与准则设计法的结合

作为结构优化设计方法的两大分支，数学规划法和准则法各有长短。准则设计法是从力学原理出发，建立一些最优准则，从而寻求用解析形式表达的结构设计参数，或者通过直观的迭代运算决定结构各单元的截面参数，但是缺乏严格的数学基础。准则设计法的主要特点是收敛快，重复分析次数少，且与设计变量数目无直接关系，计算工作量不大，但依赖具体的问题。数学规划法是从解极值问题的数学原理出发，运用数学规划中的各种方法，求得一系列设计参数的最优解，但是其计算效率并不理想。随着设计变量的增加，要求的迭代次数急剧增加，计算工作量增加得很快，这就使得在相当长的时间内，数学规划法的使用只限于较简单的问题。随着计算机能力的提高和数学规划法研究的进展，数学规划法求解规模也在不断增大。数学规划法的主要特点是，通用性好，有比较严格的理论基础，不依赖具体问题，但计算量大。

在20世纪80年代前后，结构优化数值方法的研究取得了多项重要的进展，其中之一是数学规划法和准则设计法的统一。作为准则设计法，人们发现可以利用数学规划中的最优化准则严格地推导出设计准则，而为了解决准则设计法遇到的有效和无效约束区分、主动和被动变量区分的困难，可以采用数学规划法中许多已经成熟的方法。另一方面，作为数学规划法，为了提高它的求解效率，人们发现需要充分利用结构优化问题的特点，利用传统的准则设计法中引进的各种近似。因此，结合这两种方法的混合法相继出现，如混合法、序列二次规划法（sequential quadratic programming，SQP）、移动渐近线方法（method of moving asymptotic，MMA）等。与数学规划法迅速发展相应，准则设计法也继续在一些涉及非线性动力响应等的优化问题中得到应用。

7）其他方法

随着计算机软硬件技术和计算科学的进步，还出现了一类启发式方法。例如，模拟生物进化的遗传算法，模拟金属凝固过程的模拟退火算法，模拟蚂蚁群体觅食的蚁群算法，模拟乐队演奏的和谐算法等。这类算法的适应性广泛，可以将商用的结构分析软件作为黑箱使用，因此降低了编程工作量，但计算工作量非常大。