结构优化设计问题分类

结构优化设计主要依赖于目标函数、约束条件和设计变量的类型，不同的设计变量需要用不同的数学方法来处理。结构优化按照设计变量的类型和求解问题的难易程度，可分为尺寸优化（尺寸变量）、形状优化（形状变量）和拓扑优化（拓扑变量）三个层次，分别对应于三个不同的产品设计阶段，即详细设计、基本设计及概念设计三个阶段，结构优化设计的三个层次和对应的产品设计阶段如图8-2所示。根据问题的复杂程度，通常认为拓扑优化设计比形状优化设计和尺寸优化设计更具难度。

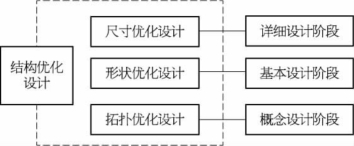
图8-2 结构优化的三个层次及对应的产品设计阶段

1）拓扑优化（topology optimization）

拓扑优化是指通过寻求结构的最优拓扑布局，包括连续体结构内有无孔洞，孔洞的数量、位置，桁架结构内杆件的有无以及相互连接方式等，使得结构能够在满足一切有关平衡、应力、位移等约束条件的情形下，将外荷载传递到支座，同时使得结构的某种性能指标达到最优。拓扑优化是一种比尺寸优化、形状优化更高层次的优化方法，也是结构优化中最为复杂的一类问题。拓扑优化处于结构的概念设计阶段，其优化结果是一切后续设计的基础。当结构的初始拓扑不是最优拓扑时，尺寸和形状优化可能导致次优结构的产生，因此在初始概念设计阶段需要确定结构的最佳拓扑形式。在新结构（或产品）开发过程中，若无设计资料可借鉴，则拓扑优化将起到非常重要的作用，因此拓扑优化设计对理论界有很强的挑战性，对工程界也有很大的吸引力。

对于离散的杆系结构，如桁架或框（刚）架结构，拓扑优化确定结构最佳的传力路线，或者是最少的构件数量及正确的连接形式，确定节点以及节点之间的杆件在空间的排列顺序，如图8-3a所示的设计模型，通过结构拓扑优化设计，可得到图8-3b所示的最优桁架结构。对于连续体，拓扑优化要在给定的设计区域内，对一定量（质量或体积）的材料进行合理配置和分布，使结构在给定载荷下，满足结构某项性能最优的设计准则要求，通常这种设计准则是“最大刚度”或“最大频率”等。图8-4为一个连续体结构拓扑优化设计例，图8-4a所示是初始设计模型，四角简支的壳体承受中心集中载荷作用；图8-4b所示是设计结果，其中黑色表示有材料，白色表示没有材料，可见拓扑优化的结果给出了最佳的材料分布形态。拓扑优化设计由于设计自由度大，比形状优化和尺寸优化的设计效益高，更能节省材料，其基本的理念可理解为：将低效的构件或材料从设计区域内删除，使结构以最佳的布局方式传递外力。

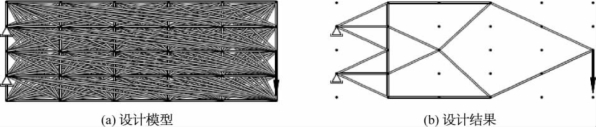
图8-3 桁架结构拓扑优化设计例(www.xing528.com)

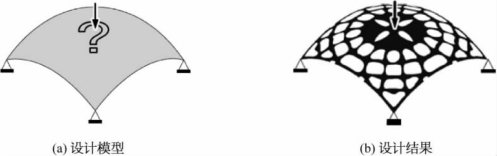
图8-4 连续体结构拓扑优化设计例

2）形状优化（shape optimization）

结构形状优化设计是通过更新设计域的形状和边界，寻求结构最理想的边界和几何形状，同时获得最优的性能指标。在连续体结构中，可确定结构内部或外部的几何边界形状，或两种材料之间的界面形状；在桁架或刚架结构中，可通过控制节点的位置来确定形状。形状优化属于可动边界问题，其目的是为了改善结构内力传递路径，以达到结构最优的力学性能。图8-5a、b分别为桁架结构和连续体结构形状优化设计的例子，图8-5a的上图是初始设计，下图是最优形状；图8-5b为优化设计后，结构中心的圆孔变成了椭圆孔。由图所知，形状优化不改变结构原来的拓扑构型设计，既不增加新的空洞或节点，也不允许有孔洞或节点重合而引起单元删除现象。

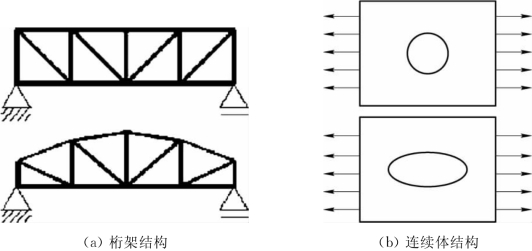
图8-5 结构形状优化设计例

3）尺寸优化（size optimization）

在优化设计过程中，以结构的尺寸参数作为设计变量，如桁架的杆件横截面尺寸、板的厚度和复合材料的分层厚度或铺层角度等，在满足结构的力学控制方程、边界条件以及诸多性态约束条件的前提下，寻求一组最优的结构尺寸参数，使得关于结构性能的某种指标函数达到最优。与拓扑优化或形状优化相比，尺寸优化比较简单。因为在优化过程中，不需要有限元网格重新划分，而且设计变量与刚度矩阵一般是线性或简单的非线性关系。图8-6为一个桁架结构尺寸优化的例子，通过寻求一组最优的桁架中各杆的截面积，在满足受载点位移约束的前提下，使桁架的重量最小。图8-6a为初始设计模型，图8-6b是最终的设计结果，图中加黑的线条表示应有的杆件，线条的粗细表示杆件的截面积大小。