理想气体的热力学转化过程

工程热力学中把实际热力设备中的各种过程近似地概括为几种典型的过程，即定容、定压、定温、绝热等过程。同时，为了简化，不考虑实际过程中的能量损失而将之作为可逆过程对待，工质看作理想气体。这种简化使得我们可以用较简单的热力学方法给予分析计算。

为了突出研究过程中热能与机械能转换这一核心问题，我们重点讨论闭口系统。

（一）定容过程

定容过程即气体在状态变化过程中体积不变的过程，即比体积保持不变。

过程方程为

v=常数 （2-23）

过程中状态参数之间的关系，根据理想气体的状态方程，有

p/T=常数 （2-24）

即 p₂/p₁=T₂/T₁ （2-25）

式（2-25）即说明定容过程中气体的压力与绝对温度成正比。

此过程中，加给气体的热量全部转变为气体的内能，即

q=Δu=u₂-u₁ （2-26）

引用比定容热容，定容过程中的热量还可以表示为

q=c_V（t₂-t₁）=c_V（T₂-T₁）=u₂-u₁ （2-27）

工质的内能只是状态的函数，而与过程无关。因此，两个状态之间工质内能之差也只取决于这两个状态，而与这两个状态之间连接一个什么样的过程无关。所以，上边得到的式（2-27）尽管是由定容过程得出的，但它对于定比热容理想气体具有普遍意义。

（二）定压过程

定压过程是工质在状态变化过程中压力保持不变的过程，其过程方程为

p=常数 （2-28）

过程中状态参数间的关系为

v/T=常数 （2-29）

即v₂/v₁=T₂/T₁ （2-30）

定压过程中工质的比体积与绝对温度成正比。

根据热力学第一定律，可得定压过程中的热量为

q=u₂-u₁+p（v₂-v₁）=h₂-h₁ （2-31）

即定压过程中工质吸收的热量等于其焓增，或放出的热量等于其焓降。

引用比定压热容c_p，则定压过程的热量为

q=c_p（t₂-t₁）=c_p（T₂-T₁）=h₂-h₁ （2-32）

既然焓只是状态的函数，那么，在求定比热容理想气体的焓差时，虽然式（2-32）是由定压过程得出的，但它对于定比热容理想气体具有普遍意义。对于任何过程，定比热容理想气体的焓差均可由下式求得，即

Δh=h₂-h₁=c_p（t₂-t₁） （2-33）

由q=u₂-u₁+p（v₂-v₁）=c_V（t₂-t₁）+R（T₂-T₁）=（c_V+R）（T₂-T₁）可知

c_p=c_V+R （2-34）

比定压热容与比定容热容之比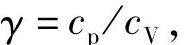结合式（2-34）可得

（三）定温过程

工质在状态变化过程中温度不变的过程叫做定温过程，它的过程方程为

将该关系结合状态方程pV=RT，可得理想气体定温过程中状态参数间的变化关系为

即理想气体温度不变时，压力和比体积互成反比。(www.xing528.com)

（四）绝热过程

绝热过程是状态变化过程中任何一段微元过程中工质与外界都不发生热量交换，并且工质内部相互之间不发生热量传递的过程。因此，在过程进行的任何一个微元过程中，恒有

整个过程中工质与外界交换的热量当然也为零，即

对于理想气体的可逆绝热过程，可以推得

这就是理想绝热过程的方程式。γ就是比热容比。由于γ是绝热过程方程式的指数，故又称其为绝热指数。

绝热过程初、终态参数的关系可由状态方程及绝热过程方程式求得。

因为

从而

考虑到状态方程可得

和

应用上述三个关系式，就可以根据相应的已知条件确定其他参数。

下面简单讨论一下开口系统绝热过程中的功。

根据稳定流动能量方程，在绝热过程中，工质对机器所能做的功为

如果忽略流速项，则有

这表明，工质在绝热过程中所做的功等于焓降。式（2-45）对理想过程和实际过程都是适用的。对于定比热容理想气体，有

（五）多变过程

前面讨论的是几种特殊过程，状态变化过程中某一个状态参数保持不变，或者在过程中与外界没有热量交换。实际热机中有些过程所有参数都有明显变化，而且与外界交换的热量也不算小，因而难以忽略。这类过程理论上难以分析，但其过程特性可通过实验确定。实验表明，许多过程的p-v关系比较接近指数方程式，如取1kg工质来研究，过程方程式为

热力学中将符合上式的状态变化过程称为多变过程，n叫做多变指数。

（六）过程综述

将上面讨论的定温、定压、定容、绝热四个基本过程画在同一个压容图上。如图2-6所示。这四种基本过程都可看作是多变过程的特例。

对定温过程，pv=常数，即n=1，所以多变指数n=1的多变过程即为定温过程。

对定压过程，p=常数，即n=0。

对绝热过程，pv^γ=常数，即n=γ。

对定容过程，v=常数。多变过程方程可以写作p^1/nv=常数。故定容过程中p的指数为0，这相当于n→∞的情况。

因此可以说，定容过程的多变指数n→∞。

图2-6 基本热力过程

由图2-6所示可以看出，多变指数n在坐标图上的分布是有规律的。由n=0开始沿顺时针方向，n逐渐增大，由n→1→γ→∞。因此对于任何一个多变过程，只要知道其多变指数，就能确定过程线在p-v图上的位置。