热力学第一定律：能量守恒在热现象中的应用

热力学第一定律是普遍的能量守恒与转化定律在热现象上的应用。它指出：自然界中的一切物质都具有能量，能量不可能被创造，也不可能被消灭；但能量可以从一种形态转变为另一种形态；在能量的转化过程中，一定量的一种形态的能量总是确定地相应于一定量的另一种形态的能量，能的总量保持不变。

（一）内能

能量是物质运动的量度，运动有各种不同的形态，相应地就有各种不同的能量。在宏观上静止的物体内，其内部的分子、原子等微粒仍处在不同的运动之中，这种运动叫热运动，物体因热运动而具有的能量叫做内能，又称热力学能。

内能是存储于物质内部的能量，内能的量值取决于物体内部微观热运动的状态。对于气体，它的内能包括：

1）分子的移动动能；

2）分子的转动动能；

3）分子内部和振动动能；

4）分子间由于具有相互作用力而产生的分子间的位能——分子的内位能。

对于理想气体，其内能只与温度有关。对于实际气体，其内能取决于气体的温度和比体积。由于温度和比体积是工质的基本状态参数，因此，内能是工质状态的函数。

内能的符号是U，1kg工质的内能用u表示。

工质的内能是无法直接测定的，也没有必要去确定内能的绝对数值。工程中感兴趣的是工质从一种状态变化到另一种状态时内能的变化，即两种状态下内能的差值。因此，可以人为地规定一个内能的零点。对于理想气体，通常规定热力学温度零度（0K）时工质的内能为零，有时也以0℃时的内能值为零。规定了内能零点后，可以根据计算或实验求出各不同温度下气体的内能，做成表格供查用。查表时应注意该表零点的取法。

（二）热力学第一定律应用于闭口系统中的表达式

根据能量守恒，外界加给系统内工质的热量，等于工质的内能增加和对外界所做的功，对于单位质量的工质，即

对于无损失的可逆过程，对外界的功可表示为

由式（2-12）可知，这个功是由于闭口系统体积的变化所产生的，因此称之为膨胀功。由定积分可知，在p-v图上，膨胀功就是可逆过程曲线与横轴所围的面积，因此p-v图又叫示功图。

（三）动能

流动工质具有一定的速度，因此就具有一定的动能，即

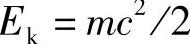
式中，m——物体的质量。

对于1kg工质，其动能即为c²/2。

（四）热力学第一定律应用于开口系统——稳定流动能量方程

所谓稳定流动，是指热力系统在任何截面上工质的一切参数都不随时间而变。稳定流动的条件是：进出口处工质的状态不随时间而变；进出口处工质流量相等且不随时间而变，满足质量守恒条件；系统与外界交换的热和功等一切能量不随时间而变，满足能量守恒条件。

1.稳定流动能量方程式

图2-4所示为一个开口系统的示意图。在该开口系统中，有工质流入流出系统，与此同时，随工质的流入和流出也同时发生着工质带进、带出能量，在系统与外界之间，还发生着功量与热量的交换。

考虑稳定流动的情况，在该控制体内，既不会有能量的积聚，也不会有能量的减少，因而系统的能量是不变的。

为了使问题简化，假定流进、流出系统的工质为1kg。

已知进口截面上，工质的流速为c₁，状态参数为p₁、v₁和T₁。出口截面上流速为c₂，工质状态参数为p₂、v₂和T₂。

工质流入系统时带进的能量有下述几项：工质的内能u₁；工质由于具有流速而带有的动能c²₁/2；工质由于占有一定高度而具有的势能gz₁；工质流入时受其上游流体所做的推进功p₁v₁。

图2-4 开口系统示意图

这样，对于流入系统的1kg工质，随着它的流入，系统获得的能量为

同理，1kg工质流出体系时带出的能量为

另外，设1kg工质流经系统时从外界吸入的热量为q，对外界所做的功为w，根据稳定流动的条件，有

(www.xing528.com)

移项整理后可得

这个式子就是稳定流动能量方程，它是热力学第一定律应用于开口系统的具体形式。

当工质为流体时，比如水轮机用水作为工质的情况，重力势能gz一项很大，不能忽略。当工质为气体时，由于气体的比体积很大，即密度很小，工质流经热力设备时，其所处高度的差别也很小，因此重力势能gz一项与其他各项相比很小，通常可以忽略。

2.焓

在分析开口系统时我们看到，当工质发生流动时，必然存在推进功pv，同时工质必然具有一定的内能，因此对于流动工质，u和pv就是同时存在的。为了计算方便起见，把这两种能量合并在一起，叫做“焓”，1kg工质的焓用h表示，表达式为

任意质量工质的焓用大写字母H表示，即

式（2-15）就是焓的定义式。容易看出，焓的单位与内能相同，为J/kg。由于u、p、v都是状态参数，因此h也是状态参数。

对于理想气体而言。内能u只是温度T的单值函数，而pv=RT，因此有

可见，理想气体的焓只是温度T的函数，即

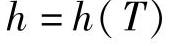
引用焓的概念后，若忽略重力，式（2-14）可以简化为

3.滞止参数

热力设备中工质总是流动着的，因此焓h和速度c总是同时存在的，对于气体来说，h+c²/2就表示流动工质所携带的总能量。

当流速为c₁的气流流经图2-5所示的障碍物时，在正对着来流方向的那一点，流动工质就会由于受到阻碍而速度下降为零，这种现象称为滞止现象。

显然，在上述滞止现象中，工质与外界没有发生热量与功量的交换，因而气流滞止前后的总能量应当相等，滞止点上流速变为零，根据稳定流动能量方程，此时q=0、w=0、c₂=0，因此由式（2-17）可得

图2-5 流动的滞止

当气流被滞止时，气流的动能转变为气流焓值的增加。滞止状态时气流的参数称为滞止参数或总参数。总参数通常用相应静参数的符号上加一个上标*表示，即

引用总焓的概念后，稳定流动能量方程可以进一步简化为

如果系统与外界没有热量交换，这样的过程叫绝热过程，此时q=0，于是有

即总焓的减少转变为对外做功。

如果系统与外界没有功的交换，则w=0，此时有

即外界加给工质的热量全部转变为工质总焓的增加。这一过程称为绝功过程。

如果系统与外界既没有热量的交换，也没有功的交换，这样一个过程称为绝热绝功过程，即绝能过程，则此时有

即气流的总焓不变。