压力修正法与非原始变量法的流场数值计算方法

流场计算的基本过程是在空间上用有限体积法或其他类似方法将计算域离散成许多小的体积单元，在每个体积单元上对离散后的控制方程组进行求解。流场计算方法的本质就是对离散后的控制方程组的求解。通常对离散后的控制方程组的求解可分为耦合式解法（coupled method）和分离式解法（segregated method），归纳后如图1-2所示^[88]。

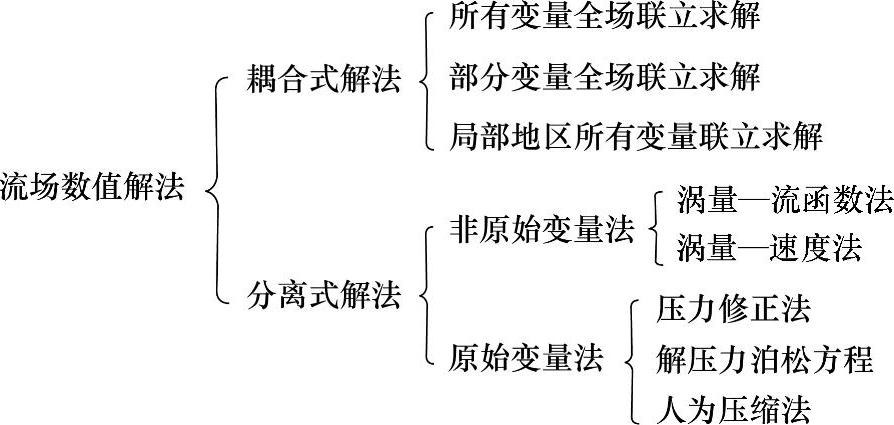
图1-2 流场数值计算方法分类图

1.耦合式解法

耦合式解法同时求解离散化的控制方程组，联立求解出各变量，其求解过程如下：

1）假定初始压力和速度等变量，确定离散方程的系数及常数项等。

2）联立求解连续方程、动量方程、能量方程。

3）求解湍流方程及其他标量方程。

4）判断当前时间步上的计算是否收敛。如不收敛，返回到第2）步，迭代计算。若收敛，重复上述步骤，计算下一步时间步的物理量。

耦合式解法可以分为所有变量整场联立求解（隐式解法）、部分变量整场联立求解（显隐式解法）、在局部地区（如一个单元上）对所有变量联立求解（显式解法）。最后一种求解方法，是在一个单元上求解所有变量后，逐一地在其他单元上求解所有的未知量。这种方法在求解某个单元时，要求相邻单元的变量解是已知的。

当计算中流体的密度、能量、动量等参数存在相互依赖关系时，采用耦合式解法具有很大优势，如求解关于u、v、ρ、T共4个变量的方程组。其主要应用包括高速可压流动、有限速率反应模型等。耦合式解法中，所有变量整场联立求解应用较普遍，求解速度较快，而在局部对所有变量联立求解仅用于声变量动态性极强的场合，如微波捕捉。

假设计算区域内的节点数为N，则每一时间步内需求解4N个方程构成的代数方程组（三个速度方程及一个压力或密度方程）。不足之处是耦合式解法计算效率较低、内存消耗大。

2.分离式解法

分离式解法不直接解联立方程组，而是顺序地、逐个地求解各变量代数方程组。按是否直接求解原始变量u、v、w和p，分离式解法分为非原始变量法和原始变量法。

非原始变量法是取旋度ω和流函数Ψ或旋度ω和原始变量u、v、w作为基本变量的流场数值计算方法。非原始变量法分为涡量-流函数法和涡量-速度法。涡量-流函数法不直接求解原始变量u、v、w和p，而是求解旋度ω和流函数Ψ。涡量-速度法不直接求解流场的原始变量p，而是求解旋度ω和速度u、v、w。这两种方法的本质、求解过程和特点基本一致，共同优点是：方程中不出现压力项，从而避免了因求压力带来的问题。另外，涡量-流函数法在某些条件下，容易给定旋度值，比给定速度值要容易。这类非原始变量法的缺点是：不易扩展到三维情况，因为三维水流不存在流函数；当需要得到压力场时，需要额外的计算；对于固壁面边界，其上的旋度极难确定，没有适宜的固体壁面上的边界条件，往往使涡量方程的数值解发散或不合理。因此，尽管非原始变量的解法巧妙地消去了压力梯度项，且在二维情况下涡量-流函数法要少解一个方程，却未能得到广泛的应用。人们宁可想办法处理压力梯度项，即直接利用原始变量u、v、w和p作为因变量进行求解。(www.xing528.com)

原始变量法是取速度u、v、w和压强p作为基本变量的流场数值计算方法。原始变量法包含的解法比较多，常用的有解压力泊松方程法、人为压缩法和压力修正法。解压力泊松方程法需要对方程取散度等方法处理将动量方程转变为泊松方程，然后对泊松方程进行求解。

人为压缩法主要是根据可压的气体通过联立求解速度分量与密度的求解原理启发，引入人为压缩性和人为状态方程，以此对不可压流体的连续性方程施加干扰，将连续方程嵌入人为密度的基本方程。但这种方法要求时间步长必须很小，因此限制了它的广泛应用。

压力修正法是目前工程上使用较为广泛的流场数值计算方法。压力修正法的实质是迭代法。在每一时间步长的运算中，先给出压力场的假定初始值，据此求出假定的速度场。再求解根据连续方程导出的压力修正方程，对假定的压力场和速度场进行修正。如此循环往复，可得出压力场和速度场的收敛解。其基本思路是：

1）假定初始压力场；

2）利用压力场求解动量方程，得到速度场；

3）利用速度场求解连续方程，使压力场得到修正；

4）根据需要，求解湍流方程及其他标量方程；

5）判断当前时间步上的计算是否收敛。若不收敛，返回到第2）步，继续迭代计算；若收敛，计算下一时间步的物理量。

压力修正法有多种实现方式，其中，压力耦合方程组的半隐式方法（SIMPLE算法）应用最为广泛，也是各种商用CFD软件普遍采纳的算法^[89]。SIMPLE（Semi-Implicit Method for Pressure Linked Equations）算法由Patanker与Spalding于1972年提出^[90，91]，它是一种主要用于求解不可压流场的数值方法，但也被用于计算可压流场。其基本思想被其他数值方法所采纳^[92，93]，所以该方法是目前工程上应用最为广泛的一种流场计算方法，它属于压力修正法的一种。其核心是采用“猜测-修正”的过程，在交错网格的基础上来计算压力场，从而达到求解动量方程的目的。

3.SIMPLE算法的改进

尽管基于原始变量法是目前不可压缩流动问题数值求解中使用最为成熟的一类方法，但是在求解不压缩流体时，都有一个不可回避的问题，即压力-速度耦合问题。由Patanker创建的基于交错网格SIMPLE算法巧妙地解决了这一问题，也解决了很多工程实际问题。但该方法缺点也很明显，因为速度分量u、v、w与压力p存储在不同的节点位置上，求u方程v、w需插值，求v方程u、w需插值，求w方程u、v需插值。此外，为保证u、v、w取值的等价性，需保存u、v、w上次迭代值。不仅u、v、w需插值，如果物性系数在流场中有变化，同样需插值。因此占用的内存大，需进行繁琐的插值^[94-96]。Peric^[97]先后采用非交错网格（同位网格）进行数值求解。为保证压力与速度的耦合，界面速度采用动量插值MI（Momentum Interpolation）^[98]，也称为压力加权插值PWIM（Pressure Weighted Interpolation Method）^[99]。由于动量插值算法是线性插值与动量插值组合而成的一种混合插值^[77]，也就是说流场计算结果或多或少与速度松弛因子有关，为克服PWIM的这一缺点，界面速度更新采用亚松弛计算。还有一种更方便的办法就是在动量方程插值的计算中将动量方程主对角元系数中隐含的松弛因子取为1^[100，101]，该方法目前比较流行。由于界面速度不是线性插值，而是动量插值，因此必须同时存储界面与节点速度。

Date^[102]指出上述两种插值方法不仅不必要，而且在压力变化严重偏离线性时会得到虚假的结果，他提出的直角坐标系中结构化同位网格上全新的压力校正方程，可在粗糙网格上得到光滑的压力场。这种算法简化了编程，占用内存小，因此，是一种更经济的算法，计算时，界面速度、压力均采用算术平均。

本书的SIMPLED算法基本思想与Date相同，不同的是对界面速度和压力的处理方法。由于采用的是非结构化网格，因此对于离心泵的内流CFD计算，Date算法中的算术平均可能会引起不合理的速度场和压力场，因此，需要对界面速度和压力的平均方法重新考虑。而对非结构化网格中心的标量取平均，通常采用以节点到邻点的距离为倒数的加权平均形式^[103]，以减少计算时间，所以，在对压力进行平均时，采用倒数加权平均方法，这也是参考文献[104]、[105]所采纳的方法。与压力相比，速度对计算结果的精度影响更大，综合考虑数学上几种常用的平均方法，对界面速度分别取算术平均、倒数加权平均，但是得到的结果不是很令人满意，从而考虑将界面速度以所在单元的面积为权重作平均加权插值，使场的分布控制在一个合理的范围内，以提高计算精度。