典型例题分析大全

例17-1　图17-1（a）所示为一厚度B=12 mm的钢制凸轮，质量m=1.2 kg，质心S

离轴心的偏心距e=4 mm。为了平衡此凸轮，拟在R=40 mm的圆周上钻3个直径相同且相互错开60°的孔，试求应钻孔的直径（已知钢材密度ρ=7.8×10-6kg/mm3）。

解：由题意可知，此凸轮厚度较小，所以凸轮的平衡为静平衡。凸轮的不平衡质径积为me，每个钻孔的质径积为-m′R，可按去除的钻孔的体积、密度计算出质径积-m′R，即：

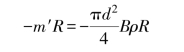
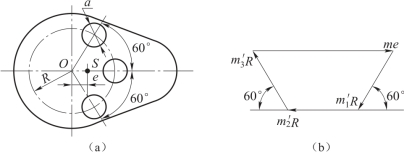
图17-1　例17-1图

下面用向量图解法求解：

取比例尺μW=0.1 kg·mm/mm，根据静平衡条件∑miri=0作向量多边形。由题意可知，me=4.8 kg·mm，且水平向右，按比例尺画出me。三个钻孔的质径积大小相等，并互相错开60°，m′iR的方向与钻孔中心径向相反，如图17-1（b）所示。图17-1中代表m′1R、m′2R和m′3R的线段长度均为24 mm。

由图得到-m′R=-24×μW=-24×0.1=-2.4 kg·mm，代入式（1），可得：

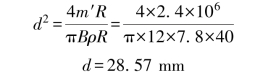
故钻孔直径应为28.57 mm。

例17-2　在如图17-2所示的转子中，已知各偏心质量m1=10 kg，m2=15 kg，m3=20 kg，m4=10 kg，它们的回转半径分别为r1=40 cm，r2=r4=30 cm，r3=20 cm。又知各偏心质量所在的回转平面间的距离为l12=l23=l34=30 cm，各偏心质量的方位角如图17-2所示。若置于平衡基面Ⅰ及Ⅱ中的平衡质量mbI及mbII的回转半径均为50 cm，试求mbI和mbII的大小及方位。

图17-2　例17-2图

解：根据动平衡条件有：

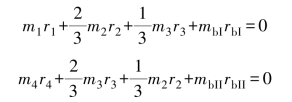
以μW作质径积多边形，如图17-2（b）及图17-2（c）所示。由图可得：

平衡基面Ⅰ：

平衡基面Ⅱ：(www.xing528.com)

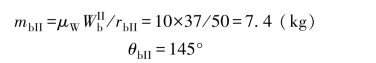
例17-3　某多气缸原动机的等效力矩图如图17-3所示，等效阻力矩Mer为常数，f1，f2，…各块面积所代表的功的绝对值如表17-1所示，等效构件的平均转速nm为120 r/min，运转不均匀系数的许用值为[δ]=0.06，忽略其他构件的转动惯量。试确定飞轮的等效转动惯量JF，并指出最大、最小角速度出现在什么位置。

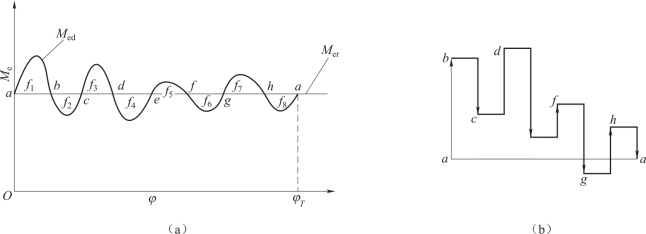
图17-3　例17-3图

表17-1　单元面积代表的盈亏功

解：飞轮转动惯量的计算公式为

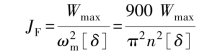
因此，本题的关键是如何正确求出最大盈亏功Wmax，其解法有以下两种。

（1）根据已知各单元面积所代表的盈亏功，先求出Med与Mer各交点处盈亏功的累积变化量（即ΔW），并列于表17-2中。

表17-2　盈亏功的累积变化量

由此可知，D点处ΔW最大，G点处ΔW最小，φd与φg即此系统出现ωmax与ωmin的位置。最大盈亏功为

Wmax=ΔWmax-ΔWmin=650-(-70)=720(J)

（2）用能量指示图求解。具体做法是：开始可任作一水平线为基线，并选一交点为起始点，然后分别按比例用垂直向量表示上述面积，向上为正，向下为负，依次首尾相接，如图17-3（b）所示。图中最高点d和最低点g分别表示机械系统动能最高和最低时的位置，即ωmax与ωmin对应的位置。因此，点d和g间的垂直距离即相当于相应区间内正、负面积代数和的绝对值，故代表最大盈亏功Wmax。由图17-3（b）可知：

与方法（1）的计算结果完全相同。将ΔW代入飞轮转动惯量计算式，可得：

注意：本题是求飞轮转动惯量的典型题型，其关键是求最大盈亏功，求出最大盈亏功后再由公式求出飞轮的转动惯量即可。