一、实验目的
本实验通过对一组螺栓的静载受力分析及单个螺栓的静、动载受力分析,达到以下目的:
1.螺栓组实验
(1)了解托架螺栓组受翻转力矩引起的载荷,对各螺栓拉力分布情况的影响;
(2)根据拉力分布情况,确定托架底板旋转轴线的位置;
(3)将实验结果与螺栓组受力分布的理论计算结果进行比较。
2.单个螺栓静载实验
了解受预紧轴向载荷螺栓连接中,零件相对刚度的变化对螺栓所受总拉力的影响。
3.单个螺栓动载荷实验
通过改变螺栓连接中零件的相对刚度,观察螺栓中动态应力幅值的变化。
二、实验设备
本实验的实验设备是LSC-Ⅱ螺栓组及单个螺栓连接综合实验台。
三、实验原理
1.螺栓组实验台的结构与工作原理
螺栓组实验台的结构如图19-1所示。图中1为托架,在实际使用中多为水平放置,为了避免由于自重产生力矩的影响,在本实验台上设计为垂直放置。托架以一组螺栓3连接于支架2上。加力杠杆组4包含两组杠杆,其臂长比均为1∶10,则总杠杆比为1∶100,可使加载砝码6产生的力放大100倍后压在托架支承点上。螺栓组的受力与应变转换为粘贴在各螺栓中部的应变片8的伸长量,用应变仪来测量。两片应变片在螺栓上相隔180°粘贴,输出串接,以补偿螺栓受力弯曲引起的测量误差,引线由孔7中接出。

图19-1 螺栓组实验台
1—托架;2—支架;3—螺栓;4—杠杆组;5—底座;6—加载砝码;7—引线孔;8—应变片
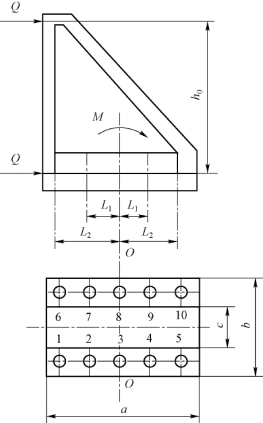
图19-2 螺栓组的布置
如图19-2所示,加载后,托架螺栓组受到一横向力及力矩,与接合面上的摩擦阻力相平衡。而力矩使托架有翻转趋势,使得各个螺栓受到大小不等的外界作用力。根据螺栓变形协调条件,各螺栓所受拉力F(或拉伸变形)与其中心线到托架底板翻转轴线的距离L成正比。即

式中,F1、F2为安装螺栓处由于托架所受力矩而引起的力(N);L1、L2为从托架翻转轴线到相应螺栓中心线间的距离(mm)。
本实验台中第2、4、7、9号螺栓下标为1;第1、5、6、10号螺栓下标为2;第3、8号螺栓到托架翻转轴线的距离为零(L=0)。根据静力平衡条件可得:
![]()
![]()
式中,Q为托架受力点所受的力(N);h0为托架受力点到接合面的距离(mm),如图19-2所示。
本实验中取Q=3500N,h0=210mm,L1=30mm,L2=60mm。
把式(19-1)代入式(19-3)中,则第2、4、7、9号螺栓的工作载荷为

第1、5、6、10号螺栓的工作载荷为

2.螺栓预紧力的确定
本实验是在加载后不允许连接接合面分开的情况下来预紧和加载的。在预紧力的作用下,连接接合面产生的挤压应力为

悬臂梁在载荷力Q的作用下,若要使接合面不出现间隙,则应满足

式中,Q0为单个螺栓预紧力(N);Z为螺栓个数,Z=10;A为接合面面积,A=a(b-c)(mm2);W为接合面抗弯截面系数,其计算公式如下:

本实验中取a=160mm,b=105mm,c=55mm。
由式(19-6)、式(19-7)及式(19-8)可知:

为保证一定的安全性,取螺栓预紧力

下面我们再分析螺栓的总拉力。
在翻转轴线以左的各螺栓(1、2、6、7号螺栓)被拉紧,轴向拉力增大,其总拉力为

或

在翻转轴线以右的各螺栓(4、5、9、10号螺栓)被放松,轴向拉力减小,总拉力为
 (https://www.xing528.com)
(https://www.xing528.com)
或

式中, 为螺栓的相对刚度,CL为螺栓刚度,CF为被连接件刚度。
为螺栓的相对刚度,CL为螺栓刚度,CF为被连接件刚度。
螺栓上所受到的力是通过测量应变值而计算得到的。根据虎克定律:
![]()
式中,ε为变量,σ为应力(MPa),E为材料的弹性模量,对于钢材,取E=2.06×105MPa。
螺栓预紧后的应变量为

则由式(19-15)可得螺栓受载后总应变量

或
![]()
式中,d为被测处的螺栓直径(mm),K为系数,![]()
因此,可得到在翻转轴线以左的各螺栓(1、2、6、7号螺栓)的工作拉力为
![]()
在翻转轴线以右的各螺栓(4、5、9、10号螺栓)的工作拉力为

3.单螺栓连接实验台的结构及工作原理
单螺栓连接实验台部件的结构如图19-3所示。旋动调整螺帽1,通过支持螺杆2与加载杠杆8,可使吊耳3受拉力载荷,吊耳3下有垫片4,改变垫片材料可以得到螺栓连接的不同相对刚度。吊耳3通过被测单螺栓5、紧固螺母6与机座7相连接。小电机9的轴上装有偏心轮10,当电机轴旋转时由于偏心轮转动,通过杠杆使得吊耳和被测单螺栓上产生一个动态拉力。吊耳3与被测单螺栓5上都贴有应变片,用于测量其应变的大小。变应力幅值调节手轮12可以改变小溜板的位置,从而改变动拉力的幅值。
四、实验方法及步骤
1.螺栓组实验
(1)在实验台螺栓组各螺栓不加任何预紧力的状态下,将各螺栓对应的半桥电路引线(1~10号线)按要求接入所选用的应变仪相应接口中,根据应变仪使用说明书进行预热(一般为三分钟)并调平衡。
(2)由式(19-10)计算出每个螺栓所需的预紧力Q0,并由式(19-16)计算出螺栓的预紧应变量ε0,并将结果填入表19-1中。
(3)按式(19-4)、式(19-5)计算每个螺栓的工作拉力Fi,将结果填入表19-1中。
(4)逐个拧紧螺栓组中的螺母,使每个螺栓的预紧应变量约为ε0。各螺栓应交叉预紧,为使每个螺栓的预紧力尽可能一致,应反复调整2~3次。
(5)对螺栓组连接进行加载,加载力为3500N,其中砝码连同挂钩的重量为3.754kg。停歇两分钟后卸去载荷,然后再加上载荷,在应变仪上读出每个螺栓的应变量εi,填入表19-2中,反复做3次,取3次测量值的平均值作为实验结果。
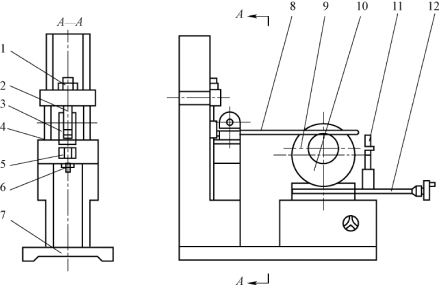
图19-3 单个螺栓实验台
1—螺帽;2—螺杆;3—吊耳;4—垫片;5—被测螺栓;6—紧固螺母;7—机座;8—加载杠杆;9—小电机;10—偏心轮;11—预紧或加载手轮;12—变应力幅值调节手轮
(6)画出实测的螺栓应力分布图。
(7)用机械设计中的计算理论计算以上各测量值,绘出螺栓组连接的应变图,并与实验结果进行对比分析。
2.单个螺栓静载实验
(1)旋转调节手轮12的摇手,移动小溜板至最外侧位置。
(2)如图19-3所示,旋转紧固螺母6,预紧被测螺栓5,预紧应变为ε0=500με。
(3)旋动调整螺帽1,使吊耳3上的应变片(12号线)产生ε=50με的恒定应变。
(4)换用不同弹性模量材料的垫片,重复上述步骤,将螺栓总应变εi记录在表19-3中。
(5)用下式计算刚度Ce,并作不同垫片实验结果的比较分析。

式中,A为吊耳测应变的截面面积,本实验中A为224mm2;A′为试验螺杆测应变的截面面积,本实验中A′为50.3mm2。
3.单个螺栓动载荷实验
(1)安装吊耳下的钢制垫片。
(2)将被测螺栓5加上预紧力,预紧应变仍为ε0=500με(可通过11号线测量)。
(3)将加载偏心轮转到最低点,并调节调整螺母1,使吊耳应变量ε=5~10με(通过12号线测量)。
(4)开动小电机,驱动加载偏心轮。
(5)从波形线上分别读出螺栓的应力幅值和动载荷幅值,将结果填入表19-4中。
(6)换上环氧垫片,移动电机位置以改变被连接件的刚度,调节动载荷的大小,使动载荷幅值与使用钢垫片时相一致。
(7)估计地读出此时的螺栓应力幅值,将结果填入表19-4中。
(8)作不同垫片下螺栓应力幅值与动载荷幅值关系的对比分析。
(9)松开各部分,卸去所有载荷。
(10)校验电阻应变仪的复零性。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




