纯液体条件下液力透平内部流场计算优化

1.计算模型

本节以一组单级离心泵反转作液力透平为研究对象，这些离心泵的基本参数如表11⁃1所示。

表11⁃1 泵的基本参数

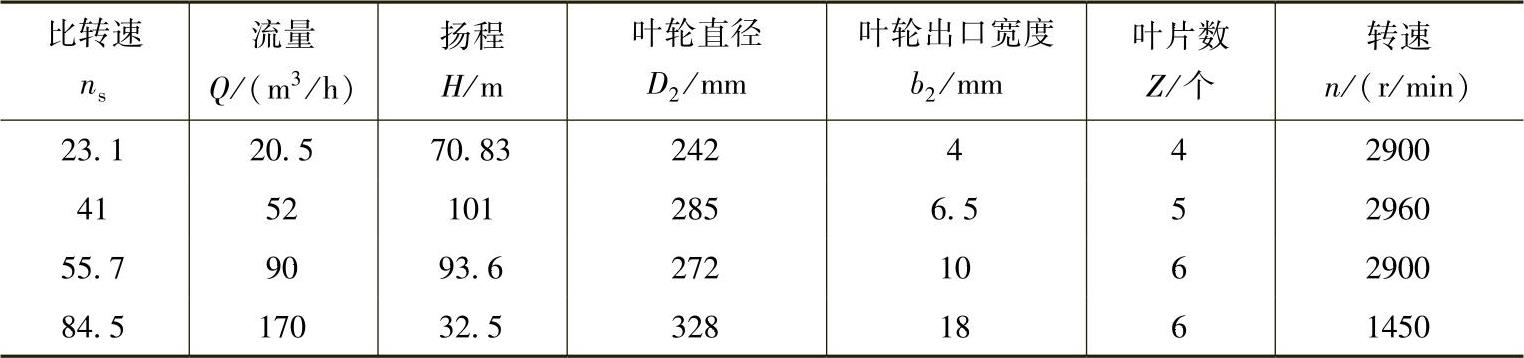
在离心泵反转作液力透平时，叶轮进口成为液力透平叶轮的出口，叶轮出口成为液力透平叶轮的进口，蜗壳进口成为液力透平蜗壳的出口，蜗壳出口成为液力透平的进口。

2.液力透平叶轮和蜗壳的建模

液力透平的叶轮是完成液体输送的主要部件，而叶片的造型是整个实体模型建立过程中的难点和重点。一方面叶片形状复杂，扭曲严重，且厚度不均匀；另一方面它是液力透平的核心，与液力透平的水头、流量、效率和特性曲线的形状等有着重要关系。利用FLUENT自带的前处理软件Gambit建模困难较大，且光滑性不好，所以为了保证模型的质量，本节采用专业的Pro/Engineer软件建模。

液力透平叶轮的建模过程如下[73]：

1）首先选择旋转轴为Z轴。以叶轮轴面投影图的外部轮廓为母线，以Z轴为旋转中心，应用Pro/Engineer的旋转功能生成叶轮的轮廓实体，即包括叶轮前后盖板的整体形状。

2）选择圆柱坐标系，使用偏移坐标系基准点命令，分别输入每条等包角度的木模截线坐标点；用插入基准曲线命令，将每条等包角度木模截线坐标点分别连接起来，并使用曲面混合命令将曲线连接起来，便生成了叶片的工作面和背面；使用面合并命令，将叶片的面两两合并，最终成为一个封闭的曲面。

3）由于叶轮有数个叶片，所以将做好的一个叶片进行选择性复制粘贴，得到一个叶轮的全部叶片。

4）最后用面合并命令分别将每个叶片和叶轮的前后盖板进行合并，合并时去除叶片，保留流道。再对整个叶轮进行实体化，就得到了叶轮的全流道模型。

液力透平蜗壳模型的建立过程

1）选择和叶轮建模时相同的旋转轴作为蜗壳旋转中心线；

2）根据水力图，草绘出蜗壳的8个断面；

3）使用扫描混合的方法直接生成蜗壳的第1至第8断面部分；

4）草绘出蜗壳的第9、第10断面，使用扫描混合命令生成扩散段部分；

5）最后使用倒圆角命令生成隔舌。

将液力透平的叶轮和蜗壳进行装配，组装到一起即得到了液力透平的整体计算区域。本文所选的4台不同比转速的液力透平的模型如图11⁃4所示。

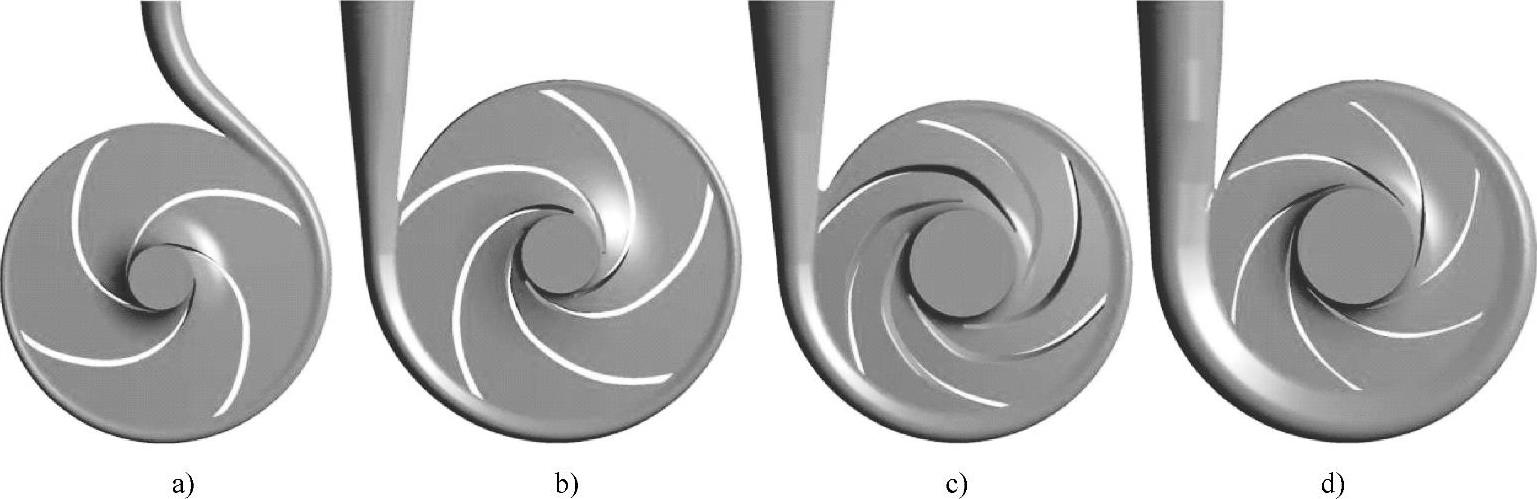
图11⁃4液力透平计算区域模型

a）n_sp=23.1 b）n_sp=41 c）n_sp=55.7 d）n_sp=84.5 （彩图见书后插页）

3.网格划分和质量检查

为了对创建的模型进行模拟仿真，在几何模型内建立高质量的网格是必不可少的。数值模拟所采用的网格类型主要有结构化网格、非结构化网格、分块结构化网格和自适应笛卡儿网格等几种[67]。

本节采用FLUENT的前处理软件Gambit进行网格划分。Gambit提供了多种网格单元，可根据用户的要求自动完成网格划分的工作，并且可以生成结构网格、非结构网格和混合网格等多种类型的网格。它有着良好的自适应功能，能对网格进行细分和粗化，或生成不连续网格、可变网格和滑移网格，并且与分析软件FLUENT匹配较好。由于液力透平叶轮叶片形状扭曲，故本节采用对复杂边界适应性很强的非结构化四面体混合网格。网格划分好后对网格质量进行检查。四种比转速液力透平计算区域的网格划分结果如图11⁃5所示。

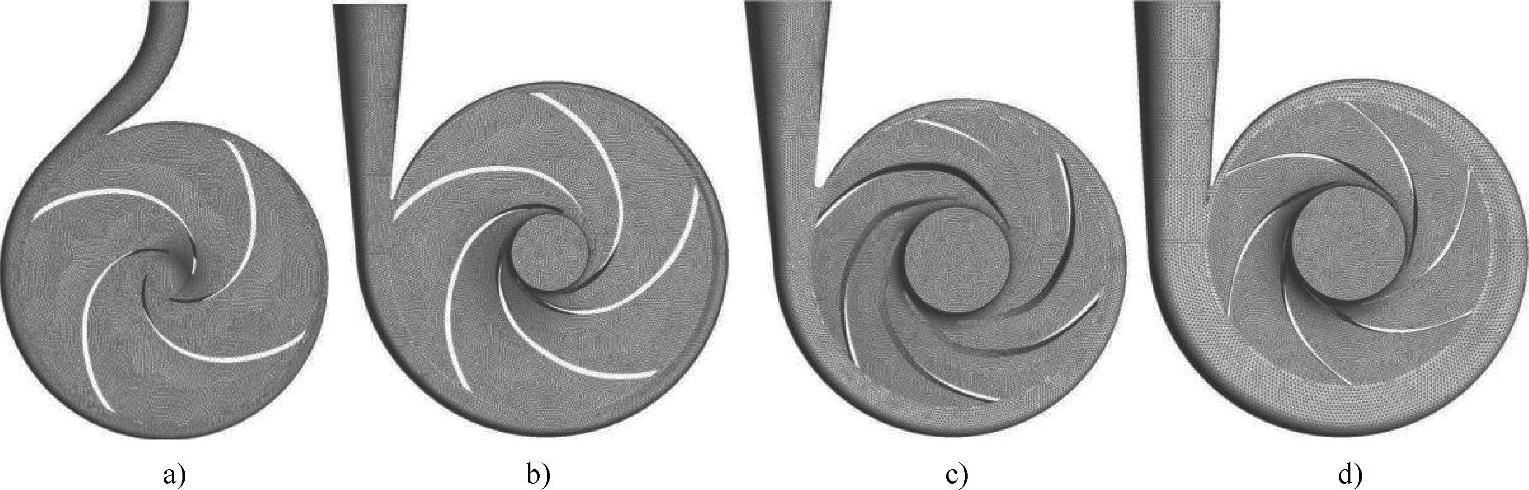
图11⁃5 液力透平计算区域网格

a）n_sp=23.1 b）n_sp=41 c）n_sp=55.7 d）n_sp=84.5 （彩图见书后插页）

对生成的网格的品质进行检查是很重要的，因为类似失真等问题会严重影响FLUENT计算的准确性。网格质量将影响单元间的通量计算，因此直接影响计算的精度和收敛的难易程度。一个高质量网格的判断标准有很多，常用的是EquiAngleSkew和EquiSizeSkew[74]。EquiAngleSkew是通过单元夹角计算的歪斜度，在0～1之间，0表示质量最好，1表示质量最差，最好控制在0～0.4之间。EquiSizeSkew是通过单元大小计算的歪斜度，在0～1之间，0表示质量最好，1表示质量最差。对于质量好的2D单元，该值最好在0.1以内，3D单元在0.4以内。在FLUENT软件中，用Grid/Check命令检查网格的质量。

另外网格数量对计算结果也有一定的影响，网格数量过少或过多会偏离最优的计算结果。为了消除网格数量的影响，本节对比转速为23.1、41、55.7、84.5的4种液力透平都进行了网格无关性检查。下面以比转速为84.5的液力透平网格划分为例说明网格无关性的检查过程。不同网格数目下的计算结果比较见表11⁃2，收敛精度为0.0001。

表11⁃2 不同网格数时计算结果比较

由上表可知，随着网格数量的增加，透平的水力效率先是递增，达到一个最大值后就减小，这说明在划分网格时除了保证网格质量外，网格数量也要确定一个合适的值。网格质量可以影响数值计算的效率和精确度；网格数量则影响计算结果的准确度，网格的无关性检查很是必要。同时，网格数量较大时，计算所消耗的时间也相应增长，对计算机性能的要求更高。因此，为了得到可靠的结论，且充分利用资源，需要对网格数量进行合理的选择。(www.xing528.com)

4.湍流模型的选择

液力透平属于旋转机械，其内部流动是经过充分发展的高雷诺数湍流，流场中物理量具有脉动特性，为了考察脉动的影响，目前广泛采用的方法是时间平均法。该方法是将湍流看作两个流动的叠加，一个是时间平均流动，另外一个是瞬时脉动流动，这样就把脉动项从整体流动中“分离”出来，便于进一步的处理和分析。

湍流的数值模拟有直接数值模拟和非直接数值模拟两种方式。直接数值模拟是不对湍流流动作简化处理，直接进行求解，能够得到相对较准确的数值解，但目前限于计算机的处理能力及硬件水平，对于三维复杂流场的模拟还不能直接进行求解；而非直接数值模拟时需要对湍流流动作一定程度的简化处理，使得求解变得相对简单，而且计算结果能够较为准确地反映湍流流动事实。非直接数值模拟的主要方法有雷诺（RANS）平均法、大涡模拟（LES）方法和统计平均法。

根据相关文献对于液力透平数值计算时采用的湍流模型以及不同的湍流模型对于液力透平数值计算的适用性情况[11，75，76]，本书选用的湍流模型是标准κ-ε湍流模型。

5.控制方程的离散方法

本书对于液力透平内部流场的数值计算采用的是有限体积法对湍流标准κ-ε方程组进行离散化。另外，在离散化过程中涉及离散格式的构造，所谓的离散格式，就是控制体界面上物理量及其导数的节点的插值方式。常用的离散格式有：中心差分格式、迎风格式、混合格式、指数格式、quick格式等[67]，考虑到本书中液力透平的流场是复杂的三维流场，在求解过程中需要保证相容性、稳定性和收敛性的统一。因此选择相对稳定的迎风格式来求解。

6.初始条件与边界条件设定

初始条件和边界条件是偏微分方程（组）有确定解的前提条件[77]，流体控制方程（N⁃S方程）是偏微分方程组，因此在求解N⁃S方程时，初始条件和边界条件不仅是方程有解的前提，而且初始条件和边界条件给定的合理与否直接关系着方程解的收敛性和精确性。

边界条件根据计算域边界上所求解变量或其导数随时间和地点的变化规律给定。本书对于所研究液力透平给定的边界条件如下：

进口边界条件：FLUENT中提供的进口边界条件有：速度进口（用于不可压流）、压力进口（用于可压或不可压流动）和质量流量进口（只用于可压流动），本章中的流体介质为水，属于不可压流体，因此可选择的进口边界条件有速度进口和压力进口，本书最终选择的是速度进口边界条件，进口处的速度值可以通过液力透平具体所处的工况及进口的过流面积来计算获得。

出口边界条件：FLUENT中提供的出口边界条件有：自由出流、压力出口和压力远场。自由出流不可用于可压流动，同时也不可与压力进口一起使用；压力远场只用于可压流动。结合速度进口边界条件，可用作出口边界条件的是自由出流或压力出口，但考虑到实际液力透平出口需要一定的压力，该压力是为了保证后续流程的正常运行，因此将液力透平出口的边界条件设置为压力出口（按具体要求设压力值）。

壁面条件：液力透平的壁面包括进口延伸段壁面、蜗壳壁面、叶轮壁面（叶片表面、叶轮前后盖板表面）和尾水管壁面，其中叶轮壁面相对于绝对坐标系做旋转运动，其他的壁面相对静止。由于湍流在近壁面区域演变为层流，为了准确地描述流体的流动状态，需要对固壁以及近壁区域做出相应的处理。通常，固壁上采用FLUENT默认的无滑移边界条件，在近壁面区域采用标准的壁面函数。

7.液力透平内部流动的计算策略

本书采用FLUENT软件对液力透平内部流动进行数值计算，其中湍流模型选用的是标准κ-ε两方程模型。边界条件为速度进口，压力出口，固壁采用无滑移壁面条件，近壁区域使用标准的壁面函数处理，有数据传递的交界面设置为interface边界条件。采用有限体积法对控制方程组进行离散，离散格式是二阶迎风格式。

在采用FLUENT数值计算过程中，采用如下的收敛准则：

1）所有残差值小于10^-4。

2）透平进出口质量流量的差值控制在0.5%以内，即满足质量守恒。

8.计算结果分析

（1）不同比转速液力透平内的静压力分布如图11⁃6所示为比转速为23.1、41、55.7、84.5四种泵的透平工况在纯液体条件下液力透平中间截面上蜗壳与叶轮内部的静压分布云图，此时的流量为最优工况流量Q_v，bep。由图11⁃6可知，在不同比转速下，液力透平内部的压力从蜗壳进口到叶轮出口递减，叶片工作面压力大于叶片背面压力。对于每一种比转速的液力透平，在叶轮各流道中，压力分布不完全对称，压力沿流线和过水断面形成线的变化不均匀。还可以看出液力透平的比转速越大时，叶轮中的压力分布越均匀，各流道的压力分布趋于对称，压力沿流线和过水断面形成线的变化更加均匀，压力梯度变化也更加均匀。这说明较大比转速的液力透平内部流动特性较好。

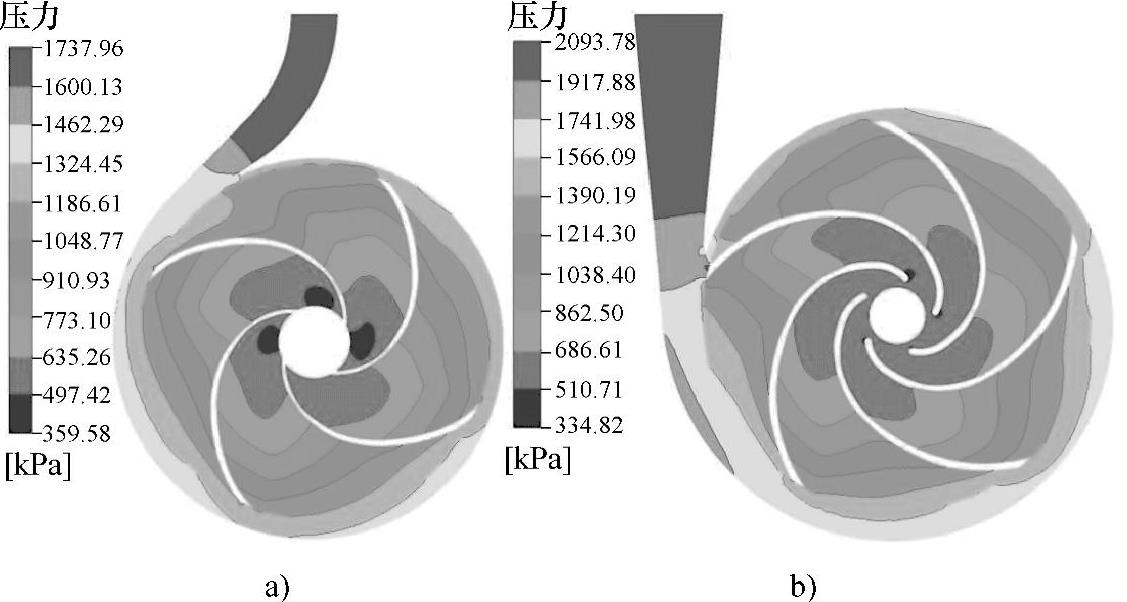
图11⁃6 不同比转速下液力透平内的静压分布

a）n_sp=23.1 b）n_sp=41 （彩图见书后插页）

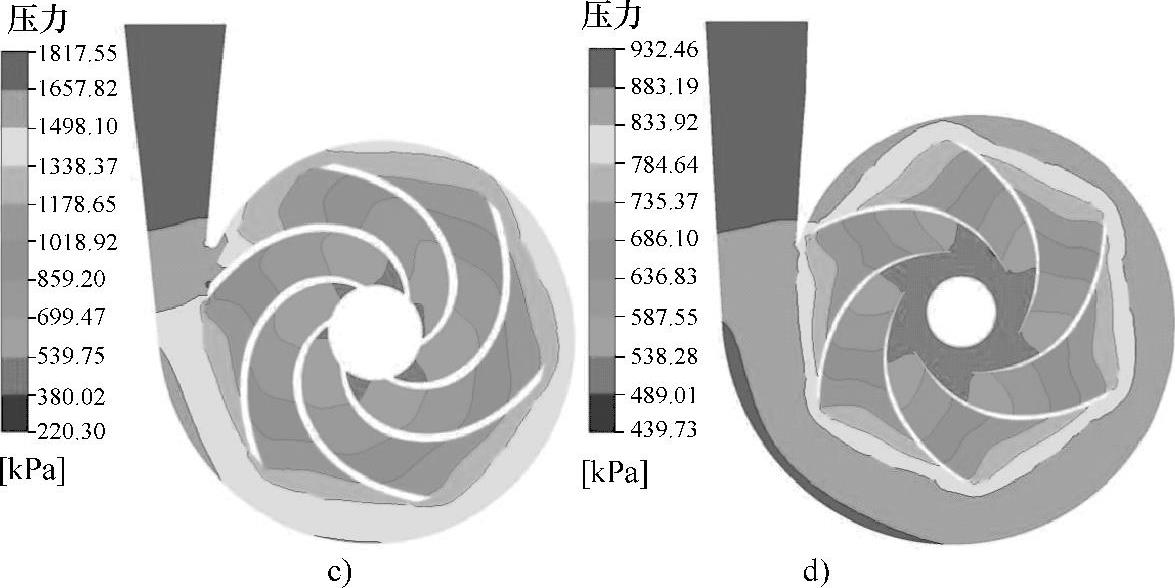
图11⁃6 不同比转速下液力透平内的静压分布（续）

c）n_sp=55.7 d）n_sp=84.5 （彩图见书后插页）

（2）不同比转速液力透平内的速度矢量分布如图11⁃7所示比转速为23.1、41、55.7、84.5四种泵的透平工况在纯液体条件下液力透平中间截面上的相对速度矢量图，此时的流量为最优工况流量Q_v，bep。由图11⁃7可以看出，对于不同比转速的泵反转作液力透平时流道内的流动较为紊乱，且比转速越低时，透平内的流动越发紊乱，随着比转速的增加，透平叶轮内的流动有所改善。比转速为23.1、41时，透平的叶片工作面进口处有一个旋转方向和叶轮旋转方向相同的漩涡区域，并形成较大的回流。叶片背面存在两个较大的、方向相反的漩涡区域，沿着叶轮的旋转方向，叶片背面的两个漩涡逐渐变成一个漩涡，漩涡区域也逐渐减小。比转速为55.7、84.5时，透平叶片工作面形成的漩涡很小，漩涡方向也和叶轮的旋转方向相同，沿着叶轮的旋转方向，漩涡区域逐渐变小。

图11⁃7 不同比转速下液力透平内的速度矢量分布

a）n_sp=23.1 b）n_sp=41 （彩图见书后插页）

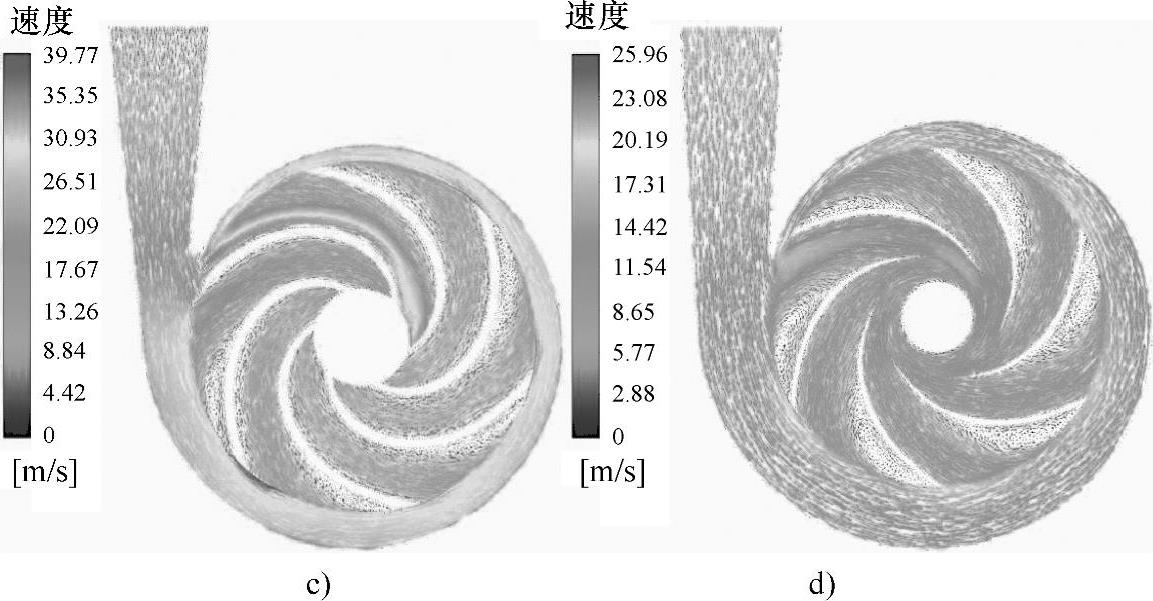
图11⁃7 不同比转速下液力透平内的速度矢量分布（续）

c）n_sp=55.7 d）n_sp=84.5 （彩图见书后插页）