CFD基础理论简介

1.流动控制方程及求解方法

湍流是自然界非常普遍的流动类型。湍流运动的特征是在运动过程中流体质点具有不断的相混掺的现象，速度和压力等物理量在时间和空间上均具有随机的脉动值。无论层流还是湍流，三维瞬态的N⁃S方程都是适用的，而且流体流动要受物理守恒定律支配，基本的守恒定律包括：质量守恒定律、动量守恒定律和能量守恒定律。如果流动包含不同成分的混合和相互作用，系统还要遵守组分守恒定律。如果流动处于湍流状态，还要遵守附加的湍流输运方程。控制方程（Governing Equations）是这些守恒定律的数学描述。

（1）质量守恒方程（连续性方程）任何流动问题都必须满足这种质量守恒定律，在直角坐标系下可得到微分形式的方程

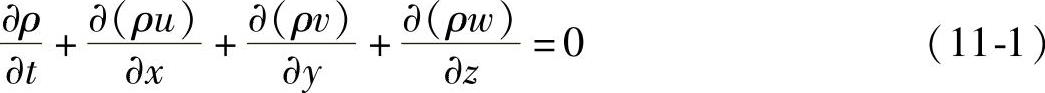
对于不可压缩均质流体，密度为常数，则有

（2）动量守恒方程（运动方程）动量守恒方程也称为N⁃S方程，即

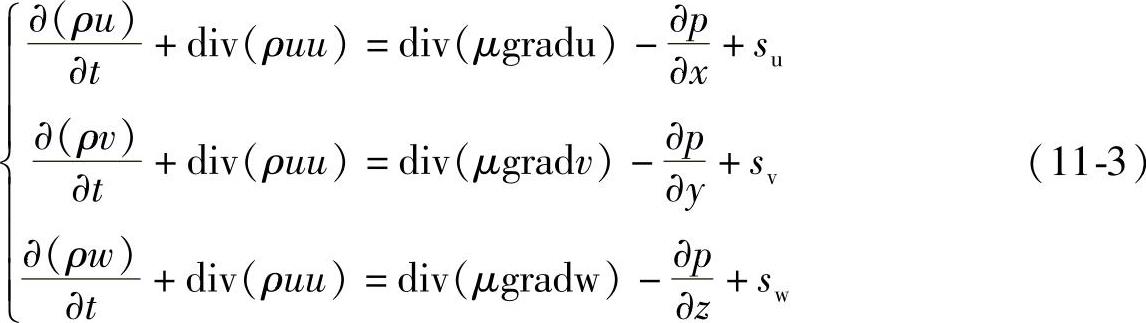
式中 s_u、s_v、s_w——动量守恒方程的广义源项；

μ——动力黏度。

（3）能量守恒方程

式中 k——流体的热传导系数；

c_p——质量比定压热容；

S_T——流体内热源及由于黏性作用流体机械能转化为热能的部分。

（4）组分质量守恒方程（组分方程）流体存在浓度差时，则会有物质的输送，即存在质量的交换，对应有组分质量守恒方程

式中 D_s——该组分的扩散系数；

c_s——组s的体积浓度；

S_s——系统内部单位时间内单位体积通过化学反应产生的该组分的质量，

即生产率。

对于湍流，如果直接求解三维瞬态的控制方程，需要采用直接模拟方法，但这对计算机的内存和速度要求都很高，很难在实际工程中采用。工程上广泛采用的方法是对瞬态N⁃S方程进行时均化，同时补充反映湍流特性的其他方程，组成封闭方程组再进行求解。目前对湍流研究的数值模拟方法主要有四种：

1）DNS直接数值模拟方法：直接求解三维非稳态的N⁃S方程，从模型层次角度看，该模型完全精确，理论上可获得精确解，但受计算条件所限，尚无法用于工程计算。

2）PDF概率密度函数法：从统计的角度进行湍流场信息的描述，是一种很有潜力的模型，但工程应用还有一定距离。

3）RANS雷诺时均N⁃S方程方法：是流场平均变量的控制方程，其相关的模拟理论被称为湍流模式理论。此理论假定湍流中的流场变量由一个时均量和一个脉动量组成，以此观点处理N⁃S方程可以得出雷诺时均N⁃S方程。在引入Boussinesq假设（即认为湍流雷诺应力与应变成正比）之后，湍流计算就归结为对雷诺应力和应变之间的比例系数（即湍流黏性系数）的计算。此方法是目前进行液力透平内部流动数值模拟广为采用的方法。

4）LES大涡模拟：是一种介于DNS和湍流模式之间的一种直接数值模拟的方法，用非稳态N⁃S方程直接求解湍流中的大涡，而小涡的影响采用近似模型来模拟。这种方法对计算机资源的要求低于DNS方法，在理论上比湍流模式理论也更加精确，但因为LES需要使用高精度的网格，对计算机资源的要求仍比较高，所以还不能在工程上被广泛应用。在绝大多数情况下，湍流计算还要采用湍流模式理论，LES方法可以在计算资源足够丰富的时候尝试使用。

2.求解问题的计算模型

在形成了CFD数学模型（控制方程）后，要通过下述环节形成所求解问题的计算模型：计算模式、计算域的数值离散方法、空间离散格式、时间域离散格式、时间积分步长、流场数值算法、几何模型、计算网格、边界条件、初始条件、MKF、滑移网格、动网格等。

（1）计算模式所谓计算模式就是决定流场是定常还是非定常（稳定流还是非稳定流）、单相流还是多相流、流体是否有黏性、有无离散相、温度变化是否需要考虑等。对于液力透平的起动、关机过程以及压力脉动等特性的分析，均属于非定常分析，即需要考虑时间因素的影响。对于液力透平在稳定工况下运行特性的分析，一般只需要作定常计算，即在控制方程中不考虑时间因素，从而可大大降低计算量。

（2）离散方法及离散格式计算域的数值离散方法是指变量在离散节点之间的分布假设及相应推导离散方程的方法。常用的方法有有限差分法、有限元法和有限体积法，近年来使用最广泛的是有限体积法。FLUENT、STAR⁃CD和CFX都是常用的基于有限体积法软件，它们在流动、传热传质、燃烧和辐射等领域应用广泛。

在时间域和空间域将原本连续的控制方程转化为离散方程，是实现CFD计算的第一步，也是决定后续算法精度与效率的重要环节。空间离散格式是在空间域（网格）上建立离散方程时采用的插值方式，常用的离散格式有中心差分格式、一阶迎风格式、二阶迎风格式、乘方格式、QUICK格式等。在FLUENT中，默认情况下，当使用分离求解器时，所有方程中的对流项均用一阶迎风格式离散；当使用耦合求解器时，流动方程使用二阶精度的格式，其他方程使用一阶精度格式进行离散。当流动与网格对齐时，如使用四边形或六面体网格模拟层流流动，使用一阶精度离散是可以接受的，但当流动斜穿网格线时，一阶精度格式将产生很大的离散误差。因此，对于二维三角形网格和三维四面体网格，要使用二阶精度格式，特别对复杂流动更是如此。有时为了加快计算速度，可先在一阶精度下计算，然后再转到二阶精度格式下计算；如果使用二阶精度格式遇到难于收敛的情况，才考虑一阶精度格式。

时间积分格式是指在时间域上积分控制方程时所使用的格式，常用的有显式、半隐式、全隐式等。显式格式要求时间步长较小，但计算效率高，而隐式格式一般需要解方程组。此外，时间积分格式是与所求解的物理问题相关的。对于瞬态问题，尤其是时间步长不受计算稳定性限制的情况，应用最广泛的离散格式是全隐式方案。

（3）数值算法流场数值算法本质上是指离散方程组的解法，主要有耦合式解法和分离式解法，具体分类如图11⁃2所示。

一种常用的分离式解法是基于原始变量模式的压力修正算法，即SIMPLE算法，意为求解压力耦合方程组的半隐式方法。此外，还有改进SIMPLE算法（如SIMPLEC算法）及PISO算法等。PISO算法在分析瞬态问题时优势更突出一些。

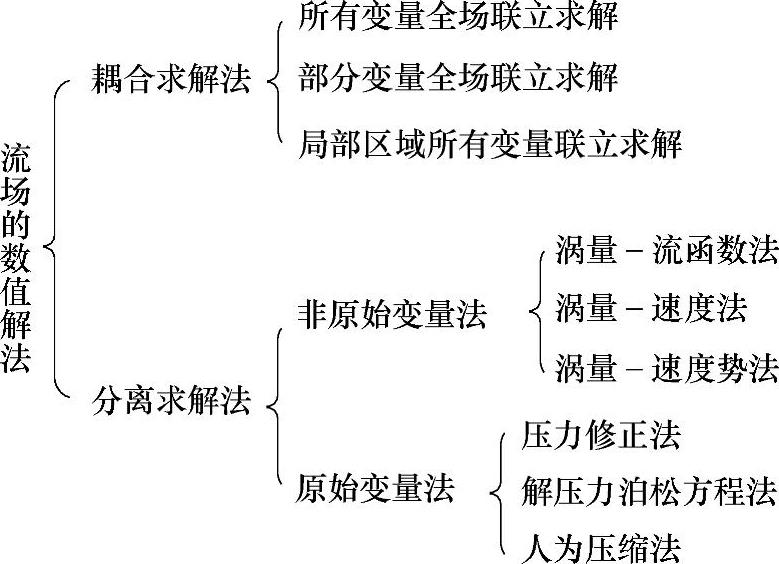
图11⁃2 流场数值计算方法分类

液力透平内部流动通常是作为不可压缩流体流动来处理的，SIMPLE系列算法是目前求解不可压缩流体流动的最主要方法。

（4）几何模型和网格划分几何模型是指针对计算域，采用CAD软件构造的实体模型。实际计算的计算域，往往需要在物理域的基础上作适当延伸。

网格生成是数值计算中一个重要的前处理过程，即在计算域上进行剖分形成小的单元。网格生成大致可以分为两大类：结构化网格和非结构化网格。所谓结构化网格就是网格拓扑，相当于矩形区域内均匀的网格，可以方便准确地处理边界条件，计算精度高，并且可以采用许多高效隐式算法和多重网格法，计算效率也较高。缺点是对复杂外形的网格生成较难，甚至难以实现，即使能生成多块结构化网格，块与块之间的界面处理也十分复杂，因而在使用上受限制。非结构化网格就是指网格单元和节点彼此没有固定的规律可循，其节点分布完全是任意的，其基本思想是任何空间区域都可以被四面体（三维）或三角形（二维）单元所填满，即任何空间区域都可以被划分。但是在实际应用时，非结构化网格的生成，特别是三维情况，是十分耗时的烦琐工作，而且目前与之相结合的有限差分格式也有待进一步优化。

网格品质的好坏直接影响到数值解的精度和计算的稳定性。从理论上讲，网格单元越小，即网格越密，计算精度越高。实际计算时，往往在流场压力梯度或速度梯度比较大的地方，进行局部加密处理。此外，为了提高解的精度，网格点必须足够密，而整体加密网格所增加的计算量是无法忍受的，因此可以作网格的自适应处理。因为非结构化网格的自适应处理很方便，使得自适应网格成为数值计算中提高计算效率和求解精度的一种重要手段。

一般说来，在大梯度的区域，像剪切层或混合域中，网格应该足够密集，使得在单元的流动变量中的变化减到最小。但大多数复杂的三维流动中的网格划分将受到CPU和计算机资源的局限。虽然随着网格的增多，求解的准确性提高，但是求解和结果的处理对CPU和内存的要求也相应提高了。

（5）边界条件边界条件是求解任何物理问题都要设定的，常用的有速度进口、压力进口、壁面、出口等。选择正确的边界条件是得到正确计算结果的关键。选择边界条件虽然看似简单，但准确给定复杂问题的边界条件并不是一件容易的事，需要通过积累经验才能够熟练地选择正确的边界条件。初始条件是非定常（瞬态）问题所必须输入的内容，以表征各物理量在初始时刻的取值。初始条件是所研究对象在过程开始时刻各个求解变量的空间分布情况。对于瞬态问题，必须给定初始条件，对于定常流动问题，不需要初始条件。

以下以软件FLUENT为例说明常用的几个边界条件。

1）速度进口：此边界条件用入口处流场速度及相关流动变量作为边界条件。需要注意的是，因为这种条件中允许驻点参数任意浮动，所以速度入口条件仅使用于不可压缩流，如果用于可压流则可能导致非物理解。同时还要注意的是，不要让速度入口条件过于靠近入口内侧的固体障碍物，这样会使驻点参数的不均匀程度大大增加。

2）压力出口：此边界条件在流场出口边界上定义静压。在压力出口边界上还需要定义“回流（backflow）”条件。回流条件是在压力出口边界条件上出现回流时使用的边界条件。推荐使用真实流场中的数据作为回流条件，这样计算将更容易收敛。在压力出口边界上，FLUENT用Gauge Pressure（表压）栏中的压力作为静压，其他变量则由流场内部插值获得。

3）出流：如果在流场求解前，流场出口处的流动速度和压力是未知的，就可以使用出流边界条件（outflow boundary conditions）。需要注意的是下列情况不适合采用出流边界条件：

①如果计算中使用了压力入口条件的话，应该同时使用压力出口条件；

②流场是可压缩流时；

③在非定常计算中，如果密度是变化的，则不适用出流边界条件；

④在出流边界存在很大的法向梯度，或者出现回流时不应使用此边界条件。

4）壁面边界条件：在黏性流动计算中，FLUENT使用无滑移条件作为默认。在壁面有平移或转动时，也可以定义一个切向速度分量，或定义剪应力作为边界条件。壁面上需要输入的参数如下：

①在移动或转动壁面计算中的壁面运动条件；

例如当壁面有旋转运动时，选择旋转选项并确定转动轴的旋转速度，就可以将壁面的旋转运动唯一确定下来；

②滑移壁面中的剪切力条件；

③湍流计算中的壁面粗糙度；

④粗糙度常数C_s，主要取决于粗糙颗粒的类型，FLUENT系统默认为C_s=0.5，在与κ⁃ε模型混合使用时，C_s的默认值可以准确地计算均匀沙粒型粗糙度。在粗糙度的类型与均匀沙粒相距甚远，以致计算结果出现很大偏差时，可以调整C_s的取值。比如对于非均匀沙粒、肋板等粗糙度的设置，C_s在0.5～1.0之间进行选择。需要注意的是，没有必要让壁面附近的网格尺度小于粗糙度高度。为了获得最好的计算结果，需要保证从壁面到网格几何中心的尺寸大于粗糙度高度。(www.xing528.com)

5）边界条件中湍流参数的计算及设置：在流场的入口、出口和远场边界上，用户需要定义流场的湍流参数。在FLUENT中可以使用的湍流模型有很多种，在使用各种湍流模型时，哪些变量需要设定，哪些不需要设定以及如何给定这些变量的具体数值，都是经常困扰用户的问题。在此只讨论在边界上设置均匀湍流参数的方法，湍流参数在边界上不是均匀分布的情况可以用型函数和UDF（用户自定义函数）来定义，具体方法可参考FLUENT帮助文件。

在设置边界条件时，首先应该定性地对流动进行分析，以便边界条件的设置不违背物理规律。违背物理规律的参数设置往往导致错误的计算结果，甚至导致计算发散而无法进行下去。在FLUENT的Turbulence Specification Method（湍流定义方法）下拉列表中，可以简单地用一个常数定义湍流参数，即通过给定湍流强度、湍流黏度比、水力直径或湍流特征长度在边界条件上的值来定义流场边界上的湍流。下面具体讨论这些湍流参数的含义。

①湍流强度I（Turbulence Intensity）

式中 u′、v′、w′——速度脉动量；

u_avg——平均速度。

湍流强度小于1%时，可以认为湍流强度是比较低的，当大于10%时，则认为湍流强度是比较高的。

如果上游是没有充分发展的没有扰动的流动，则进口处可以使用低湍流强度；如果上游是充分发展的湍流，则进口处的湍流强度可以达到几个百分点。如果管道中的流动是充分发展的湍流，则湍流强度可以用式（11⁃7）计算得到，这个公式是从管流经验公式得到的。

式中D_H——Hydraulic Diameter（水力直径），作为下标是表示以水力直径为特

征长度求出的雷诺数。

液力透平出口的湍流强度通常按此公式进行估算。

②湍流的长度尺度l和水力直径。在充分发展的管流中，湍流的长度尺度l是受到管道尺寸制约的几何量，它与管道物理尺寸L的关系可以表示为

l=0.07L （11⁃8）

式中的比例因子0.07是充分发展管流中混合长度的最大值，也是管道的特征尺寸，一般是管道直径，当管道截面不是圆形时，L可以取为管道的水力直径。

湍流的特征长度取决于对湍流发展具有决定性影响的几何尺度。如果在流动中还存在其他对流动影响更大的物体，比如在管道中存在一个障碍物，而该物对湍流的发生和发展过程起着重要的干扰作用，在这种情况下，湍流特征长度就应该取为障碍物的特征长度。

因此，式（11⁃8）对于大多数管道流动是适用的，但不是普遍适用的，在某些情况下可以进行调整。在FLUENT中选择特征长度L或湍流长度尺度l的方法如下：

对于充分发展的内流，可以用Intensity and Hydraulic Diameter（湍流强度与水力直径）方法定义湍流，其中湍流特征长度就是Hydraulic Diameter（水力直径）D_H。

对于导叶下游的流场，可以用Intensity and Hydraulic Diameter（湍流强度与水力直径）方法定义湍流，并在Hydraulic Diameter（水力直径）中将导叶开口部分的长度L定义为湍流特征长度。

如果进口的流动为受到壁面限制而带有湍流边界层的流动。可以在Intensity and Length Scale面板中，用边界层厚度δ₉₉通过公式l=0.4δ₉₉，计算得到湍流长度尺度l。最后在Tur bulence Length Scale（湍流长度尺度）中输入l的值。

③湍流黏度比与湍流雷诺数Re_t成正比。

湍流雷诺数定义为

Re_t在高雷诺数边界层、剪切层和充分发展的管道流动中的数值较大，其量级大约在100～1000之间，而大多数外部流动的自由流边界层上，其值较小，通常在1～10之间。

用湍流黏度比定义流动，可以使用Tur bulence Viscosity Radio（湍流黏度比）或Intensity and Viscosity Radio（湍流强度和黏度比）进行定义。前者适用于Spalart⁃Allmaras模型，后者适用于κ⁃ε模型、κ⁃ω模型和RSM模型。

3.湍流模型

在求解雷诺数时均N⁃S方程时，需要用湍流模型封闭求解，因此湍流模型的选用成为影响内流计算精度的重要因素，但是目前还没有普遍适用的湍流模型。

在叶轮机械内部流场计算中应用较多的是零方程模型、单方程模型、双方程模型及雷诺应力模型。FLUENT提供的湍流模型包括：单方程Spalart⁃Alimaras模型、双方程模型标准κ⁃ε、重整化群RNG、可实现Realizable及雷诺应力和大涡模拟模型，如图11⁃3所示。

（1）常用的湍流模型零方程模型用代数关系式把湍流黏性系数与时均值联系起来，但只能用于射流、管流、边界层流等简单流动。

单方程模型考虑了湍动能的对流和扩散，较零方程模型合理，但必须事先给出湍流尺度的表达式，该模型主要用于边界层上。Spalars⁃Allmaras模型是单方程模型里最成功的一个模型，最早被应用于有壁面限制的流动情况中，特别在存在逆压梯度的流动区域内。该模型经常被用于流动分离区附近的计算，后来在旋转机械的计算中也得到广泛应用。FLUENT对此模型进行了改进，可在网格精度不高时使用壁面函数，通常在湍流对流场影响不大，同时网格较粗糙时，可以选用这个模型。但Spalars⁃Allmaras模型的稳定性相对较差。

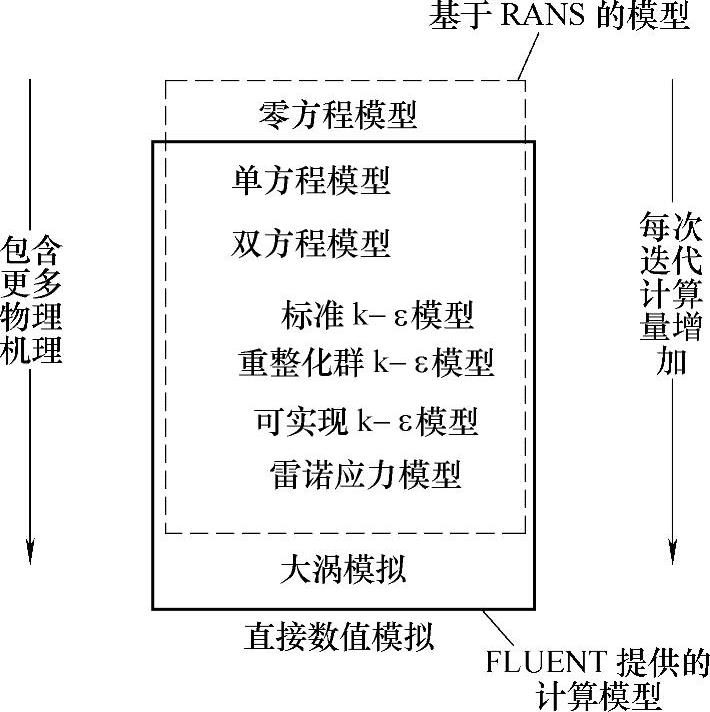
图11⁃3 湍流模型示意

标准κ⁃ε模型是最简单的双方程模型，主要是基于湍动能及其耗散率，只适合完全湍流的流动过程模拟。该模型在计算带有压力梯度的二维流动和三维边界层流动时可以取得良好的效果，但由于它采用各向同性的涡黏性假设，因而在计算旋转、曲率大、分离流动时表现得不很理想。因此近20年来，以κ⁃ε模型为基础，又提出了很多改进的方案，如重整化群模型（RNGκ⁃ε模型）和可实现模型（Realizableκ⁃ε模型）等衍生模型。这些改进后的模型也越来越广泛应用于液力透平叶轮内部流动的计算上。

RNG模型是对瞬时的N⁃S方程用重整化群的数学方法推导出来的模型。与标准κ⁃ε模型相似，它采用高Re数κ⁃ε方程，近壁处要采用壁面函数法处理，其精度较高，在流线曲率大、有漩涡和旋转的叶轮机械内部流场中更加适用。

可实现κ⁃ε模型（Realizable κ⁃ε模型）是近年才出现的，与标准κ⁃ε模型有两个主要的不同点：①该模型为湍流黏性系数给出了一个新的公式；②耗散率方程与κ⁃ε方程不同。该模型适合的流动类型比较广泛，包括有旋均匀剪切流、自由流（射流和混合层）、腔道流动和边界层流动。对以上流动过程模拟结果都比标准κ⁃ε模型的结果好，特别是可实现κ⁃ε模型在圆口射流和平板射流模拟中，能给出较好的射流扩张角。

（2）κ⁃ω模型κ⁃ω模型以湍流动能κ方程和湍流脉动频率ω方程来封闭方程组，标准模型中考虑了低Re、可压缩性、剪切流传播等因素，能够成功预测自由剪切流传播速率，像尾迹流动、混合流动、平板绕流、圆柱绕流和射流计算，以及受壁面束缚流动和自由剪切流动的计算等。

剪应力输运κ⁃ω模型（简称SSTκ⁃ω模型），综合了κ⁃ω模型在近壁区计算的优点和模型在远场计算的优点，将模型和标准κ⁃ε模型都乘以一个混合函数后再相加就得到这个模型。在近壁区，混合函数的值等于1，因此在近壁区域等价于κ⁃ω模型，在远离壁面的区域混合函数的值等于0，因此自动转换为标准κ⁃ε模型。与标准κ⁃ω模型相比，SSTκ⁃ω模型中增加了横向耗散导数项，同时在湍流黏度定义中考虑了湍流剪应力的运输过程，模型中使用的湍流常数也有所不同。这些特点使得SSTκ⁃ω模型的适用范围更广，比如可以用于带逆压梯度的流动计算、翼型计算、跨音速激波计算等。

（3）雷诺应力模型对标准κ⁃ε模型进行修正和改进：修正了ε方程的源项，并把C_μ、C₁、C₂等系数作为服从某种规律的函数；放弃了涡黏度的各向同性假设（Boussinesq假设），而是直接对6个雷诺应力分量建立输运方程并进行求解。雷诺应力模型（RSM）即为求解雷诺应力张量的各个分量的输运方程。具体形式为

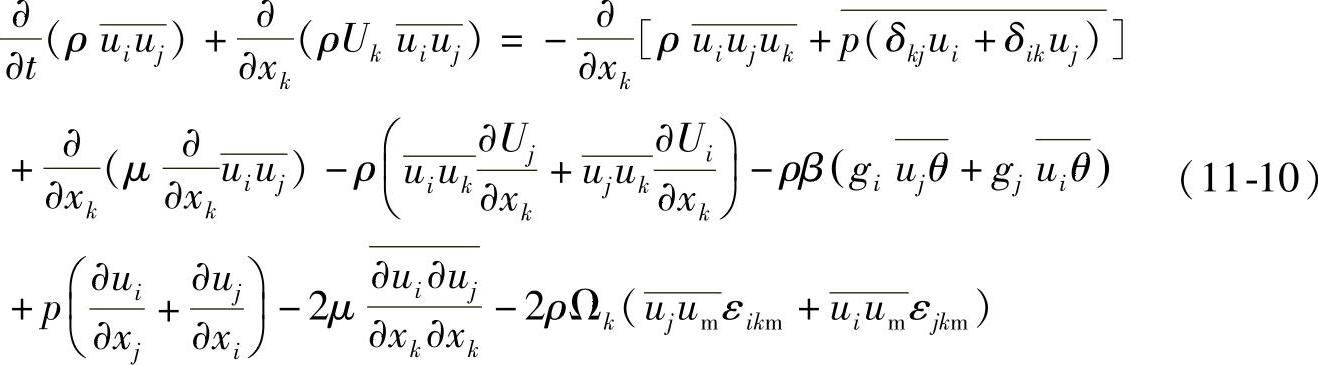
式中左边的第二项是对流项C_ij，右边第一项是湍流扩散项D_i^Tj，第二项是分子扩散项D^L_ij，第三项是应力产生项P_ij，第四项是浮力产生项G_ij，第五项是压力应变项ϕ_ij，第六项是耗散项ε_ij，第七项是系统旋转产生项F_ij。

该模型能够更好地反映湍流的物理特征，但计算量庞大，数值计算具有不稳定性，故用于进行全三维工程计算仍不普遍。只有在雷诺应力明显具有各向异性的特点时才必须使用雷诺应力模型，比如龙卷风、燃烧室内流动等带强旋转的流动问题。

（4）代数应力模型在工程实践中，对上面的雷诺应力模型方程进行进一步的简化，得到了湍流代数应力模型，简称ASM模型。其主要思路是将雷诺应力的微分方程简化为代数表达式，以减少需要求解的微分方程的个数，同时又保存湍流各向异性的特点。仍是用κ和ε的输运方程解出κ和ε，只是用代数关系计算雷诺应力。在计算量相对较小情况下，无需改进即可捕捉旋转和曲率流动的效果。因此，比较适用于离心式叶轮的内部流动，包括叶轮尾迹、叶顶间隙的数值模拟。

（5）大涡模拟湍流中包含了不同时间与长度尺度的涡旋。最大长度尺度通常为平均流动的特征长度尺度，最小尺度为Komogrov尺度。LES的基本假设是：①动量、能量、质量及其他标量主要由大涡输运；②流动的几何和边界条件决定了大涡的特性，而流动特性主要在大涡中体现；③小尺度涡旋受几何和边界条件影响较小，并且各向同性。大涡模拟（LES）过程中，直接求解大涡，小尺度涡旋模拟，从而使得网格要求比DNS低。

LES的控制方程是对N⁃S方程在波数空间或者物理空间进行过滤得到的。过滤的过程是去掉比过滤宽度或者给定物理宽度小的涡旋，从而得到大涡旋的控制方程

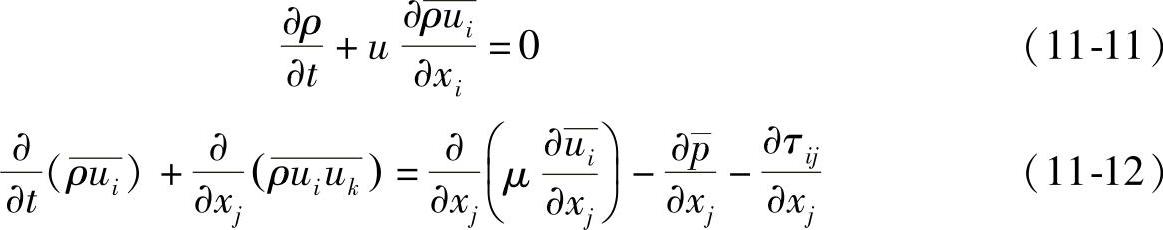
式中 τ_ij——亚网格应力，。

很明显，上述方程与雷诺平均方程很相似，只不过大涡模拟中的变量是过滤过的量，而非时间平均量，并且湍流应力也不同。

需要说明的是：计算速度的快慢与计算量成正比，即计算量大则计算速度慢，需要的时间也长。湍流模型计算中的工作量主要取决于方程的数量和方程中函数项的多少，如果不考虑大涡模拟方法，湍流模型计算从总体上说，一方程模型计算最快，双方程模型次之，雷诺应力模型最慢。

4.显示和输出结果

CFD软件通常都可以用多种方式显示和输出计算结果，如显示速度矢量图、压力等值线图、等温线图、压力云图、流线图，还可绘制XY散点图、残差图，可生成流场变化的动画，可以报告流量、力，可对界面进行面积分、体积分等，具体功能详见各软件帮助文档。

5.数值模拟结果的验证

目前大家习惯采用的对某一个数值模拟结果进行验证的方法是：采用CFD对某液力透平进行数值模拟，通过计算得到一些结果，再通过模型制作，进行试验研究，把二者进行对比，看是否一致，一致的程度越好，说明计算结果越准确，从而判定数值模拟结果的准确程度。

但这种方法并不十分科学，不能用来进行量化的比较，只能用来定性分析。因为液力透平的试验结果受到多种因素制约，例如制作因素、产品结构、试验方法和技术、试验仪器仪表精度等，而数值模拟的计算结果是对水力元件的流动状态的模拟，不能考虑所有因素的影响。实际上由于边界条件的设置、网格的划分、计算的误差、数学模型的误差等都会影响数值模拟精度，因此将两种方法得到的结果进行量化比较，并追求高度一致性的验证方法是不合理的。

为了准确评价并有效地采用CFD进行工程分析，需要针对特定的液力透平分别开展内部流场测试和CFD标准化数值试验研究，以期建立可用于液力透平CFD的准确性评估用的参考系。但这种方法的研究工作处于刚刚起步阶段，将是一项长期的任务。