液力透平优化流程及样本性能计算

本节以遗传算法作为优化算法，引入GA⁃BP神经网络作为代理模型，采用该代理模型在优化过程中替代CFD数值计算来获取优化个体中的效率和压头数据。

为了使GA⁃BP神经网络在寻优空间内有良好的目标函数响应特性，采用优化的拉丁超立方试验设计方法选择尽量多的样本点训练GA⁃BP神经网络。本书以设计变量数为5、样本数为500进行了优化的拉丁超立方试验设计，生成试验样本后，为了保证每个样本所形成的叶片是后弯型叶片，这样就要求由控制点构成的控制多边形内角小于180°或叶片型线的二阶导数恒小于0。根据这个条件，在matlab中编写相应的代码（附录），从生成的500个样本中筛选出符合上述要求的样本，得到符合要求的样本（342个）后，对每个样本点所对应的液力透平进行CFD数值计算，获得相应的性能参数。整个具体过程如下：

1）采用优化的拉丁试验设计方法生成试验样本，并筛选符合要求的试验样本。

2）根据试验样本中的控制点拟合叶片型线，为了简化该优化设计，接下来在Pro/E软件中生成等厚度叶片的叶轮，最后在Pro/E软件中生成液力透平整体模型。

3）对液力透平的模型进行网格划分。

4）采用CFD数值计算方法获取每个样本点对应的液力透平性能参数，流程如图10⁃13所示。

得到试验样本对应的液力透平水力性能参数后，即可开展GA⁃BP神经网络的学习训练，具体流程如图9⁃5所示。GA⁃BP神经网络训练完成并输出后，即可采用遗传算法开展叶片型线的性能优化，具体流程是：

1）随机生成一定规模的初始种群，从初始种群中筛选出符合后弯形叶片的样本，然后采用训练好的GA⁃BP神经网络进行目标函数的适应度评估。

2）进行遗传操作，得到新的叶片型线，并对新的叶片型线进行光顺处理。

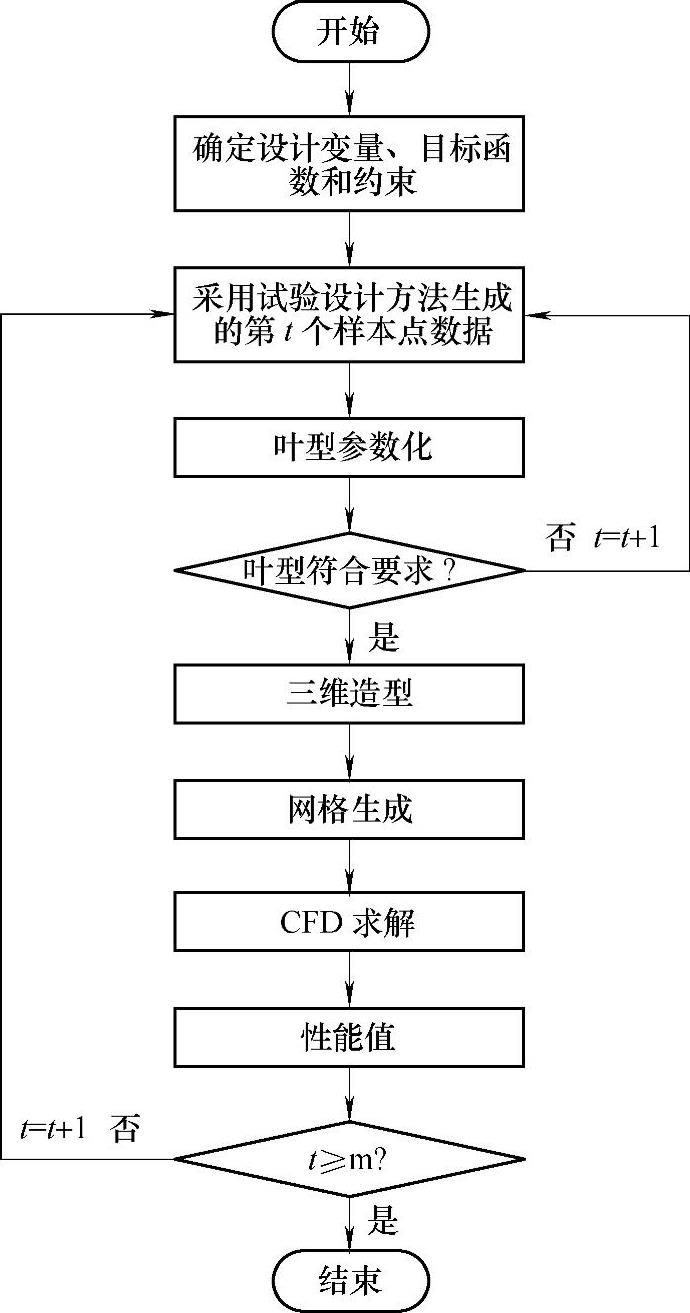
图10⁃13 试验样本性能计算流程

3）建立液力透平整体模型、划分网格和CFD数值计算。

4）进行终止条件的判断，如果满足终止条件，则结束，并输出结果，否则将得到的新个体以及其性能值一并添加到样本数据库中，再次进行GA⁃BP神经网络的学习训练，得到预测精度相对更高的GA⁃BP神经网络，重新进行上述流程，其整个优化的流程如图10⁃14所示。

图10⁃14 优化流程图

从如图10⁃14所示的优化流程中可以看出，该流程中有一个叶片型线光顺（光滑顺眼）环节，这主要是因为本节采用控制点类的B样条曲线进行叶片型线的参数化，尽管这种参数化方法解决了叶片型线曲率的不连续性问题，但是叶片型线的光顺性无法保证，而叶片型线的光顺性直接关系着叶片的质量，在一定程度上影响着叶片上的载荷分布，进而影响液力透平的能量转换能力。对于平面曲线的光顺性有四项判断准则[57]：第一，二阶几何连续；第二，曲线上没有奇点以及多余拐点；第三，曲线的曲率变化均匀；第四，应变能小，可粗略地认为曲线的绝对曲率较小。这四项判断准则中，第一项是数学上的光滑概念，仅涉及每个点及其相对充分小的范围，因此是一个局部的概念；第二项、第三项和第四项是全局的概念，其中第二项是用于控制曲线的凹凸规律，第三项控制曲线的鼓瘪变化，第四项控制曲线的整体走势。本节采用三次非均匀B样条曲线参数化叶片型线，因此叶片型线曲率连续，满足判断准则一；通过约束三次非均匀B样条曲线的控制点内角小于180°，满足本研究对叶片是后弯形叶片的要求，同时叶片型线上也不可能出现奇点和多余的拐点，符合平面曲线光顺准则二；但对于准则三和准则四就无法保证，因此要对叶片型线进行光顺处理。对于平面曲线的光顺方法有选点修改法、小波光顺和能量法等，本节对于构成叶片型线的三次B样条曲线的光顺采用应用较为广泛的曲线光顺处理方法——能量法。能量法的基本原理是：在一定的约束条件下（调整前后曲线的最大偏移量小于初始设定的值），调整样条曲线的控制点，使得样条曲线的应变能达到最小。对于一条曲线P（u），通常以式（10⁃5）表示其应变能[57]。

式中 k——曲线的曲率。

式（10⁃5）具有明确的物理意义，且可以获得较好的光顺效果，但是在进行光顺时，需要求解非线性方程组，计算量大，鉴于此，在实际应用中，通常将式（10⁃5）简化成式（10⁃6）的形式[68]。

(www.xing528.com)

式中 P（u）——样条曲线函数；

P″——函数的二次导数。

采用能量法对曲线的光顺需要确定能量函数以及优化函数的求解。下面写成两者的一般形式，将式（9⁃1）代入式（10⁃6），经过简单的推导，即可获得能量函数（见式（10⁃7））。E=dT_Nd（10⁃7）

式中 d=[d₀，d₁，d₂，…，d_n]^T——位置控制点组成的向量；

N——n+1阶的能量矩阵，其元素。

因此将样条曲线的光顺转化成如下的优化问题

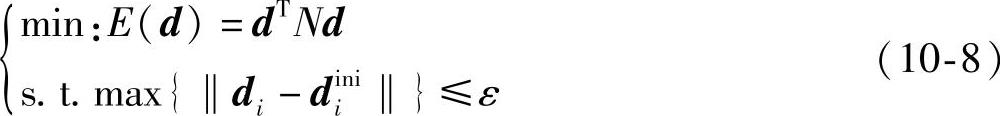
式中 d——待求的控制点向量，上标“ini”表示光顺前变量的值；

ε——设定的光顺容差。

式（10⁃8）是一个不等式约束的优化问题，为了方便优化，可以将其转化成一个无约束的优化问题，具体如下

=md^TNd+（d-dⁱⁿⁱ）TV（d-dⁱⁿⁱ）

式中 m和n_i——指定的非负常数；

V——对角元素为n_i（i=0，1，…，n）的对角矩阵。

令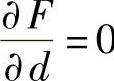，则

（V+mN）d=Vdⁱⁿⁱ （10⁃10）

求解式（10⁃10）方程组，即可获得优化问题的解。

对于叶片型线的光顺处理，理论上应该对试验设计方法生成的每个试验样本、初始种群中的每一个体以及遗传操作得到的新个体均需要做光顺处理，但这样做计算量巨大，因为这种处理不仅需要对控制点在y轴上进行调整，而且还需在x轴方向作调整，工作量大。因此，本书对每个试验样本和初始种群中的个体均先不做光顺处理，只对遗传操作得到的最优个体进行光顺处理，随后进行数值计算验证，这样就要求在叶片光顺处理过程中控制点的调整不能过大，一方面是尽可能小的偏离优化得到的叶型，另一方面是如果光顺前后叶型变化小，其水力性能变化相对较小，这样就减小了试验样本和初始种群中的个体没有经过光顺处理引起的误差。