【摘要】:对于液力透平叶片型线开展流体动力学优化的目的是使其在最优工况附近具有更好的性能,从而提高其能量转换能力。方程右边第1项的目的是极大化液力透平在三个指定工况点下的水力效率,第2项是为了消除液力透平在三个指定工况下效率过大的差别,该项展开式如式所示;第3项为惩罚项,对不满足压头约束的情况进行惩罚。
对于液力透平叶片型线开展流体动力学优化的目的是使其在最优工况附近(25m3/h,27.5m3/h,30m3/h)具有更好的性能,从而提高其能量转换能力。本节以图10⁃12所示的控制点②、③、④、⑤和⑥的坐标(x,y)为设计变量,为了减少设计变量的个数,使各个设计的自由度均为1,即所选控制点只在xy平面内的一个方向上进行变化。具体是控制点③、④、⑤沿y轴方向上下变化,即变量用(y3,y4,y5)表示;另外,在研究过程中为了保持叶片进、出口角以及叶片进、出口位置不变,控制点②、⑥在叶片进、出口端点处的切线方向上变化,变量计为y2和y6,其中x2和x6可根据叶片进、出口端点处的切线方程求出;控制点①、⑦坐标保持不变。为了获得设计变量尽可能大的搜寻空间,本研究最终确定设计变量的取值范围见表10⁃7。
表10⁃7 设计变量的变化范围

在优化过程中,为了使液力透平的压头不发生大的变化,约束3个流量下的压头变化范围均在初始设定的范围之内,本次液力透平叶片型线优化的最终目标函数可表述如下
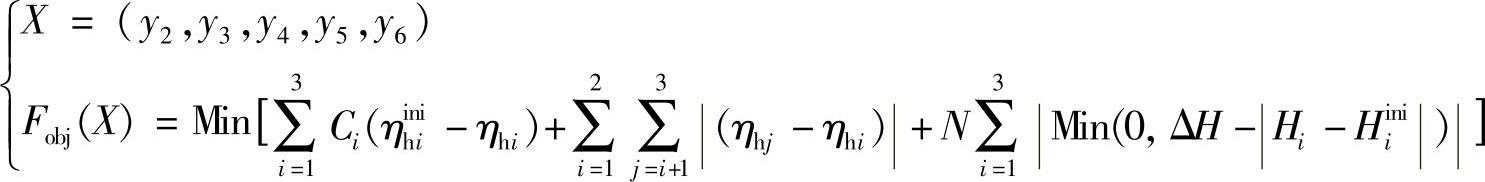
(10⁃3)
式中 Fobj(X)——优化设计的目标函数;X——设计变量;
i=1,2,3——在优化过程中指定的三个工况点;(https://www.xing528.com)
Ci——权重系数;
ηh——液力透平的水力效率;
H——液力透平的压头;
N——罚因子;
上标ini——初始叶片型线对应的液力透平的性能参数。
方程(10⁃3)右边第1项的目的是极大化液力透平在三个指定工况点下的水力效率,第2项是为了消除液力透平在三个指定工况下效率过大的差别,该项展开式如式(10⁃4)所示;第3项为惩罚项,对不满足压头约束的情况进行惩罚。
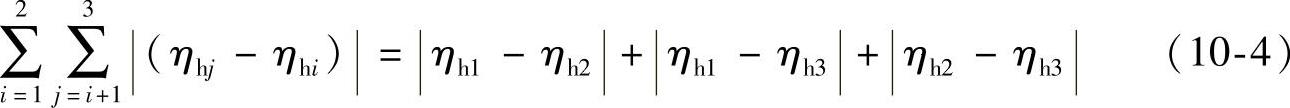
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




