优化前后叶轮轴面图的几何对比

1.优化前后叶轮轴面图的几何对比

根据上述优化流程，对本书所研究液力透平的叶轮轴面投影图进行优化，优化时遗传算法参数设置如下：种群规模为60，进化代数为40，交叉概率设定为0.8，变异概率设为0.2。优化前后设计变量对比见表10⁃2。

表10⁃2 优化前后叶轮轴面投影图的参数对比

优化前后液力透平叶轮轴面投影图的几何形状对比如图10⁃5所示。

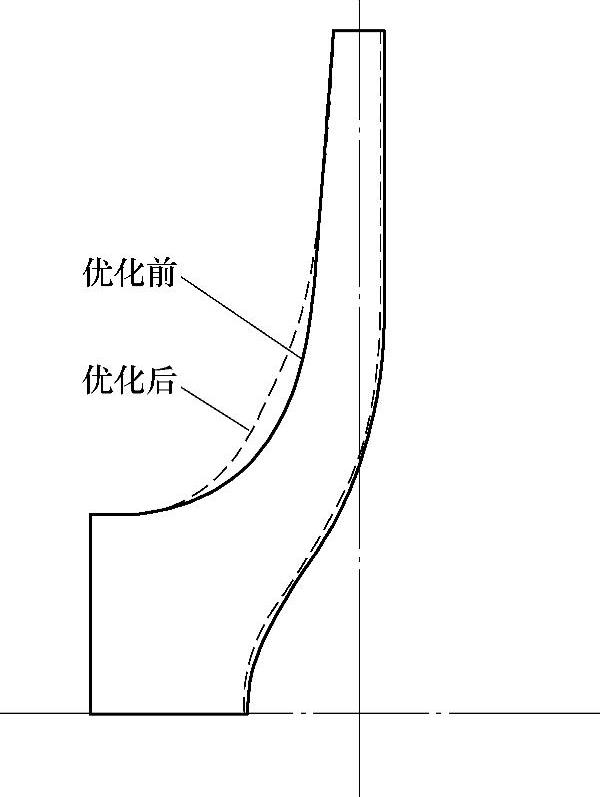
图10⁃5 优化前后叶轮轴面投影图的几何比较

2.叶轮轴面图优化前后液力透平外特性对比

为了比较优化前后叶轮轴面投影图的性能差异，采用CFD数值计算的方法对优化前后的液力透平模型分别进行了数值计算。优化前后液力透平在最优工况下的效率与压头值见表10⁃3。

表10⁃3 优化前后初始模型与优化后模型的性能对比

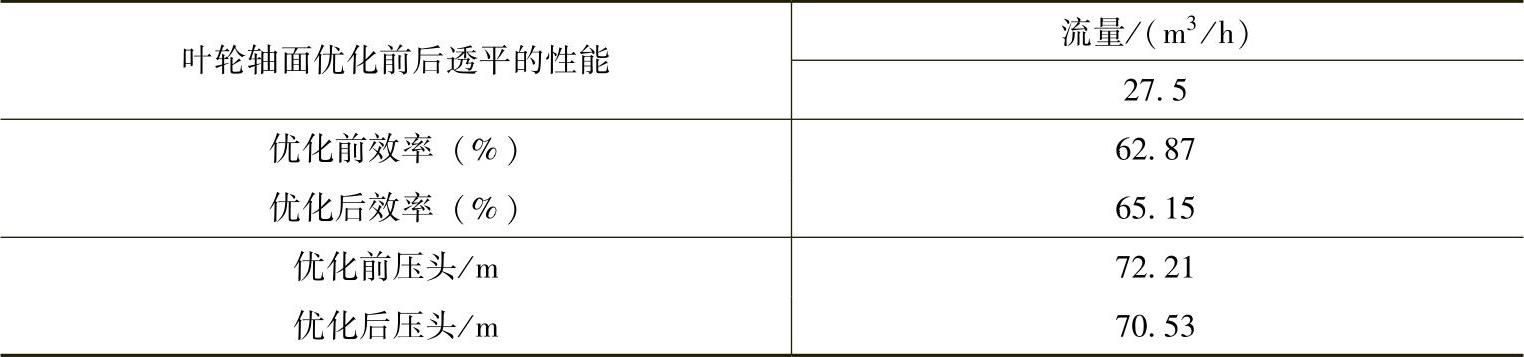
从表10⁃3中可以看出，优化后的模型在最优工况下的效率比初始模型的效率提高了2.28%，且压头在初始设定的范围之内。

为了进一步研究优化后其他工况下液力透平的性能，除优化时的1个工况（最优工况）外又增设了8个工况点对其进行了CFD数值计算，外特性结果如图10⁃6所示。

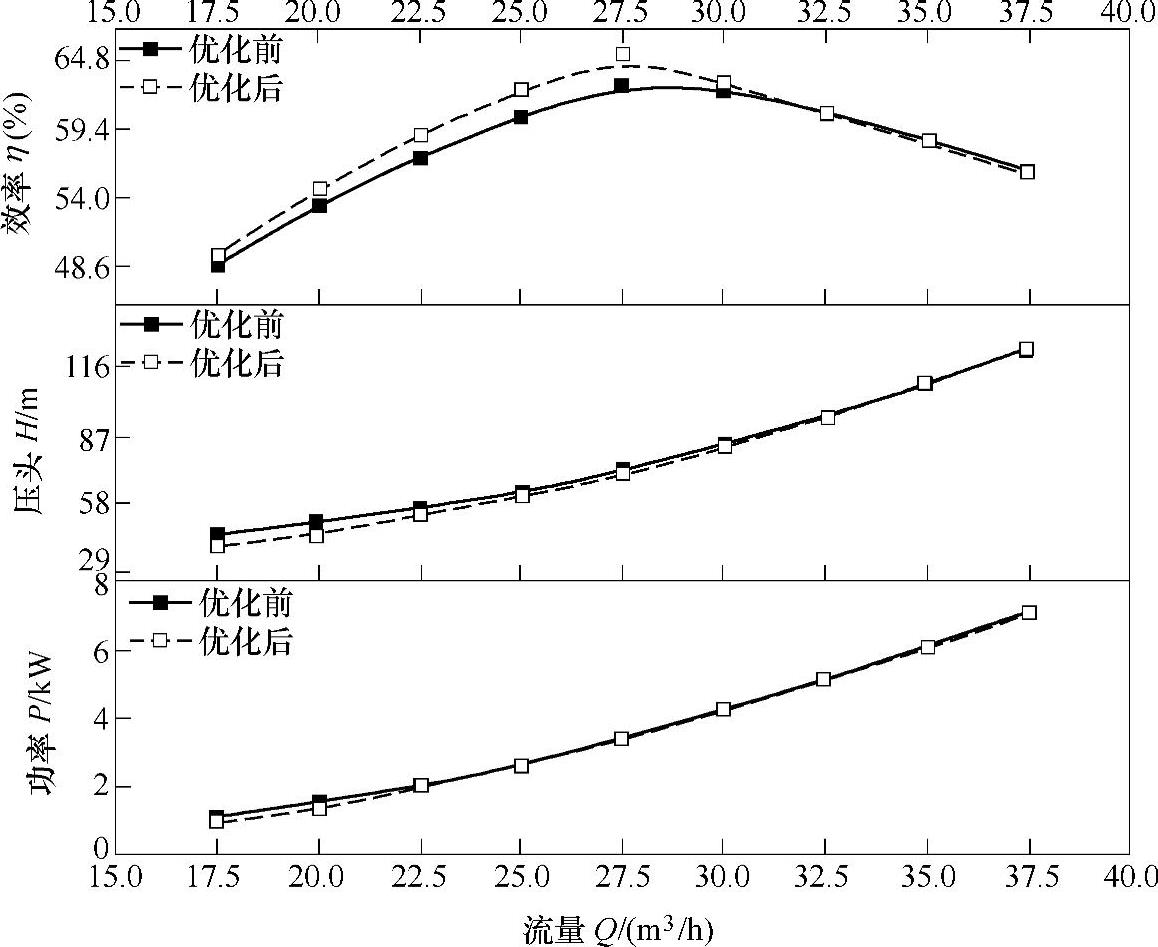
图10⁃6 优化前后液力透平的外特性曲线(www.xing528.com)

从图10⁃6可以看出，优化后的液力透平除了在指定工况点（最优工况）的效率有所提升外，在小流量工况及部分大流量工况下效率均有所提升，只是随着流量的进一步增大，优化后液力透平的效率与优化前的效率相当。这主要是因为本节的优化只是针对最优工况点进行的，优化后液力透平在最优工况点效率得到了提升，说明第9章建立的优化方法的有效性，但存在其他工况效率下降的可能性。因此为了使得优化后的液力透平在较大范围内性能均有所提升，在计算量允许的情况下，应该在多个工况点下对叶轮轴面图进行优化。

3.优化前后叶轮轴面的内流场对比分析

如图10⁃6所示为液力透平优化前后的外特性曲线，外特性是内特性的外在表现，为此应该对优化前后的内特性加以分析，以明确优化前后液力透平外特性变化的内在原因，可为液力透平叶轮的进一步优化提供参考。

如图10⁃7所示为优化前后液力透平分别在一个小流量工况（22.5m³/h）、最优工况（27.5m³/h）和一个大流量工况（32.5m³/h）下叶轮轴截面上的湍流耗散率分布。湍流耗散率[67]是流体分子在黏性作用下由湍流动能转化成分子热运动动能的速率，其值越大表明单位质量流体在单位时间内损耗的湍流动能越多，即损失越大。

图10⁃7 不同流量下叶轮轴截面上的湍流耗散率云图

a）22.5m³/h b）27.5m³/h c）32.5m³/h （彩图见书后插页）

从图10⁃7可以看出，小流量工况下叶轮中的湍流耗散率在叶轮出口区域相对较大，其他地方相对较小，而大流量工况下整个流道中的湍流耗散率均相对比较大，其中最大处在叶轮叶片的出口区域。另外，从图中也可以看出，在小流量工况和最优工况下，优化后叶轮中的湍流耗散率要明显小于优化前叶轮中的湍流耗散率，特别是在最优工况下。而在大流量工况下，优化后叶轮中的湍流耗散率要大于优化前叶轮中的湍流耗散率，这与图10⁃6中大流量工况下优化后液力透平的效率略低于优化前液力透平的效率相符。

图10⁃7从湍流耗散率的角度分析了液力透平在不同流量下叶轮中的流动特点，在小流量工况和最优工况下，优化后叶轮中湍流耗散率小于优化前湍流耗散率。但叶轮中湍流耗散损失是湍流耗散率对体积的积分[见式（10⁃2）]，从叶轮轴面投影图优化前后的几何对比（图10⁃5）中可以看出，优化后叶轮流体域的体积要大于优化前的体积，因此在小流量工况和最优工况下优化前后叶轮中的湍流耗散损失需要通过式（10⁃2）计算求得，并进行对比（图10⁃8）。从图10⁃8中可以看出，在小流量工况和最优工况下，优化后叶轮中的湍流耗散损失小于优化前叶轮中的湍流耗散损失；而大流量工况下优化后的湍流耗散损失则大于优化前的湍流耗散损失。

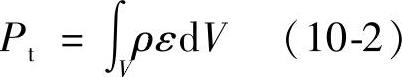
式中 P_t——湍流耗散的功率；

ε——湍流耗散率。

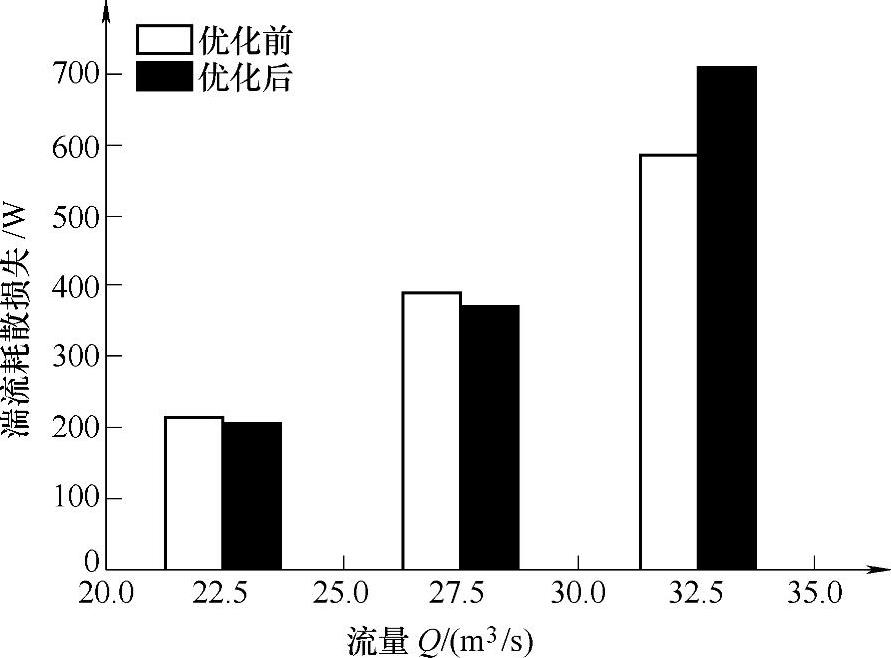
图10⁃8 不同流量下叶轮中湍流耗散损失分布