遗传算法的基本原理解析

遗传算法是根据所解决问题的目标函数来构造适应度函数（Fitness Function），对问题可能潜在解集的种群（Population）进行评估、遗传操作、选择，按照适者生存和优胜劣汰的原理逐代（Generation）繁殖进化，最后获得适应度值最好的个体（individual）作为所解决问题的最优解。其具体操作实现流程如下：

1.遗传编码

遗传算法不能直接处理问题的空间变量，需要将参数转换成按一定结构组成的个体或染色体，即从变量的表现型到基因型的映射，这个映射操作称之为编码。通常遗传算法有两种编码方法：一种是二进制编码，它是将变量值代表的个体表示成一个{0，1}二进制串，串长短取决于求解的精度要求；另外一种是实数编码，它是采用十进制的实数对变量值进行编码，编码串的长度与优化问题所含的变量个数相等。

2.初始种群的设定

初始种群是随机生成，它的产生方式依赖于步骤（1）中的编码方式。对于初始种群的设定问题就是确定种群规模的大小，即种群中所含个体数目多少。个体数目的多少会在一定程度上对遗传算法效能的发挥产生一定的影响的。个体数目少，遗传算法的计算速度相对较高，但是种群缺乏多样性，优化后得到的结果一般不会很好。随着个体数目增多，种群多样性得到提高，算法陷入局部收敛的可能性降低，生成有价值的基因并逐步进化，最后得到全局最优解的概率增大。但是，如果个体数目太多，这也就相应地增加了遗传算法的计算量，使得收敛时间增长，计算效率下降。因此，群规模的大小需要根据计算机的硬件能力和计算的复杂度确定。

3.适应度函数选取及计算

遗传算法在进化过程中基本不需要其他外部信息，仅需要适应度函数，适应度函数是用于评估个体适应度优劣的函数。适应度越高，遗传到下一代的可能性就越大，反之，适应度越低，遗传到下一代的可能性就会相对较小。因此适应度函数的确定是比较重要的，一般来说，适应度函数是通过问题的目标函数转化而成的。常见的适应度函数有三种[64]：

（1）直接将目标函数转化成适应度函数，即：

如果目标函数为最大化问题，则Fit（f（x））=f（x）（9⁃6）

如果目标函数为最小化问题，则Fit（f（x））=-f（x）（9⁃7）

（2）如果目标函数是最小化问题，则

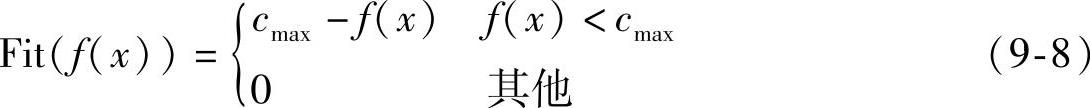
如果目标函数是最大化问题，则

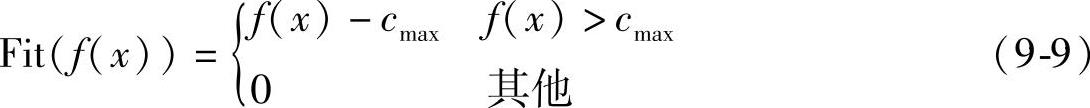
式中 c_max——f（x）的最大值估计。

（3）如果目标函数是最小化问题，则

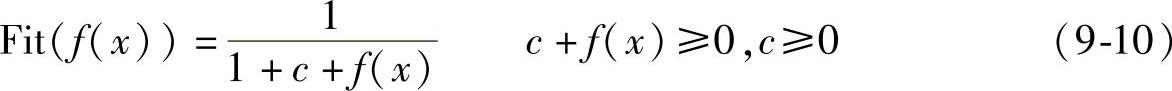(www.xing528.com)

如果目标函数是最大化问题，则

基于适应度函数在进行选择操作时可能会出现种群的早熟（提前收敛）或者对重点区域无法进行搜索的现象，为了避免上述问题的产生，需要对个体的适应度函数进行适当地调整，比如为了提高个体的竞争能力，可以扩大最佳个体的适应度和其他个体的适应度的差异程度，这种适应度调整称之为适应度函数的尺度变换。常用的个体适应度变换方式有三种：线性变换、幂函数变换和指数变换。

4.遗传操作

遗传操作包含选择算子、交叉算子和变异算子，这三个算子是遗传算法的精髓，利用这些算子产生新一代的种群，从而实现种群的进化过程。

选择操作是以概率的形式对个体进行选择，其中个体概率的大小取决于种群中个体的适应度值及其分布。常用的选择方法有：轮盘赌选择法（Roulette Wheel Selection）、随机变量抽样法（Stochastic Universal Sampling）、局部选择法（Local Selection）、锦标赛选择法（Tournament Selection）等，在这些选择方法中，轮盘赌选择法相对操作简单，容易理解，并且理论相对成熟，因此本书中选择轮盘赌选择法作为遗传算法的选择机制。

交叉运算是指将两个个体的部分结构以某种方式进行交换，形成新个体的操作。交叉是遗传算法中获得新优良个体最重要的操作。遗传算法中交叉算子有：单点交叉、双点交叉、多点交叉、均匀交叉、循环交叉等，其中使用最多的是单点交叉与双点交叉。本书中的交叉操作采用的是单点交叉。

变异是指将交叉之后的子个体变量以很小的概率或者步长发生改变，对于{0，1}编码而言，就是在基因某个位置反转其位值。变异操作同样是遗传算法中的主要算子，其本身是一种局部随机搜索，它与选择算子、交叉算子相结合，有力地确保了遗传算法的有效性，使得遗传算法具有局部搜索能力，同时使遗传算法保持了种群的多样性，以防出现早熟收敛。

5.终止条件的判断

遗传算法中判断终止条件的方法有：适值边界方法、时间边界方法和进化代数方法。基于本书中无法给出确切的终止时间以及确切的优化精度，而可以给出进化代数，因此本书以进化代数作为判断算法是否终止的条件，即进化代数方法。

6.判定是否终止

如果满足所设定的终止条件，则终止，否则转到步骤3继续进行个体的适应度评估以及对种群的遗传操作。

如图9⁃6所示为遗传算法的优化流程图。

图9⁃6 遗传算法优化流程图

采用遗传算法对液力透平的几何参数进行优化时，其水力性能的CFD数值计算无疑是非常耗时的，因此本书还需引入代理模型来代替在寻优过程中获取液力透平性能参数的CFD数值计算，这样便可节省计算成本，缩短优化时间。下面对代理模型加以介绍。