代理模型的近似方法及遗传算法优化BP神经网络

代理模型的实质是采用近似方法对离散的数据加以拟合而建立的一种数学模型。目前，在优化设计中使用较多的代理模型近似方法有：多项式响应面模型、Kriging模型、径向基函数模型和BP神经网络模型等。下面对BP神经网络模型作详细的介绍。

BP神经网络模型及优化的BP神经网络

人工神经网络（Artificial Neural Network，ANN），又称连接主义模式，是模仿人脑的结构与特性，通过大量基本处理单元（神经元）按照某种拓扑结构连接而形成的一种新型信息处理和非线性动力系统。它具有高度非线性映射能力、很强的自适应学习能力、并行性、结构可变性、鲁棒性和容错能力等特点。因此，它在很多研究领域己经得到了广泛的应用。从人工神经网络的实际应用中（如函数的逼近、数据的压缩、模式识别和分类、滤波等）发现，接近90%的人工神经网络采用的是反向误差传播神经网络（Bac kPropagation Neural Network，BP）或者是它的衍生形式，它同时也是前馈型神经网络的核心部分。下面对BP神经网络及其基本数学原理进行介绍。

Rumelhart和McCelland等人于1986年在书中对BP神经网络作了详尽的描述与分析[62]。神经网络最基本的结构是由输入层、隐含层（中间层）和输出层三层结构组合而成，如图9⁃3所示，其中输入节点数目为n，输出节点数k，ω_a、ω_b分别为输入层和隐含层与隐含层和输出层之间的连接权值。

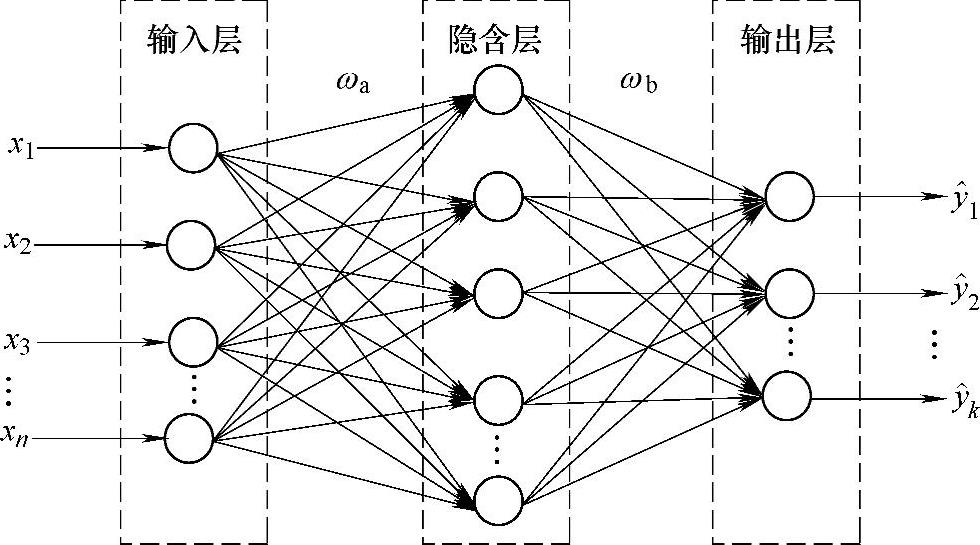
图9⁃3 三层BP神经网络结构

BP神经网络学习训练的基本思想是在给定输入信息和输出信息的情况下，对网络的权值和阈值进行不断的修正，使得网络能够实现该给定的输入输出的映射关系。具体实施过程如图9⁃4所示：首先，输入样本信息，从输入层传入，经隐含层逐层处理，一直传到输出层；其次，对输出层的实际输出值与期望值进行对比，如果输出值与期望值的误差在可接受的范围内，则停止训练，反之，需要将误差信息以某种形式经隐含层向输入层逐层反向传播，并将误差信号分摊给每层中的所有单元，以分摊后的误差信号分别作为修正各个单元权值的依据，这种正向传播与反向传播一直进行着，直到输出值与期望值的误差在可接受的范围内，则停止训练；最后，输出训练好的BP网络。(www.xing528.com)

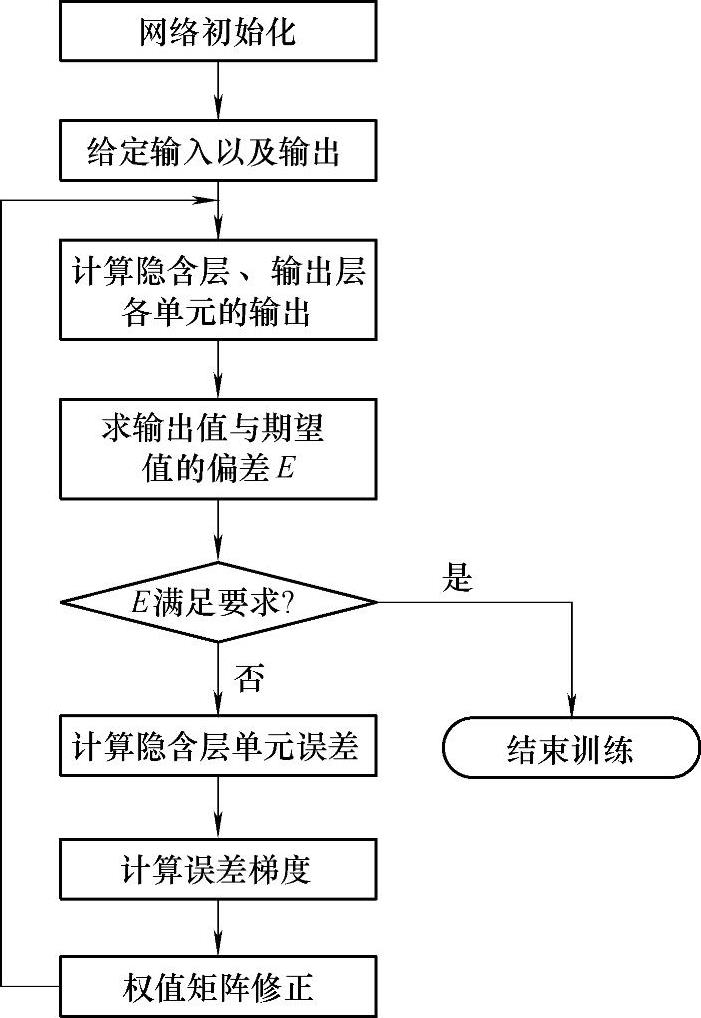
图9⁃4 BP神经网络流程图

BP神经网络结构确定后，对于初始权值和阈值而言，它们是随机生成的，但初始权值和阈值对网络的收敛速度及预测精度有很大的影响而又无法准确获得。针对于此，可以采用遗传算法以预测的误差最小为目的，初始权值和阈值为设计变量，找出最优的权值和阈值，以寻找得到的最优权值和阈值作为BP神经网络的权值和阈值，这样不仅使得网络训练有较快的收敛速度，而且有更好的预测精度。本书后续章节的优化过程中所采用的神经网络即为用遗传算法优化的BP神经网络（GA⁃BP）。如图9⁃5所示为采用遗传算法优化BP神经网络的流程图。

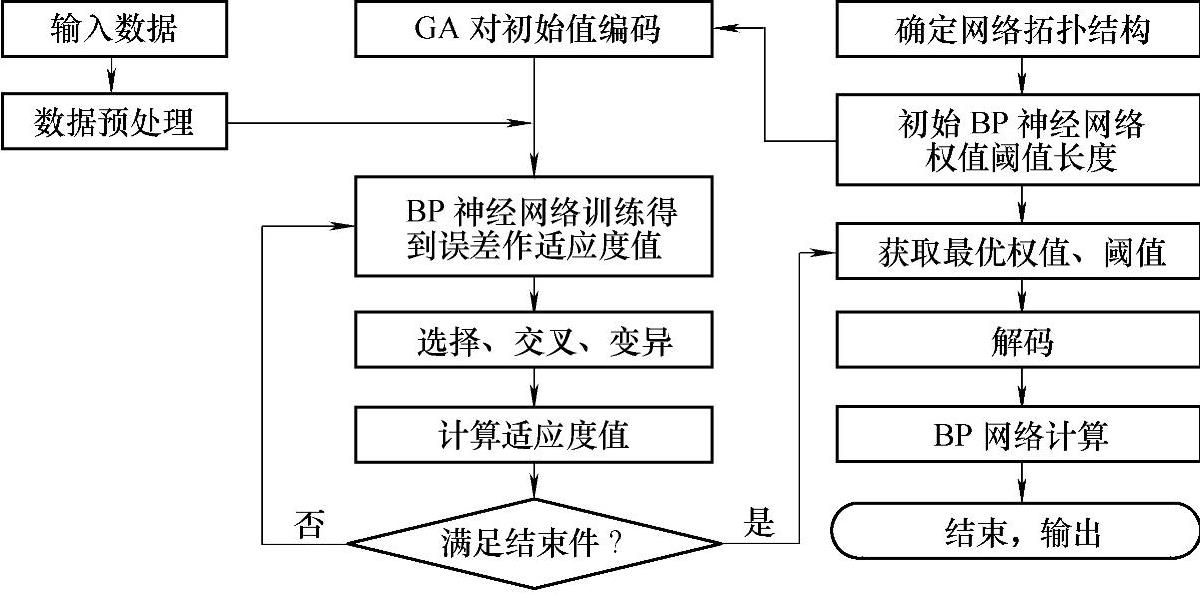
图9⁃5 遗传算法优化BP神经网络的流程