蜗壳内压力脉动分析

1.蜗壳内周向压力脉动分析

如图6⁃13所示为蜗壳内周向各监测点处在两个周期内的压力脉动时域图。从图6⁃13可以看出添加导叶后蜗壳内周向压力减小，且周向各监测点处之间的压力脉动幅值差值也减小。还可以看出当导叶数等于7时蜗壳周向各监测点处之间的压力脉动程度基本相同，而随着导叶数的增加监测点6处的压力脉动程度与其他监测点处之间的压力脉动程度的差值逐渐增加。

如图6⁃14所示为通过快速傅里叶变换得到的蜗壳内周向各监测点处压力脉动的频域图。

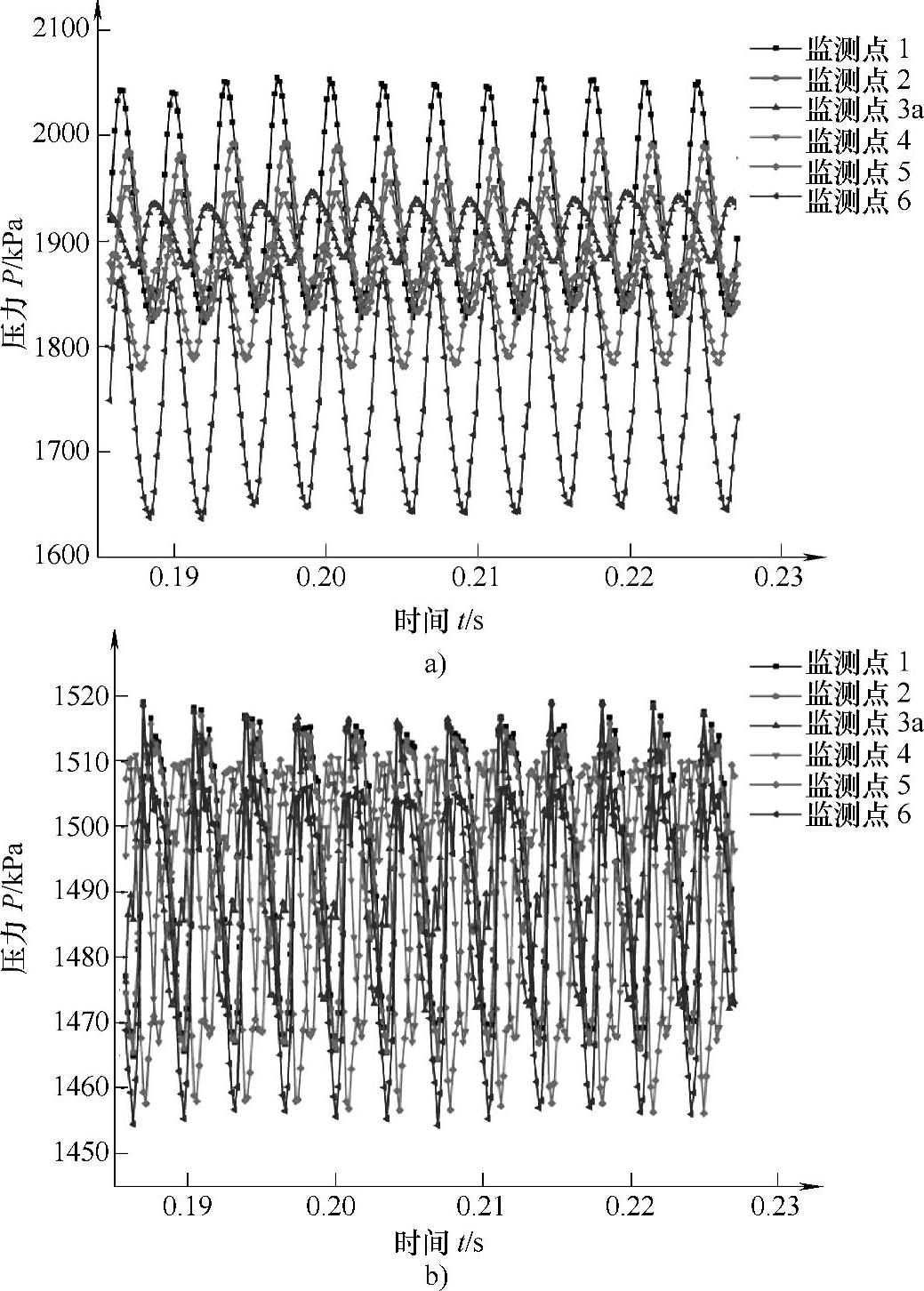
图6⁃13 蜗壳内周向压力脉动时域图

a）导叶数z=0 b）导叶数z=7 （彩图见书后插页）

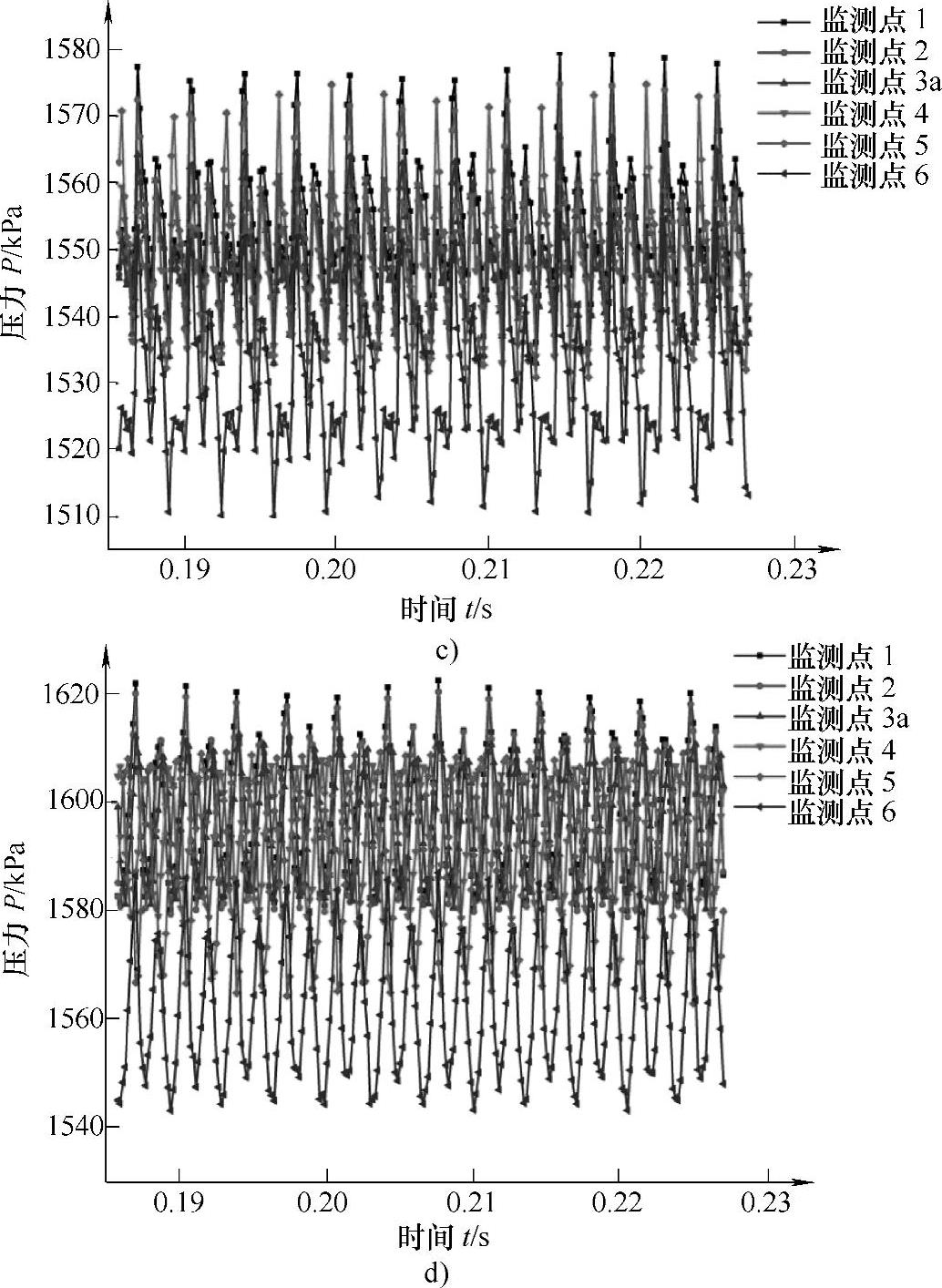
图6⁃13 蜗壳内周向压力脉动时域图（续）

c）导叶数z=9 d）导叶数z=11 （彩图见书后插页）

蜗壳内周向各监测点处的压力脉动的主频幅值和最大脉动幅值见表6⁃1。

表6⁃1 蜗壳内周向压力脉动的主频幅值和最大脉动幅值

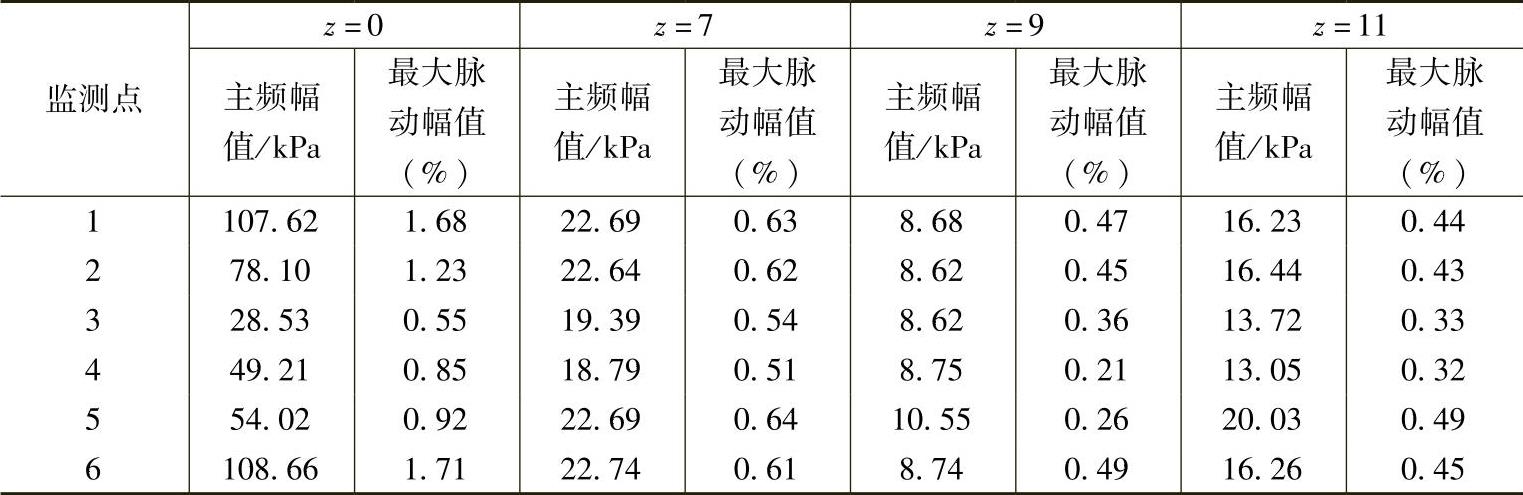
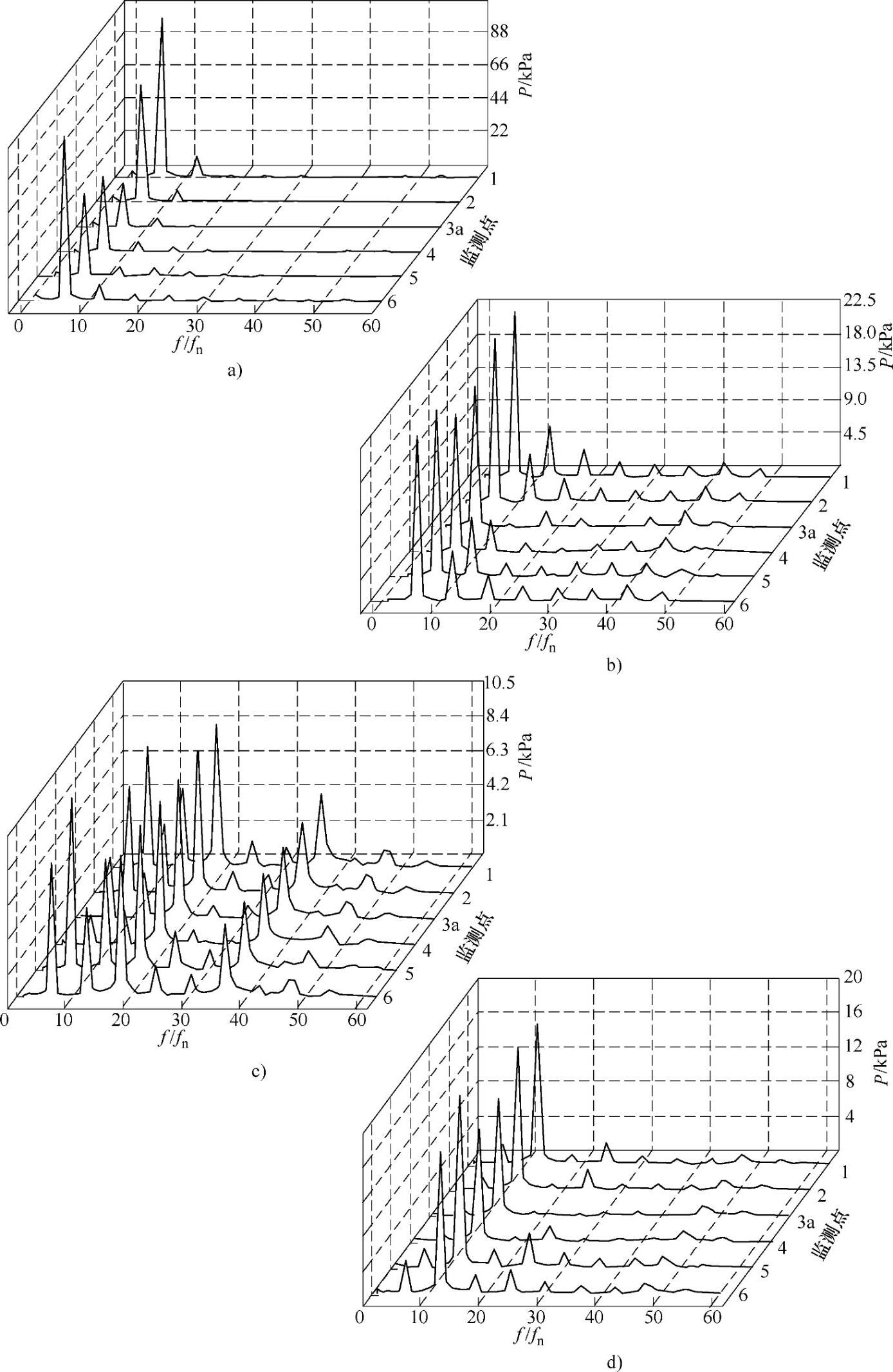
图6⁃14 蜗壳内周向压力脉动频域图

a）导叶数z=0 b）导叶数z=7 c）导叶数z=9 d）导叶数z=11

结合图6⁃14和表6⁃1可以看出在未加导叶时蜗壳内周向各监测点处越接近隔舌位置其压力脉动的主频幅值和最大脉动幅值越大，而添加导叶后蜗壳内周向各监测点处的压力脉动主频幅值和最大脉动幅值均相应减小，且周向各处的压力脉动主频幅值和最大脉动幅值彼此之间相对于添加导叶之前非常接近。这主要是因为添加导叶后蜗壳内各监测点距离叶轮进口较远，受到叶轮动静相互干涉作用的影响也就较小。结合图6⁃3也可以看出未加导叶时叶轮进口有明显的尾迹效应，且叶轮进口的叶片背面产生了与叶轮旋转方向相同的漩涡，而添加导叶后叶轮进口无漩涡产生，叶轮内液流流动较为均匀。由于尾迹效应是产生动静相互干涉的主要原因之一，又压力脉动是叶轮动静相互干涉、涡流和回流等诸多因素相互作用的外在动态反映，所以这些因素导致添加导叶后蜗壳内周向各监测点处的压力脉动主频幅值和最大脉动幅值降低。

由表6⁃1还可以看出，当导叶数等于7时蜗壳内周向的最大压力脉动主频幅值和最大脉动幅值分别为未加导叶时的最大压力脉动主频幅值和最大脉动幅值的0.21倍和0.37倍；当导叶数等于9时蜗壳内周向的最大压力脉动主频幅值和最大脉动幅值分别为未加导叶时的最大压力脉动主频幅值和最大脉动幅值的0.10倍和0.29倍；当导叶数等于11时蜗壳内周向的最大压力脉动主频幅值和最大脉动幅值分别为未加导叶时的最大压力脉动主频幅值和最大脉动幅值的0.18倍和0.29倍。可见，叶轮进口前添加导叶可以有效降低蜗壳内周向最大压力脉动幅值。

由图6⁃14和表6⁃1还可以看出当导叶数等于9时蜗壳内周向各监测点处的压力脉动主频幅值最小，其次为导叶数等于11，而导叶数等于7时最大，这是因为由图6⁃3可知导叶数越少叶轮进口的尾迹效应越显著，即叶轮动静相互干涉作用越强，因此蜗壳内周向各监测点处的压力脉动受到叶轮动静相互干涉作用的影响就越大。由图6⁃3还可以看出当导叶数等于9时蜗壳内周向各监测点处的速度最小，导叶数等于11时最大，因此当导叶数等于9时蜗壳内周向各监测点处的压力脉动主频幅值最小。还可看出随着导叶数的增加，蜗壳内周向各监测点处的最大脉动幅值逐渐减小。这是因为由上述研究结果可知随着导叶数的增加，液力透平的水头逐渐增加，而蜗壳内最大压力和最小压力的差值变化较小，所以蜗壳内周向各监测点处的最大脉动幅值逐渐减小。

由表6⁃1还可以看出当导叶数等于7和11时距离蜗壳隔舌附近的监测点处的压力脉动主频幅值较大，而当导叶数等于9时蜗壳周向各监测点处的压力脉动主频幅值相差较小，这是因为由图6⁃3可知导叶数越少越易受到叶轮动静相互干涉作用的影响，且隔舌处速度变化较大，所以当导叶数等于7时隔舌附近的监测点处的压力脉动主频幅值较大，而随着导叶数的增加导叶内的过流面积逐渐减小，导叶进口速度逐渐增加，隔舌附近的速度变化也逐渐增大，所以当导叶数等于11时隔舌附近的监测点处的压力脉动主频幅值较大。因此当导叶数等于9时蜗壳内周向各监测点处的压力脉动主频幅值相差较小。可见，当导叶数等于9时蜗壳内周向各监测点处的压力脉动主频幅值最小。

2.蜗壳内径向压力脉动分析

如图6⁃15所示为通过快速傅里叶变换得到的最优工况下蜗壳内径向各监测点处压力脉动的频域图。蜗壳内径向各监测点处的压力脉动主频幅值和最大脉动幅值见表6⁃2。结合图6⁃15和表6⁃2可以看出未加导叶时蜗壳径向各监测点处的压力脉动主频幅值和最大脉动幅值随着距离叶轮进口越近增加程度相对添加导叶后较大，这主要是因为由图6⁃3可知未加导叶时蜗壳径向速度变化较大，且距离叶轮进口越近，受到叶轮动静相互干涉作用的影响就越大。因此添加导叶后蜗壳径向压力脉动主频幅值和最大脉动幅值随着距离叶轮进口越近其增加程度相对越小。

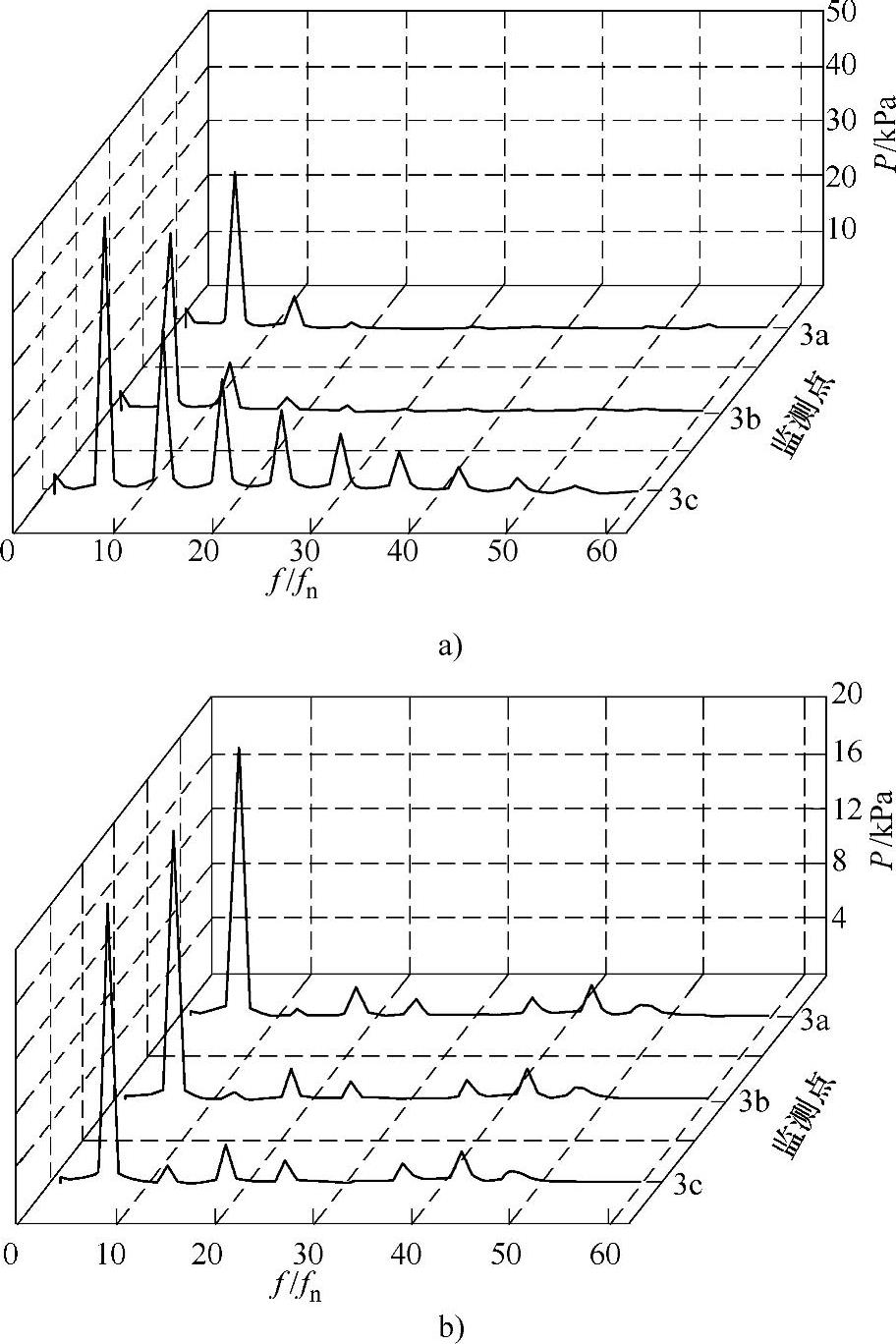
图6⁃15 蜗壳径向压力脉动频域图

a）导叶数z=0 b）导叶数z=7

(www.xing528.com)

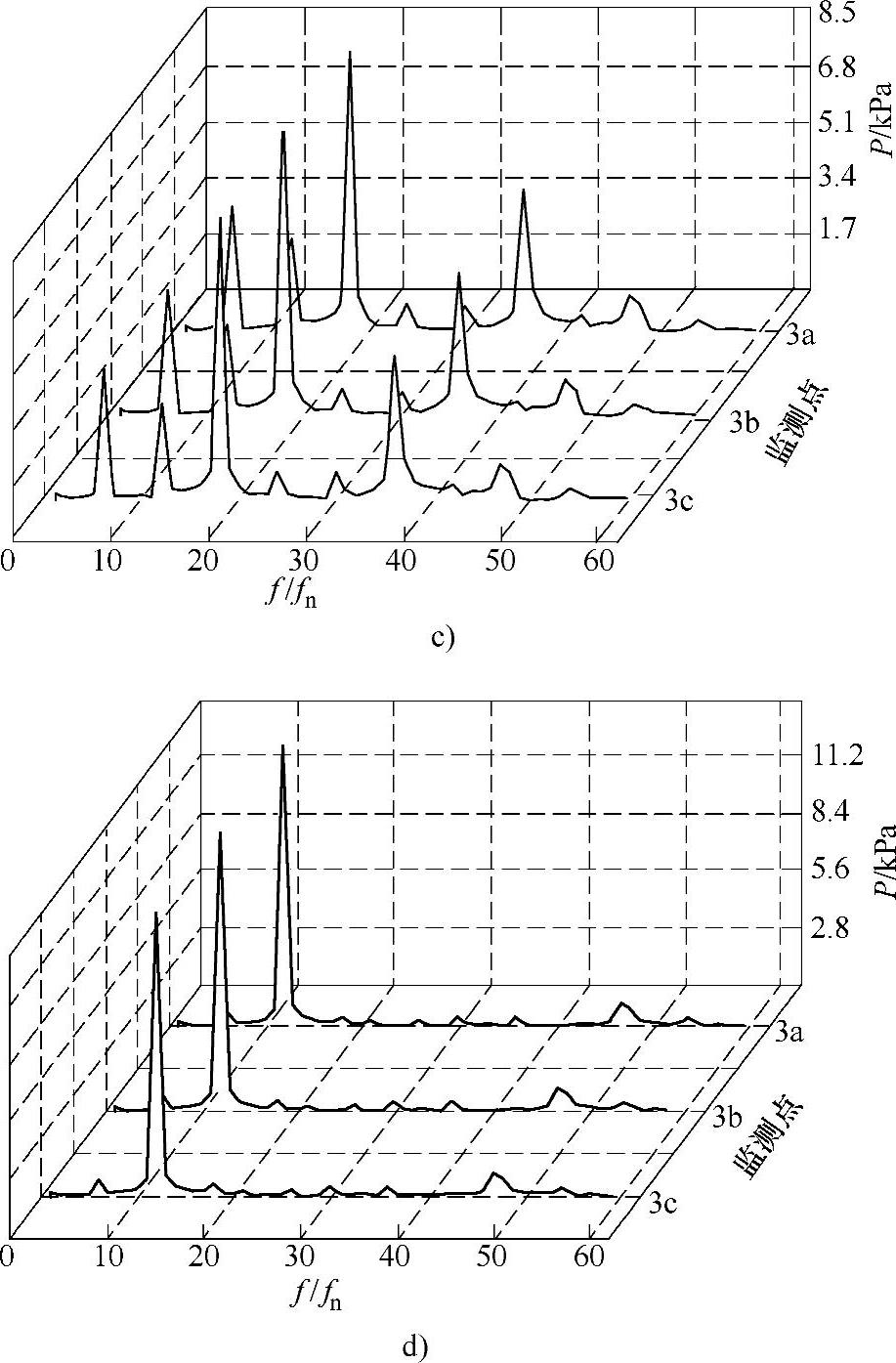
图6⁃15 蜗壳径向压力脉动频域图（续）

c）导叶数z=9 d）导叶数z=11

表6⁃2 蜗壳内径向压力脉动的主频幅值和最大脉动幅值

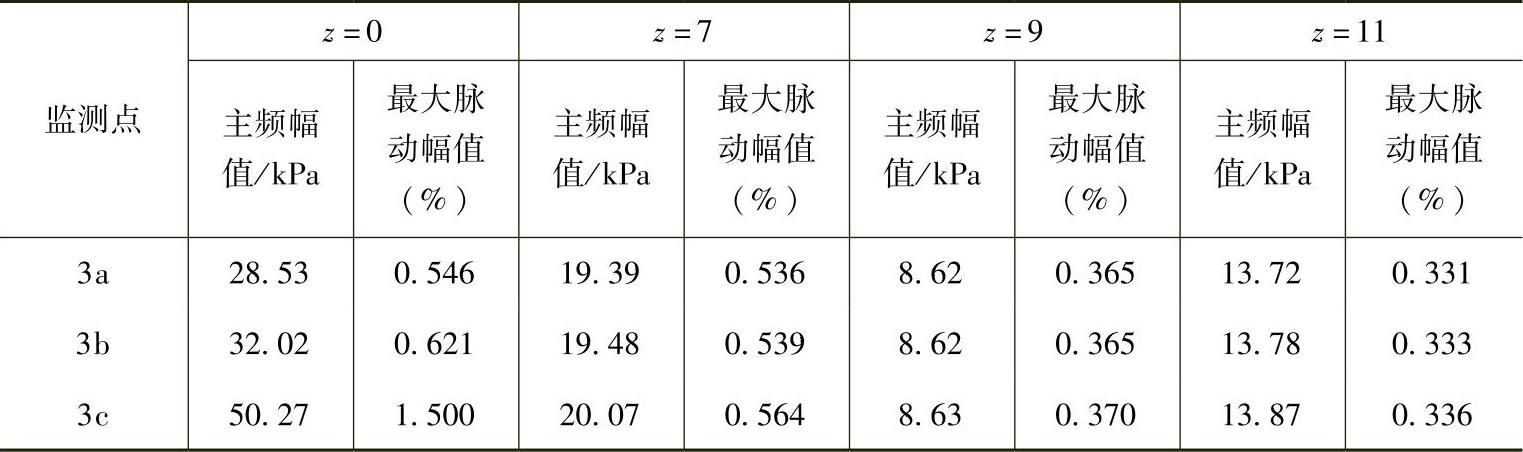
由图6⁃15和表6⁃2可以看出添加导叶后蜗壳径向压力脉动主频幅值和最大脉动幅值均相应减小，且当导叶数等于7时蜗壳内径向的最大压力脉动主频幅值和最大脉动幅值分别为未加导叶时的最大压力脉动主频幅值和最大脉动幅值的0.40倍和0.38倍；当导叶数等于9时蜗壳内径向的最大压力脉动主频幅值和最大脉动幅值分别为未加导叶时的最大压力脉动主频幅值和最大脉动幅值的0.17倍和0.25倍；当导叶数等于11时蜗壳内径向的最大压力脉动主频幅值和最大脉动幅值分别为未加导叶时的最大压力脉动主频幅值和最大脉动幅值的0.28倍和0.22倍。可见，叶轮进口前添加导叶也可以有效降低蜗壳内径向最大压力脉动幅值。

由图6⁃15和表6⁃2还可以看出在不同导叶数下蜗壳内径向各监测点距离叶轮进口越近，这些位置处的压力脉动主频幅值和最大脉动幅值越大。这是因为距离叶轮进口越近受到叶轮动静相互干涉作用的影响越大，所以这些位置处压力脉动的主频幅值和最大脉动幅值就越大。还可看出当导叶数等于9时蜗壳内径向各监测点处的压力脉动主频幅值最小，且各点处的压力脉动主频幅值和最大脉动幅值基本相等，而当导叶数等于7时蜗壳内径向各监测点处的压力脉动主频幅值和最大脉动幅值均最大。这是因为由图6⁃3可知导叶数等于7时叶轮进口的尾迹效应最显著，由此叶轮动静相互干涉作用就越强，所以蜗壳内径向各监测点处的压力脉动受叶轮动静相互干涉作用的影响就越大，且随着导叶数的增加导叶的过流面积逐渐减小，导叶进口速度逐渐增大，使导叶数等于11时蜗壳内径向各监测点处的压力脉动幅值也逐渐增加，但由于压力脉动主要受叶轮动静相互干涉作用的影响，所以当导叶数等于7时蜗壳内径向各监测点处的压力脉动主频幅值最大，而导叶数等于9时最小。

由表6⁃2还可以看出当导叶数等于9时蜗壳内径向的最大压力脉动主频幅值和最大脉动幅值分别为导叶数等于7时的0.43倍和0.66倍。可见，当导叶数等于9时可较大程度地降低蜗壳内径向的压力脉动主频幅值和最大脉动幅值，且此时蜗壳内径向各位置处的压力脉动主频幅值和最大脉动幅值基本相等。

3.不同流量下蜗壳内压力脉动分析

如图6⁃16所示为通过快速傅里叶变换得到的偏离最优工况下蜗壳内径向各监测点处的压力脉动频域图。从图6⁃16和图6⁃15可以看出在未加导叶时在不同流量下距离叶轮最近的监测点处除了主频幅值较大之外，其次主频幅值也较大，而添加导叶之后只有主频幅值较大。

不同流量下蜗壳内径向各监测点处的压力脉动主频幅值和最大脉动幅值见表6⁃3。

表6⁃3 不同流量下蜗壳内压力脉动的主频幅值和最大脉动幅值

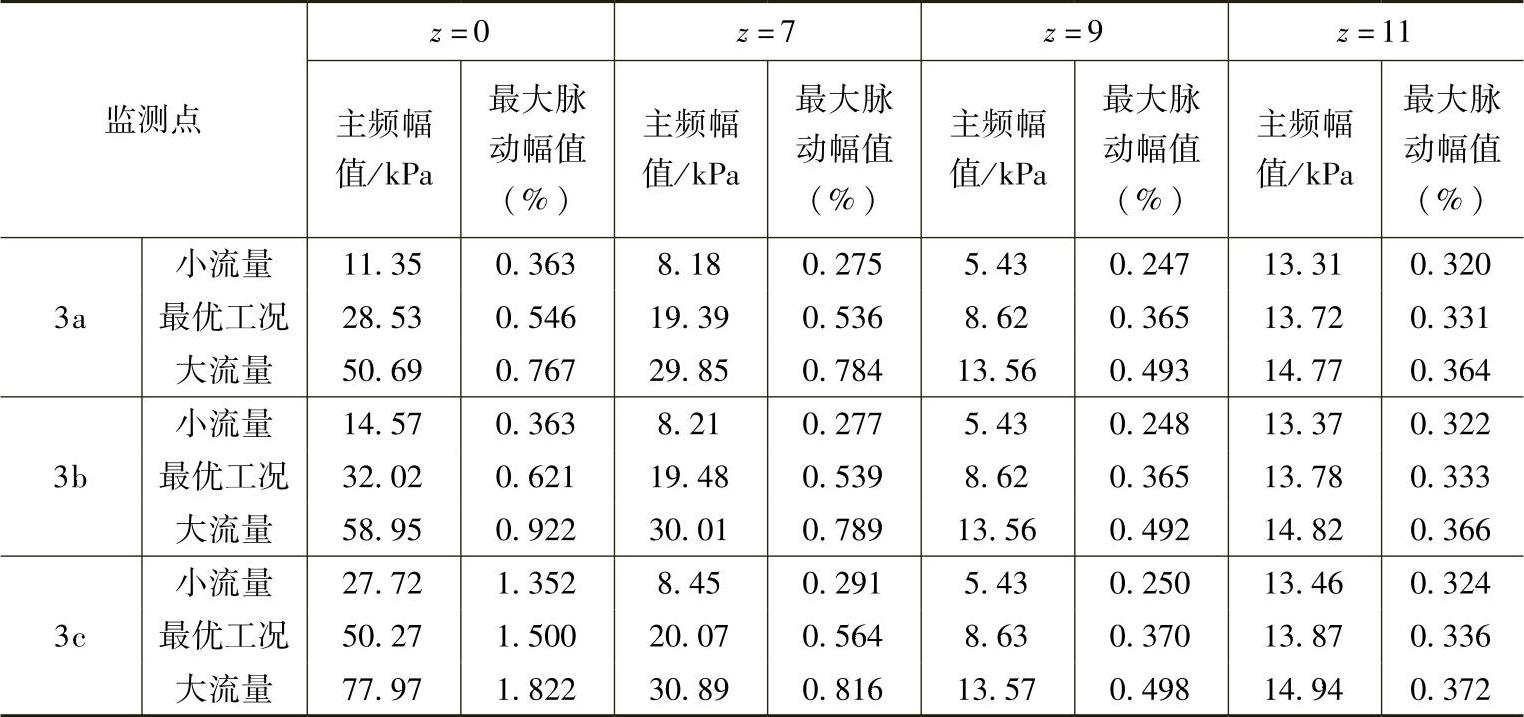
结合图6⁃16和表6⁃3可知在未加导叶时随着流量的增加蜗壳径向各监测点处的压力脉动主频幅值和最大脉动幅值随着距离叶轮进口越近其增加程度越大，而添加导叶后随着流量的增加蜗壳径向各监测点处的压力脉动主频幅值和最大脉动幅值随距离叶轮进口越近其增加程度变化不大。这主要是因为由图6⁃3可知，在无导叶时随着流量的增加叶轮进口速度逐渐增大且叶轮进口的尾迹效应越明显，叶轮进口叶片背面的漩涡就越大，这些都导致叶轮动静相互干涉作用越强，即蜗壳内压力脉动幅值越大，且距离叶轮进口越近压力脉动幅值增加越大。而添加导叶之后在不同流量下相对无导叶的情况，叶轮内液流流动均匀，也无漩涡产生，所以叶轮动静相互干涉作用也就越小。

还可以看出：添加导叶之后液力透平的流量越大，蜗壳内不同位置处的压力脉动主频幅值增加程度相对无导叶时越小，这主要是因为由图6⁃3可知随着流量的增加，无导叶时叶轮进口尾迹效应越明显且叶轮进口漩涡越大，导致叶轮动静相互干涉作用越强，而添加导叶后随着流量的增加叶轮进口液流的流动状态变化不大，所以叶轮动静相互干涉作用的强度变化较小，即蜗壳内压力脉动幅值增加较小。可见，添加导叶可以有效地降低大流量下蜗壳内的压力脉动幅值。

由图6⁃16和表6⁃3还可以看出随着流量的增加不同导叶数下蜗壳内径向各监测点处的压力脉动主频幅值和最大脉动幅值逐渐增大，且随着导叶数的增加这些监测点处的压力脉动主频幅值和最大脉动幅值的增加程度逐渐减小，在导叶数等于11时这些监测点处的压力脉动主频幅值和最大脉动幅值基本相等。这是因为由图6⁃3可知导叶数越多，叶轮进口的尾流效应越小，叶轮动静相互干涉作用越弱，蜗壳内压力脉动受到叶轮动静相互干涉作用的影响就越小，所以随

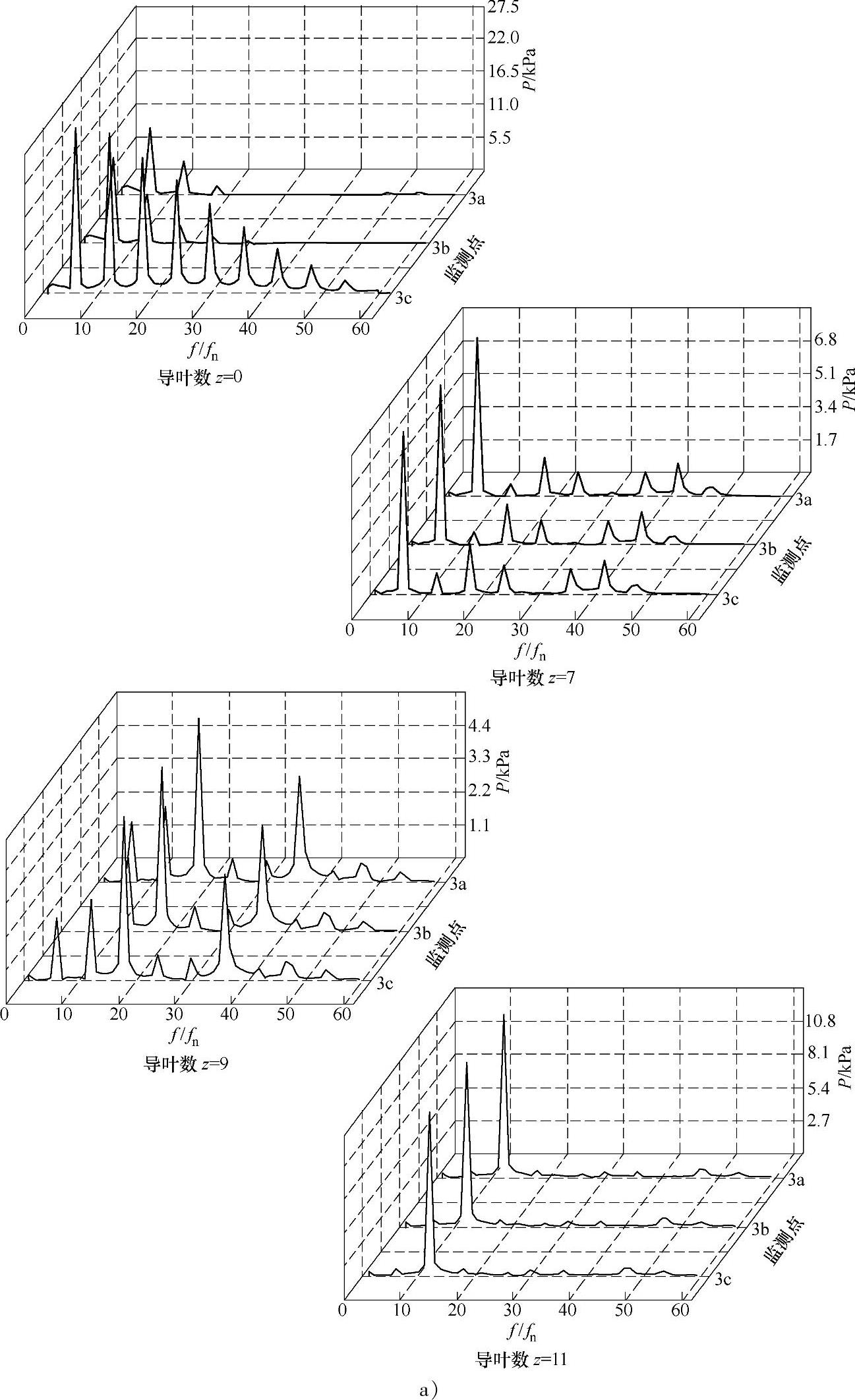
图6⁃16 偏离最优工况下

a）小流量

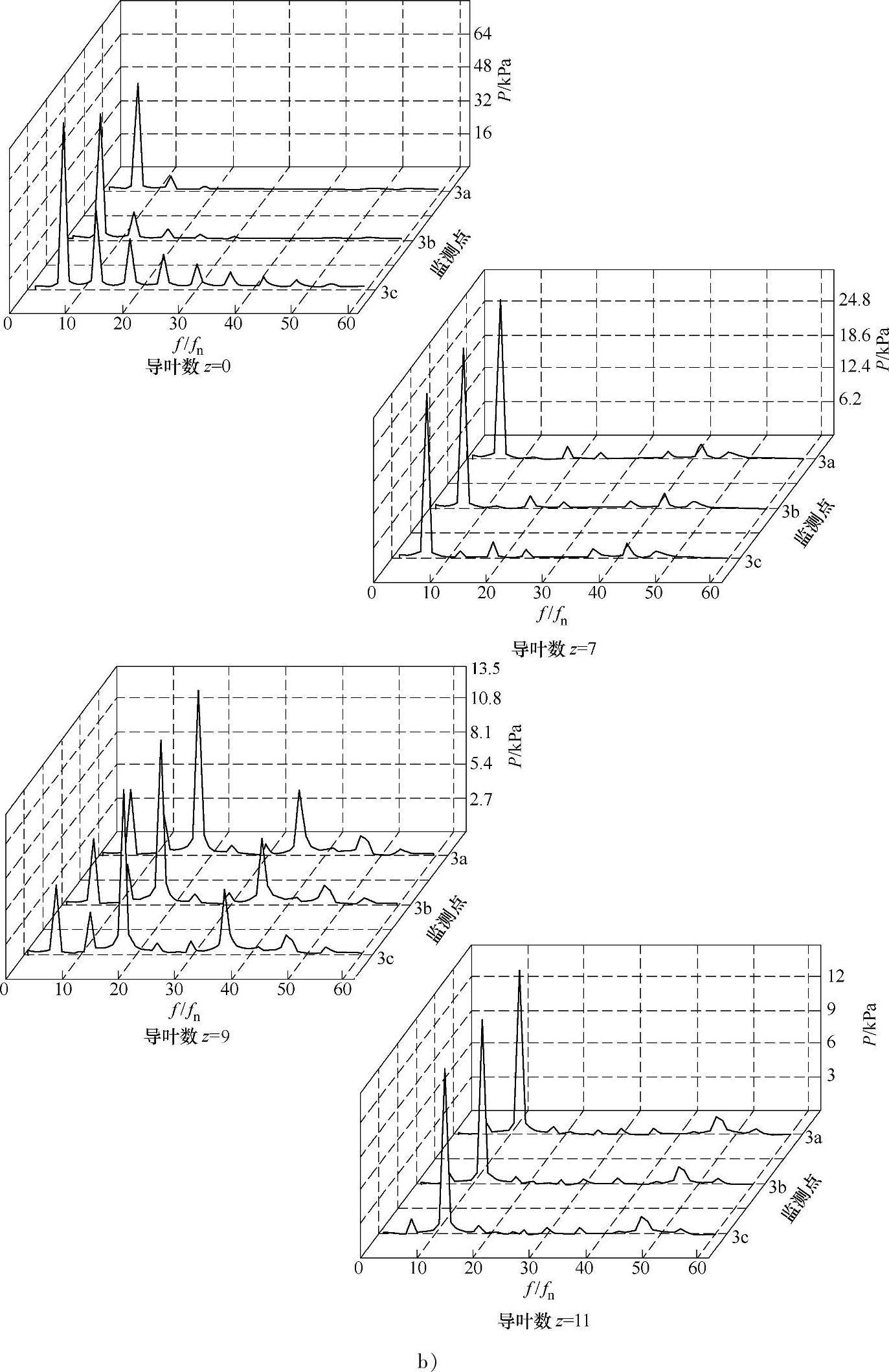
蜗壳内压力脉动频域图

b）大流量

着流量的增加导叶数越多蜗壳内压力脉动主频幅值的增加程度越小。又由上述研究结果可知导叶数越多，液力透平的水头越高，从而使蜗壳内最大脉动幅值的增加程度越小。

由表6⁃3还可以看出在小流量时当导叶数等于9时蜗壳内最大脉动幅值最小，这是因为在小流量时当导叶数等于9时液力透平蜗壳内的最大压力和最小压力的差值最小，而小流量时液力透平的水头变化不大，所以在小流量时当导叶数等于9时蜗壳内的最大脉动幅值最小。可见，当导叶数等于9时在不同流量下蜗壳内的压力脉动主频幅值最小。