蜗壳内流体能量转换特性分析

1.蜗壳不同截面上总压功率、静压功率和动压功率的时域特征

如图4⁃27和图4⁃28所示分别为液力透平在0.6Q_t、0.8Q_t、1.0Q_t、1.2Q_t、1.4Q_t和1.6Q_t6个工况下蜗壳各个截面上静压功率和动压功率、总压功率在叶轮旋转一个周期内的变化规律，各截面位置如图4⁃15所示。

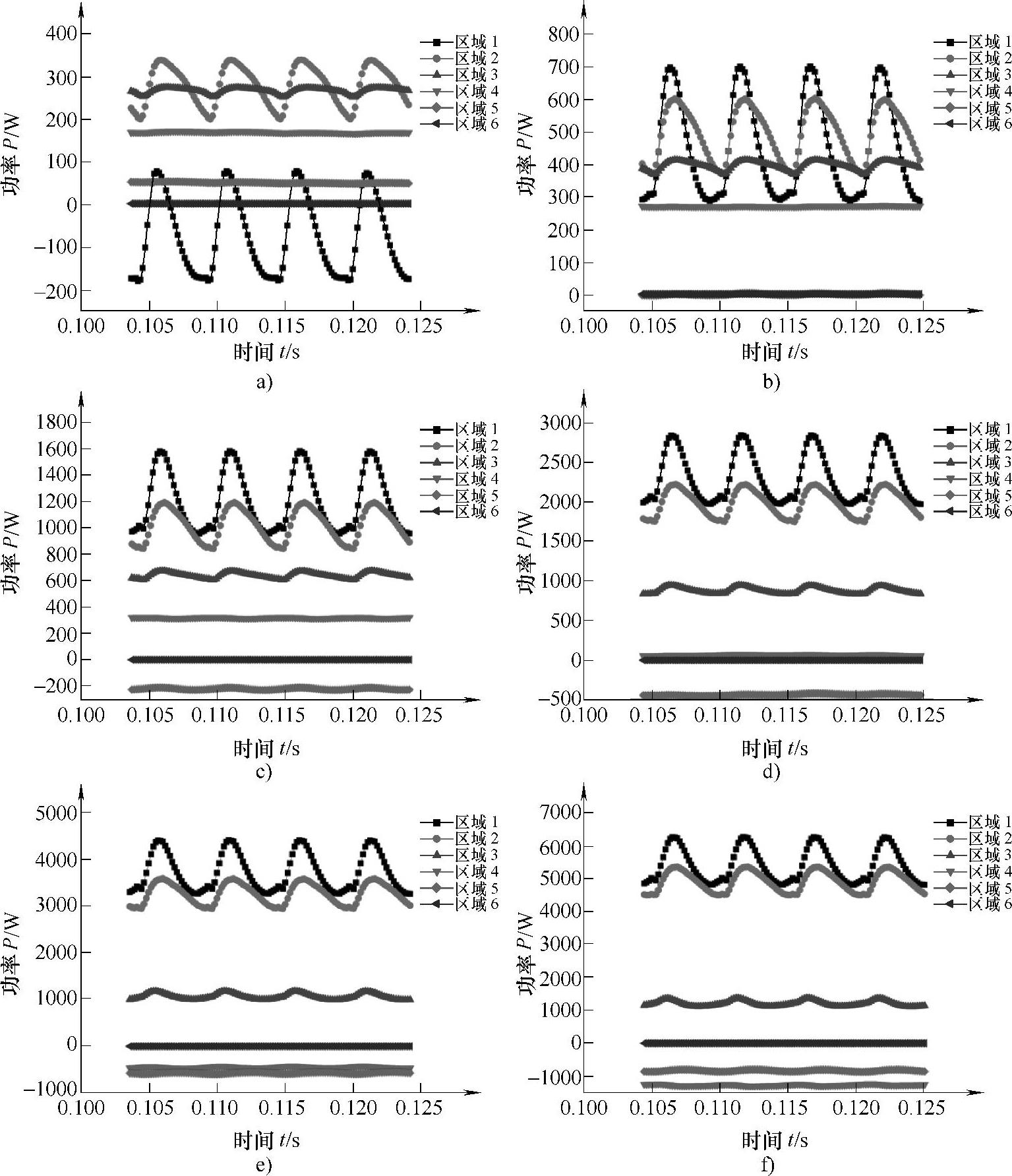
图4⁃26 叶轮不同区域所转换能量的时域变化规律

a）0.6Q_t b）0.8Q_t c）1.0Q_t d）1.2Q_t e）1.4Q_t f）1.6Q_t （彩图见书后插页）

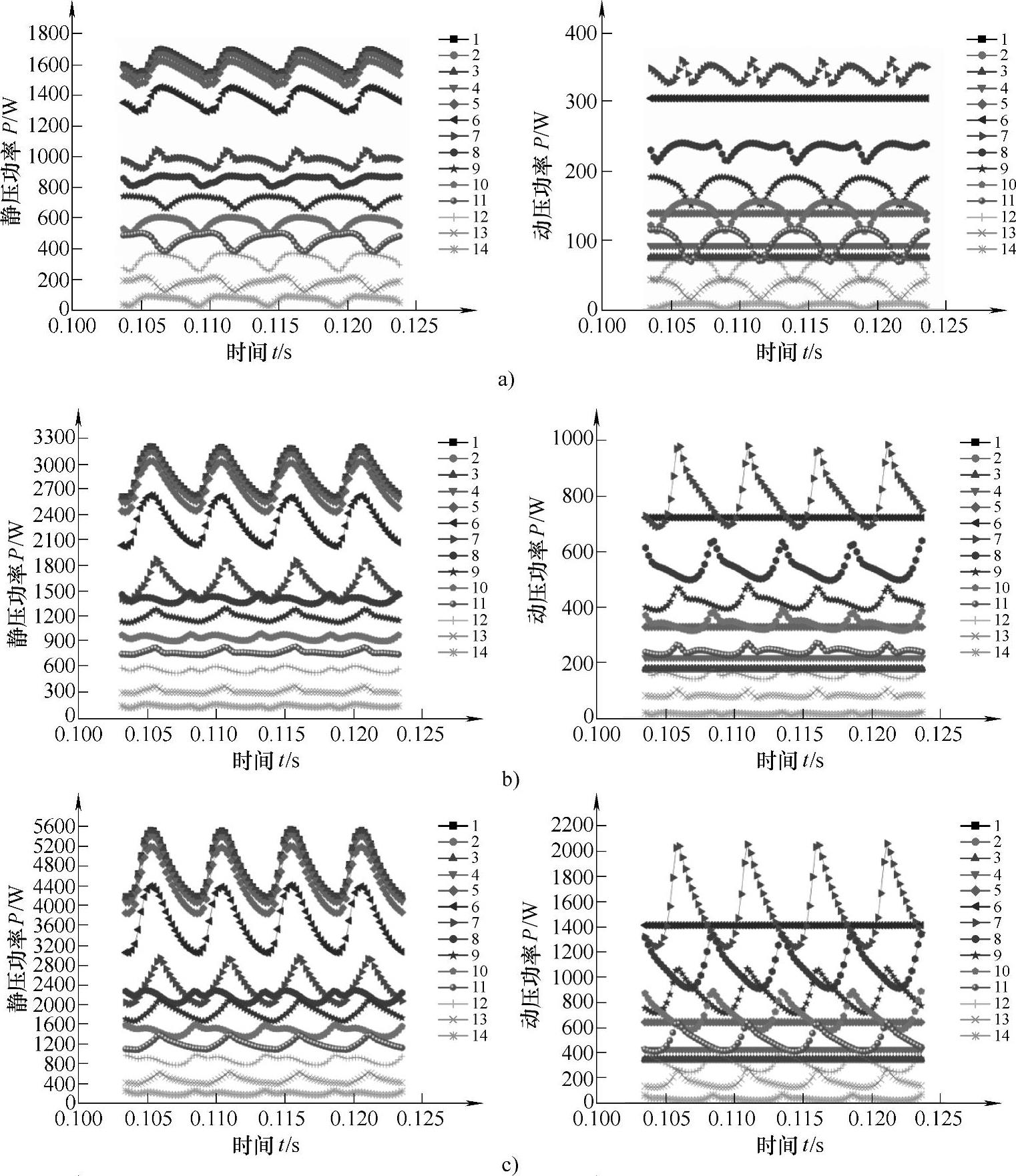
图4⁃27 蜗壳各个截面上静压功率和动压功率的时域变化规律

a）0.6Q_t b）0.8Q_t c）1.0Q_t （彩图见书后插页）

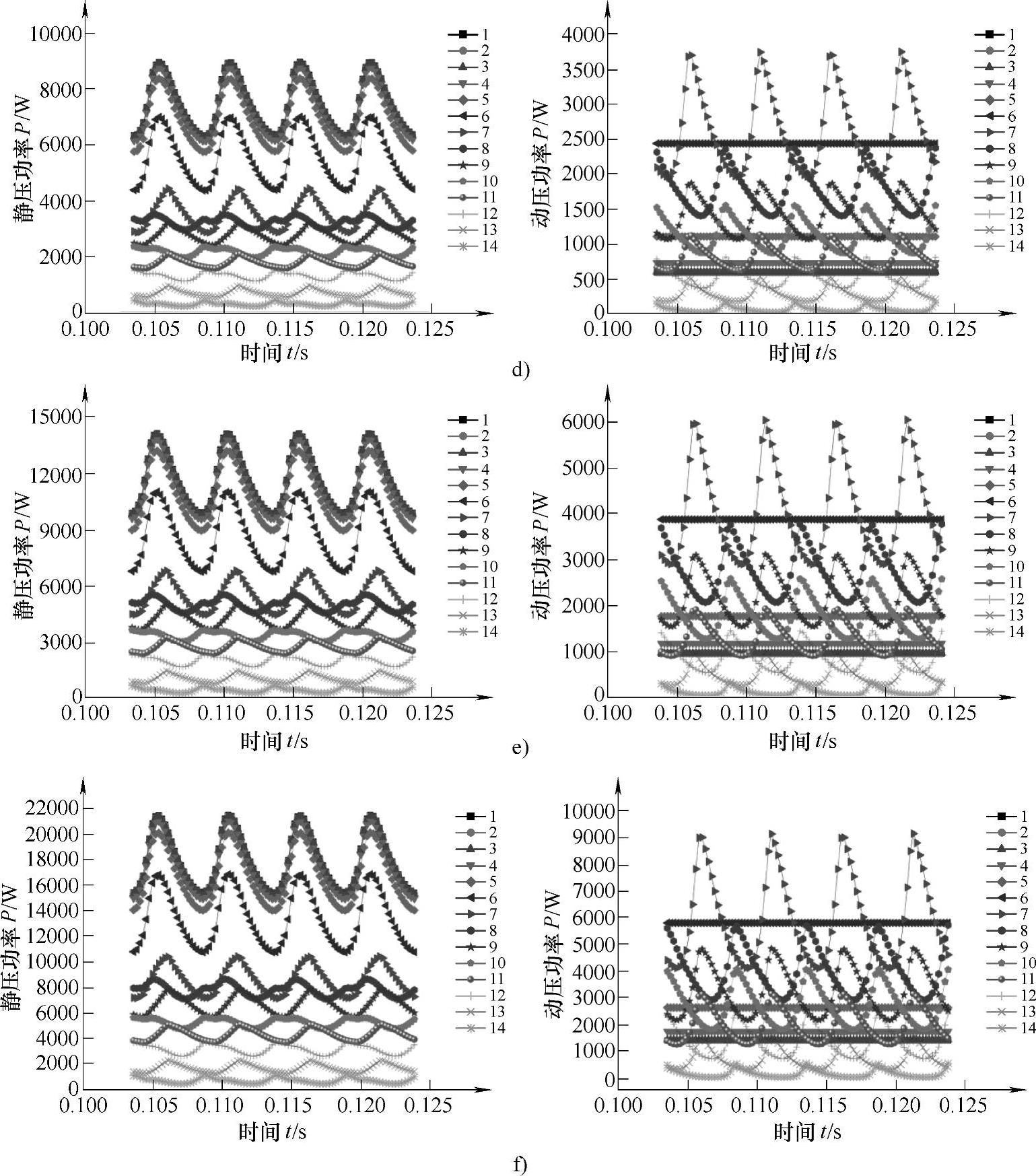
图4⁃27 蜗壳各个截面上静压功率和动压功率的时域变化规律（续）

d）1.2Q_t e）1.4Q_t f）1.6Q_t （彩图见书后插页）

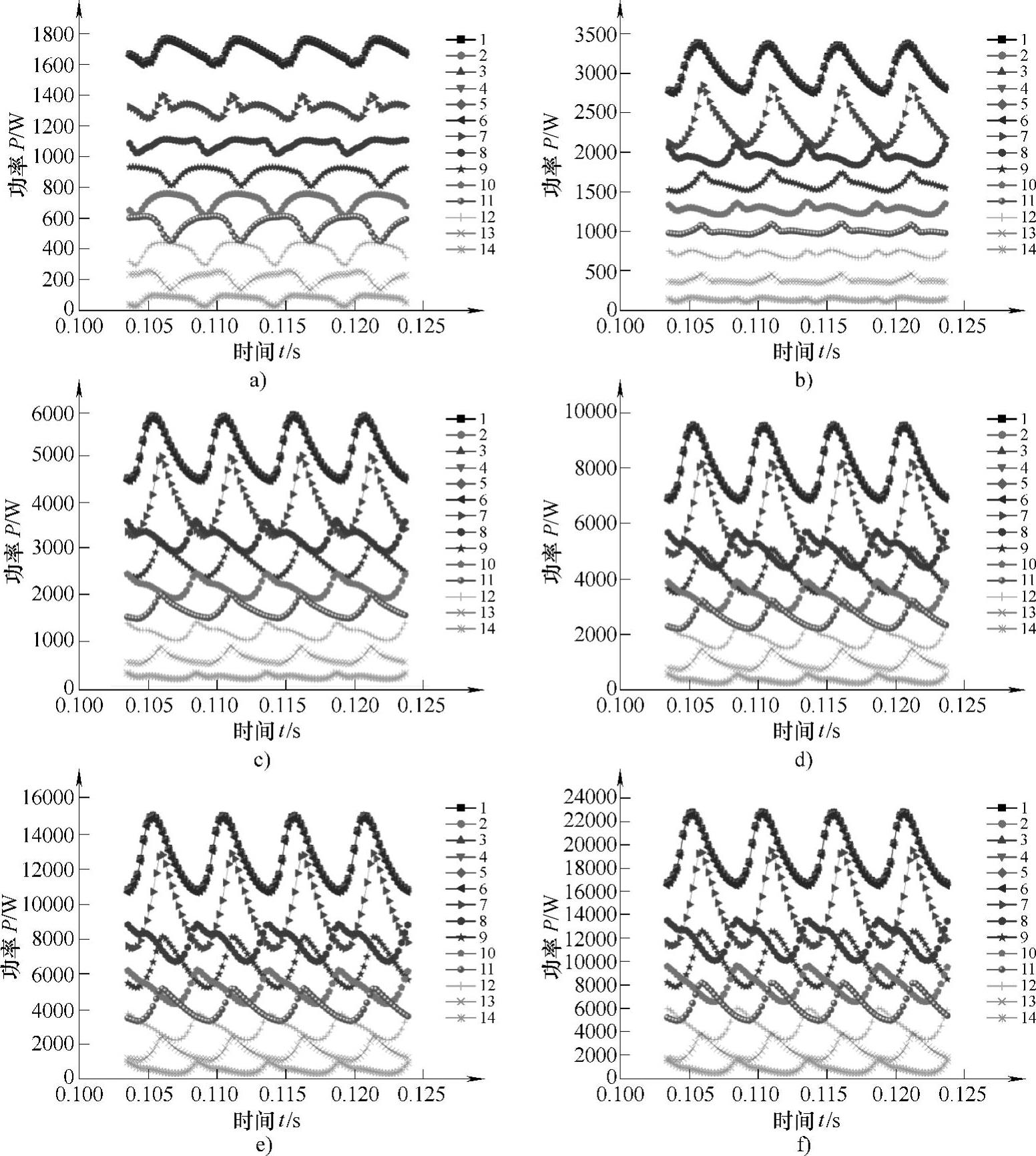
图4⁃28 蜗壳各截面上总压功率的时域变化规律

a）0.6Q_t b）0.8Q_t c）1.0Q_t d）1.2Q_t e）1.4Q_t f）1.6Q_t （彩图见书后插页）

从图4⁃27和图4⁃28可以看出，蜗壳各个截面上的静压功率、动压功率和总功率的平均值均随流量的增大而逐渐增大，且在叶轮旋转一个周期内，不同流量下各个截面上的静压功率、动压功率和总压功率均分别大体上呈现出相似的变化规律。

从蜗壳第1截面到第7截面（延伸段及收缩段），这7个截面上的静压功率在叶轮旋转一个周期内呈现出脉动数目与叶片数相等的周期性脉动规律，且静压功率沿各截面依次减小，而动压功率在前3个截面上基本相等，从第4截面开始逐渐增大，动压功率变大的原因是因为从第4截面开始，由于各过流断面面积的逐渐减小，流速会沿着各截面逐渐增大，所以从第4截面到第7截面，动压功率逐渐增大，此外，动压功率在前6个截面上几乎没有波动现象，从第7截面上开始出现波动现象。总压功率在叶轮旋转一个周期内呈现出的周期性脉动规律与静压功率的脉动规律类似，总压功率同样沿各截面依次减小，其中能量减少的部分即为流体从一个截面到另一个截面流动过程中损失的能量。

从蜗壳第7截面到第14截面（蜗形段），这8个截面上的静压功率、动压功率和总压功率在叶轮旋转一个周期内同样呈现出脉动数目与叶片数相等的周期性脉动规律，且静压功率、动压功率和总压功率的平均值均沿各截面依次减小，其中相邻两截面总功率的减小量等于流体从一个截面到下一截面流动过程中损失的功率与从相邻两截面间输出功率的两者之和。从图中还可以看出，静压功率、动压功率和总压功率在相邻两个截面上的脉动是不同步的，这是因为这8个截面上的功率的脉动与叶片通过各个截面的时间有关，本文中液力透平几何模型的叶片数是4个，可知相邻两叶片间的夹角为90°，而从蜗壳第7截面到第14截面的这8个截面上，相邻两截面间的夹角为45°，相间截面间的夹角为90°，从图中可以看出，相间截面上的模拟规律是同步的，即同时到达波峰或同时到达波谷。

通过4.1.2节蜗壳内流体能量转换特性的定常研究，初步明确了液力透平蜗壳内动、静压能的复杂转化过程。如图4⁃29所示为从蜗壳各个断面上静压能在总压能中所占的比例来说明蜗壳内动、静压能的非定常变化过程。

从图4⁃29可以看出，叶轮旋转一个周期时，除0.6Q_t工况外其他不同流量下蜗壳各个对应截面上静压能占总压能的比例具有相似的脉动规律，只是脉动的幅度随流量的增大而逐渐加剧，此外，各截面上静压能占总压能比例的脉动数目与叶轮叶片数相等。对于0.6Q_t工况，由于蜗壳内流动状况与大流量工况有所差别，从0.8Q_t工况下各截面上的流动特征也一定程度上能够看出大流量工况与0.6Q_t工况流动差别的过渡过程。从图中还可以看出，蜗形段内各截面上静压能占总压能比例的波动程度比进口延伸段（第1～3截面）和收缩段内截面上的波动剧烈，其中波动最大的是在大流量下蜗壳的第14截面，最大的相对波动幅值达到23%左右。值得注意的是，无论在小流量工况、最优工况，还是大流量工况，沿液体流动方向，静压能占总压能比例的变化规律是：从第1到第3截面，静压能所占比例几乎没有变化；从第3到第7截面，静压能所占比例逐渐下降，第7截面静压能所占比例降到最低，具体值分别为74.07%、66.28%、60.77%、57.65%、58.02%、59.61%，从这些数据中可以看出，从0.6～1.2Q_t工况，第7截面上静压能所占比例逐渐降低，而从1.2Q_t工况之后，静压能所占比例又逐渐增大，说明在小流量和大流量工况下存在着不同的能量转换过程，另外在这5个截面（第3～7截面），静压能所占比例下降梯度最大的是从第5到第7截面，从0.6Q_t到1.6Q_t分别下降了17.68%（91.75%→81.81%→74.07%，从5—6—7截面，下同）、22.86%（89.14%→76.03%→66.28%）、26.45%（87.22%→71.77%→60.77%）、28.32%（85.97%→68.98%→57.65%）、27.77%（85.79%→68.59%→58.02%）、26.54%（86.15%→69.39%→59.61%）；从第7到第14截面，静压能所占比总体上是呈上升趋势，其中上升梯度最大的是从第13截面到第14截面，从0.6Q_t到1.6Q_t分别上升了7.56%（84.36%→91.92%）、9.58%（78.31%→87.89%）、11.21%（73.91%→85.12%）、11.62%（71.44%→83.06%）、12.03%（70.76%→82.79%）、11.96%（71.52%→83.48%）。(https://www.xing528.com)

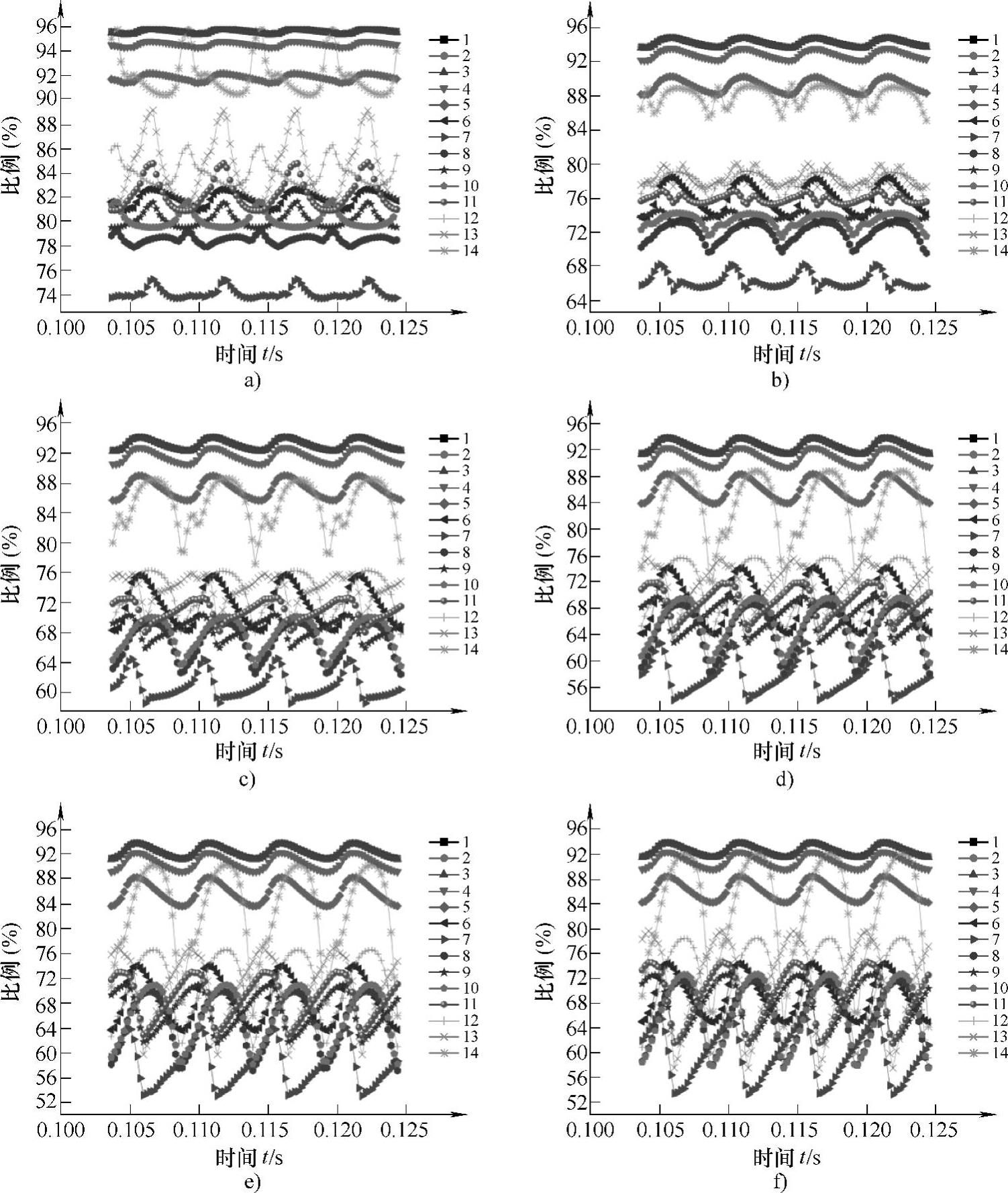
图4⁃29蜗壳截面上静压能占总压能的比例

a）0.6Q_t b）0.8Q_t c）1.0Q_t d）1.2Q_t e）1.4Q_t f）1.6Q_t （彩图见书后插页）

在蜗壳进口延伸段，由于过流面积相等，所以静压能占总压能的比例几乎相等，而在收缩段内，过流面积逐渐减小，因此静压能占总压能的比例也逐渐降低。从蜗壳收缩段进入到蜗形段后，因蜗壳与叶轮相通，会有一部分流体由蜗壳出口进入到叶轮中，因此各截面上的静压能所占比例的变化是这两部分作用的共同结果：一是蜗壳出口能量的比例关系，即蜗壳出口上静压能占总压能的比例；二是蜗形段内存在着一定的能量转化。

为了明确蜗形段内静压能占总压能比例的变化是否主要是由能量转化引起，如图4⁃30所示，给出了从蜗壳第8到第14截面上静压能占总压能比例的平均值，以及对应蜗壳出口面上静压能占总压能比例的平均值，图中第7和第8截面之间的蜗壳出口区域定义为出口1，第8和第9截面之间蜗壳出口区域定义为出口2，依此类推。

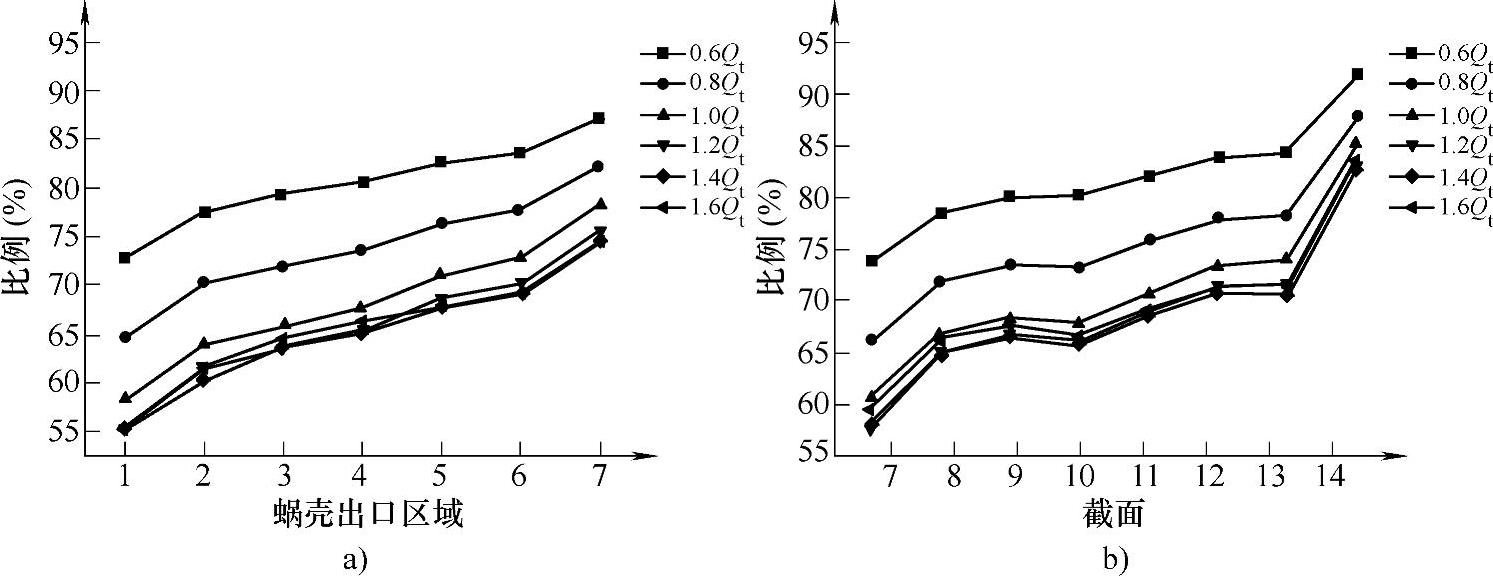
图4⁃30 静压能占总压能的比例

a）蜗壳出口 b）蜗壳截面

从图4⁃30可以看出，同一流量下，蜗壳出口与对应蜗壳截面上静压能所占比例的变化规律大体相似，均呈现出逐渐增大的趋势，但二者还是存在着一些变化幅度上的差异，这就说明在液力透平的蜗壳内存在着动、静压能的相互转化。在0.6Q_t工况下，对比蜗壳各个截面上与蜗壳出口截面上静压能占总压能的比例可以看出，从蜗壳第7截面到第10截面所在区域，动、静压能的转化不是特别明显，而从蜗壳第10截面到第14截面，静压能占总压能的比例从80.06%上升到91.92%，而对应的蜗壳出口截面上的静压能占总压能的比例则是从81.10%上升到87.14%，可以得出从蜗壳的第10截面到第14截面区域内有一定量的动压能转化成静压能。从图4⁃30中也可以看出，转化最为剧烈的是在第13截面到第14截面之间的区域；0.8～1.0Q_t工况范围内，蜗壳内的能量转化规律与0.6Q_t工况相似；而1.2～1.6Q_t工况范围内，从蜗壳第7截面到第13截面，动、静压能的转化相对较少，而在第13截面到第14截面之间存在着较为强烈的能量转化。

2.蜗壳不同截面上湍流耗散率的时域特征

如图4⁃31所示为不同流量下液力透平蜗壳各个截面上湍流动能耗散率在一个周期内的时域变化特征，截面位置如图4⁃15所示。

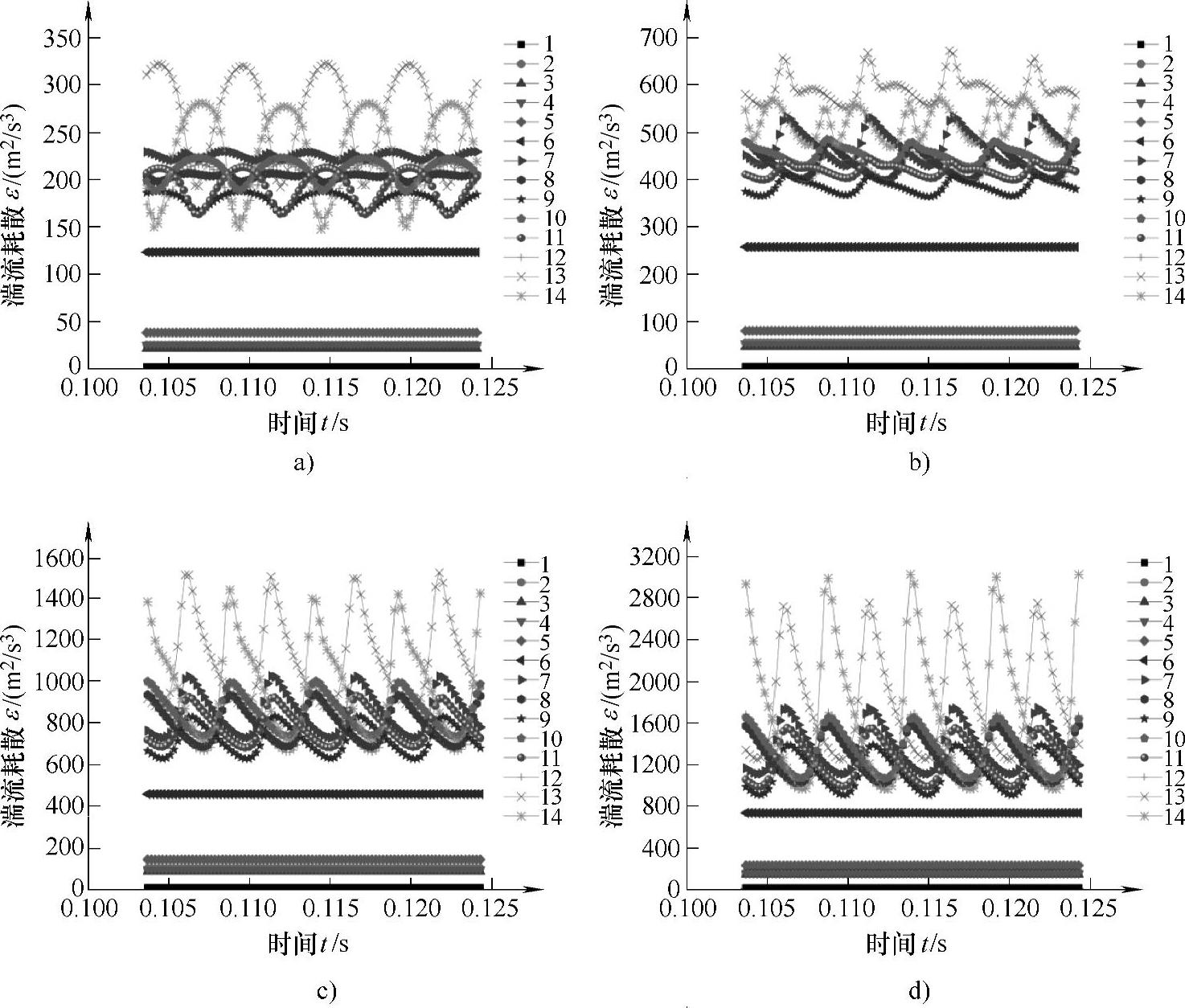
图4⁃31 叶轮不同截面湍流动能耗散率的时域变化规律

a）0.6Q_t b）0.8Q_t c）1.0Q_t d）1.2Q_t （彩图见书后插页）

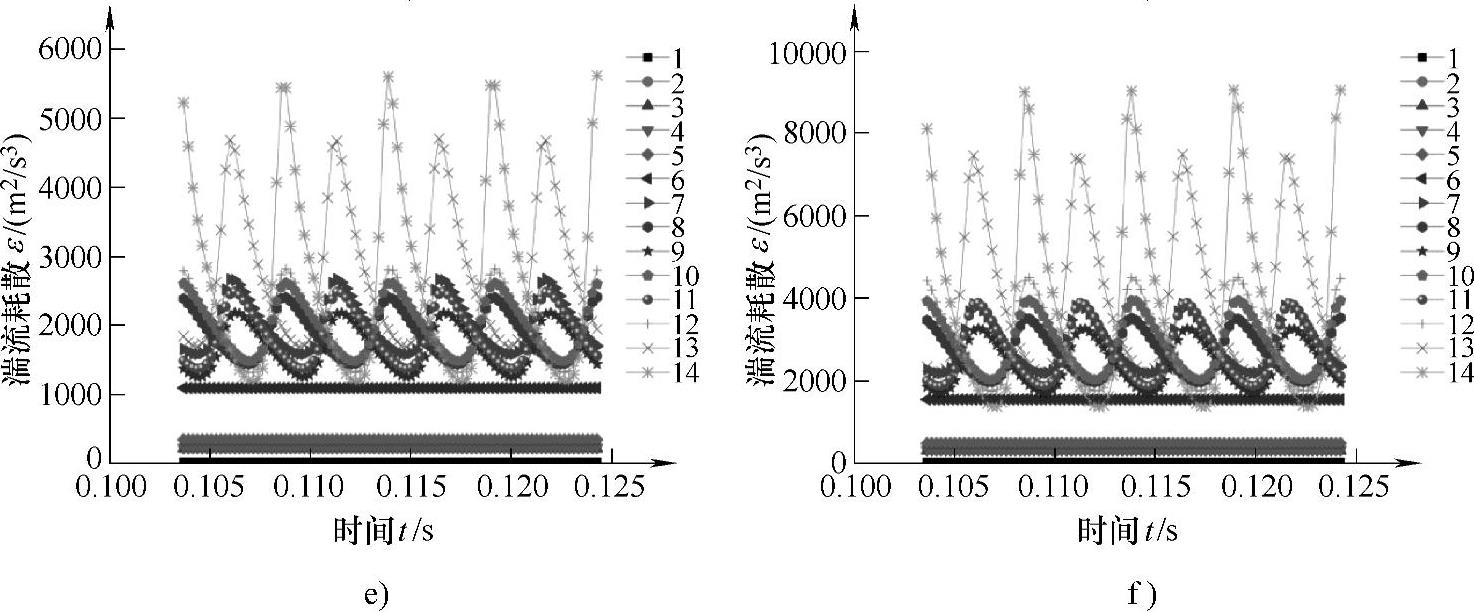
图4⁃31 叶轮不同截面湍流动能耗散率的时域变化规律（续）

e）1.4Q_t f）1.6Q_t （彩图见书后插页）

从图4⁃31可以看出，蜗壳各个截面上的湍流耗散率在不同流量下具有相似的时域变化规律，但脉动幅值不同。在蜗壳隔舌之前的各个截面上湍流耗散率均无随时间上的波动现象，而在隔舌之后的所有截面上均出现了波动数目与叶片数相等的波动变化；随流量的不断增大，蜗壳各个截面上的湍流动能耗散率无论是平均值还是波动幅值均逐渐增大。从图中也可以看出，蜗壳蜗形段内的湍流耗散值大于蜗壳延伸段及收缩段内的湍流耗散值。在蜗形段内，湍流耗散相对较大的是第7、13和14截面，在小流量工况和最优工况下，第13截面上的湍流耗散率最大，其次是第14截面，而在大流量工况下，第14截面上的湍流耗散率达到最大，同时在蜗壳中波动相对较大的也是第13和14截面，因此在蜗壳这两个截面之间区域的损失相应比较大。通过对蜗壳各截面上湍流动能耗散时域特征的分析，可为液力透平蜗壳截面以及隔舌的合理设计提供一定参考。