近似曲边四边形和三角形求解SDCOA方法

在图3⁃8中为求解S_DCOA，曲边四边形ADCO被近似的四边形A′D′C′O′所代替，曲边三角形ABO被近似的三角形A′B′O′所代替，如图3⁃8所示。

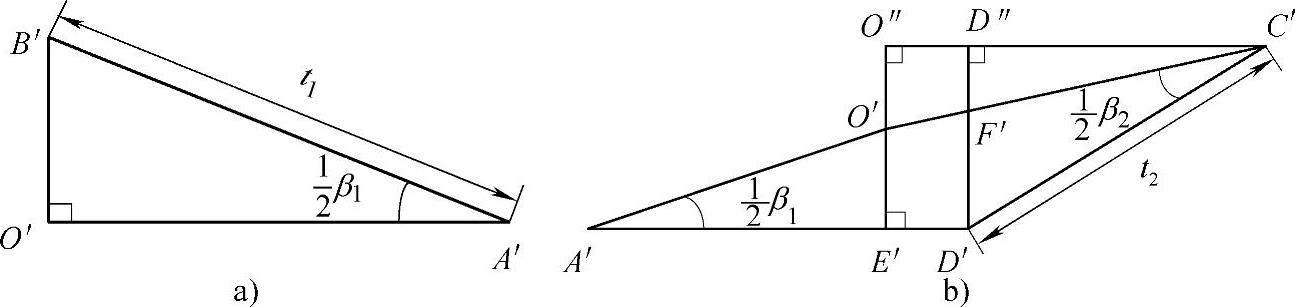
图3⁃8 近似图形

a）近似的三角形A′B′O′b）近似的四边形A′D′C′O′

过O′作O′E′⊥A′D′于点E′，过C′作C′O″⊥O′E′交于E′O′的延长线于点O″，然后过D′作D′D″⊥O″C′于点D″，交O′C′于点F′。

在曲边四边形ADCO和曲边三角形ABO中，CO线、BO线和AO线均与轴向漩涡流线相垂直，因此

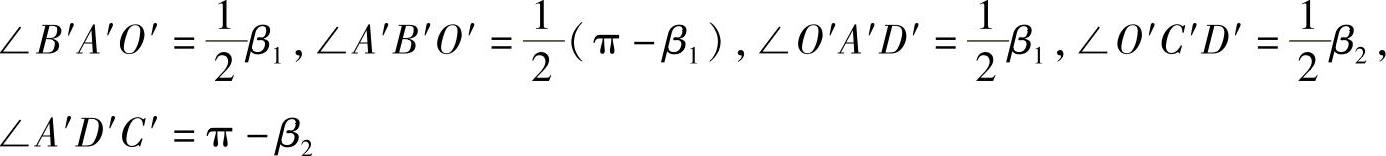
所以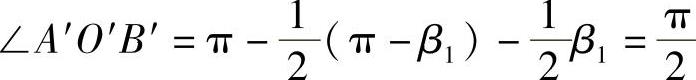

可见，三角形A′B′O′为直角三角形。令A′B′=t₁，C′D′=t₂，则有

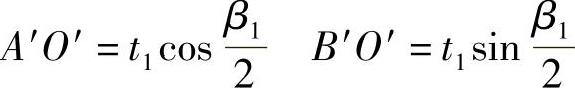
在四边形A′D′C′O′中

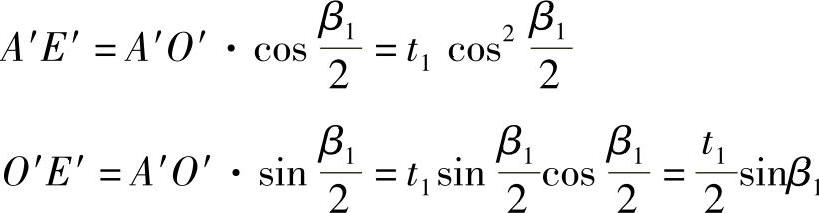
因此图3⁃8b中的直角三角形A′E′O′的面积

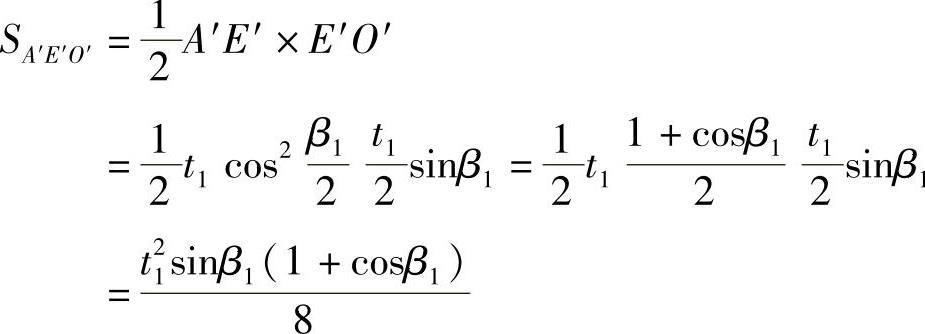
又在直角梯形E′D′C′O″中

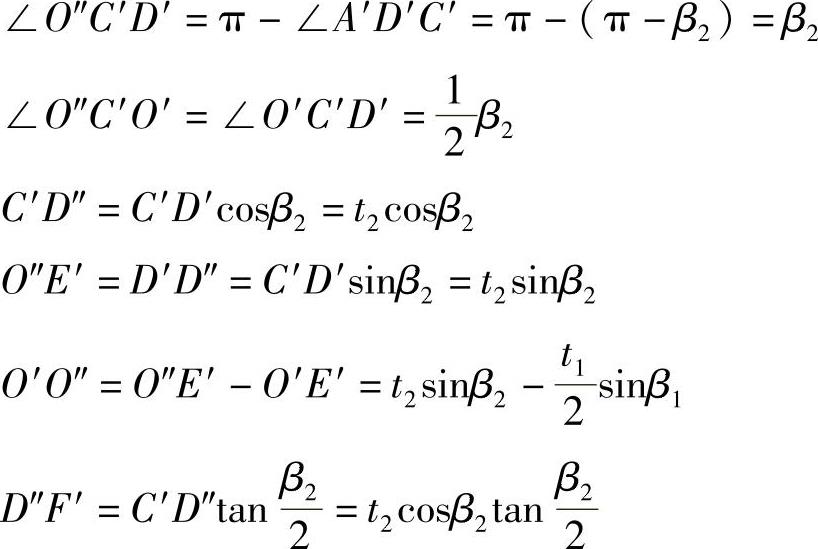
由于ΔC′D″F′与ΔC′O′O″相似，则有：

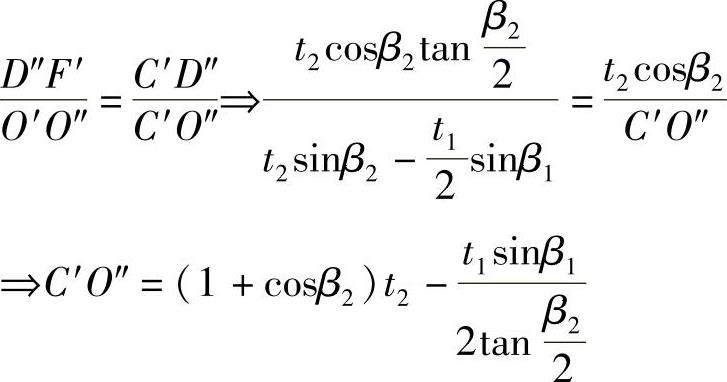
所以：

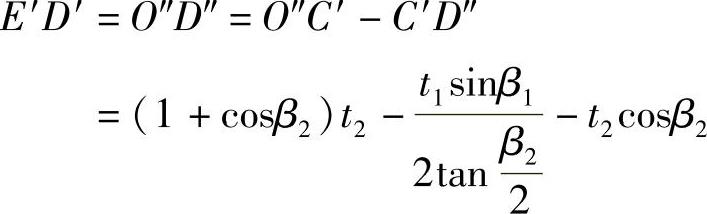
经整理，得

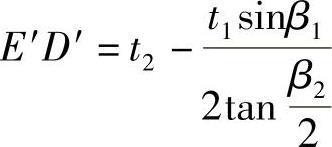
因此图3⁃8b中直角梯形O″E′D′C′的面积

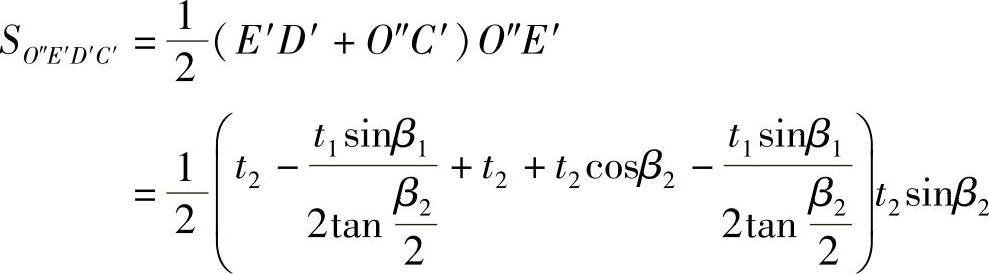
经整理，得

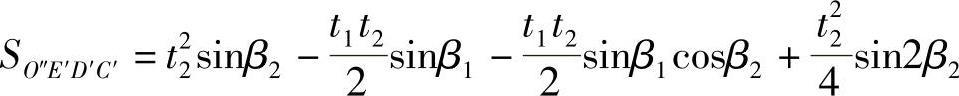
又图3⁃8b中直角三角形O″O′C′的面积

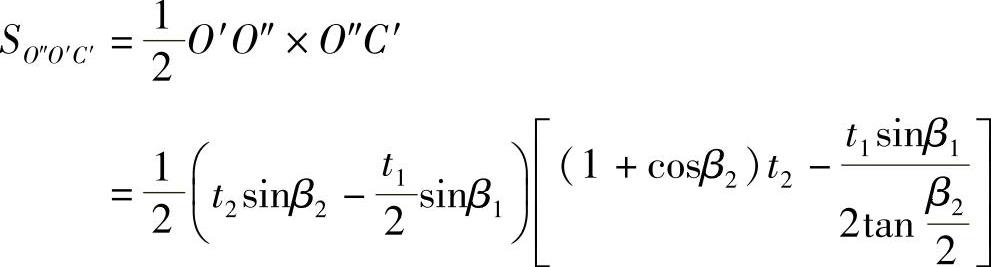
经整理，得

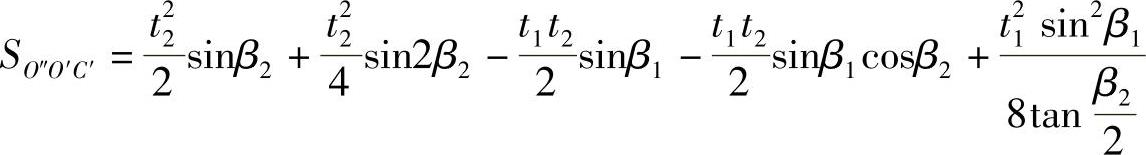
所以在图3⁃8b中四边形O′E′D′C′的面积

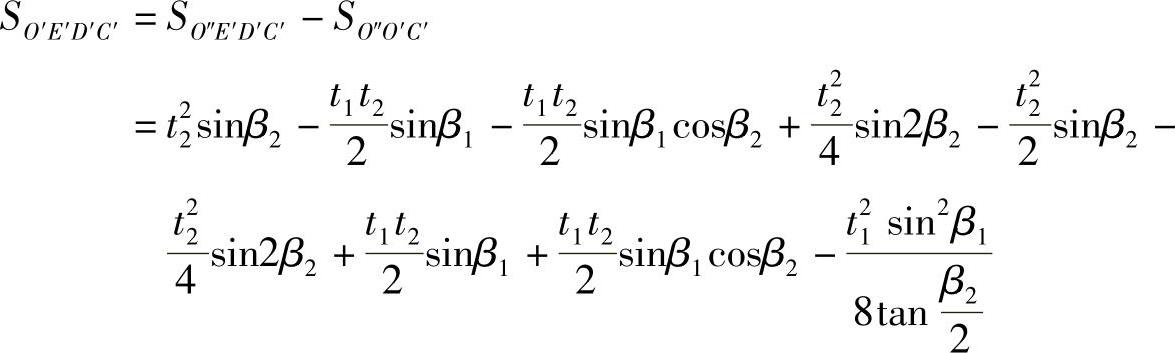
经整理，得

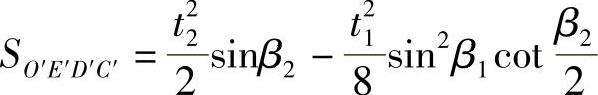(www.xing528.com)

因此曲线DCOAD所围的面积

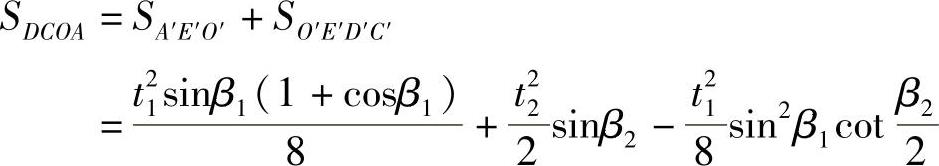
经整理，得

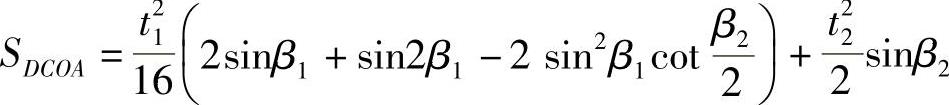
令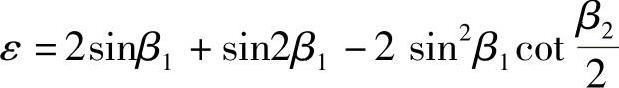，则

将式（3⁃36）代入式（3⁃8）

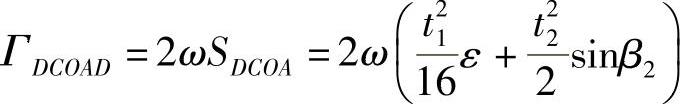
Γ_DCOAD等于封闭围线每段围线环量之和，于是有

Γ_DC=Γ_DCOAD^-ΓAD （3⁃37）

由于Δw在距离叶片较近处较小，而在两叶片的中间位置较大，所以可假设在液力透平的叶轮流道内其相对速度沿叶片工作面从叶轮进口到出口均匀变化。因此在计算Γ_AD时可取叶轮进出口相对速度的平均值w_AD。

即

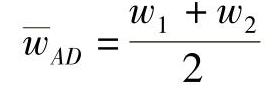
又

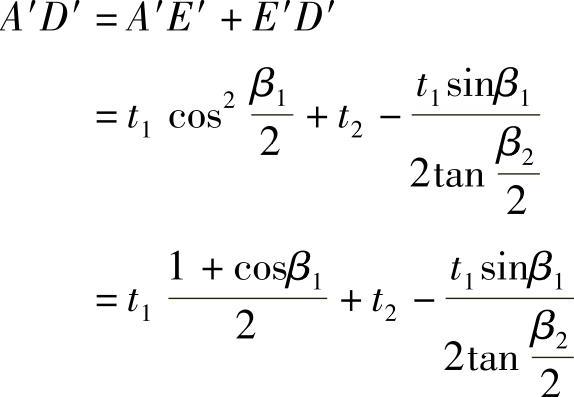
所以边AD上的环量

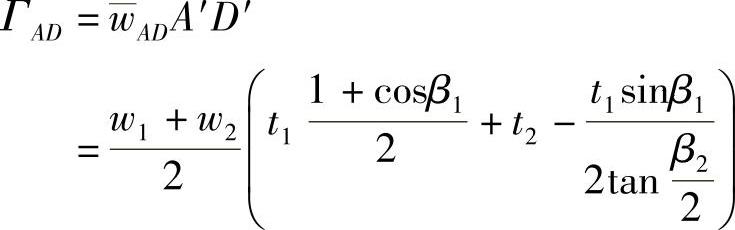
由进出口速度三角形可知

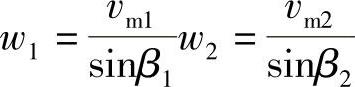
所以

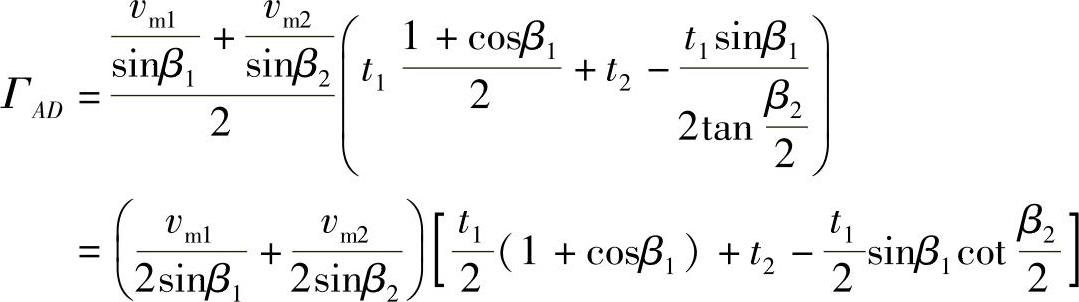
即边DC上的环量

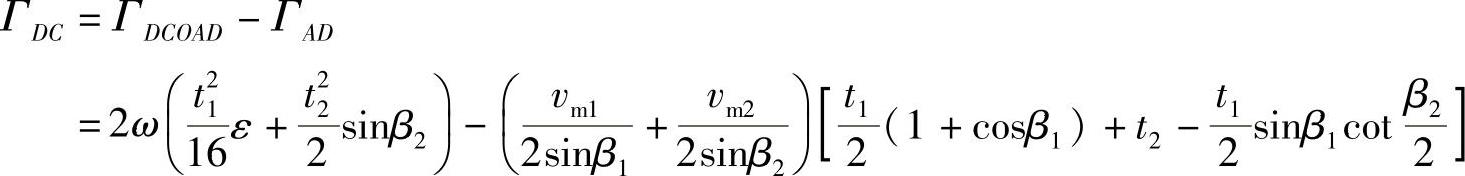
所以在圆周速度方向上，当叶片数有限时，叶片出口的绝对速度分量的偏移量即液流的滑移量

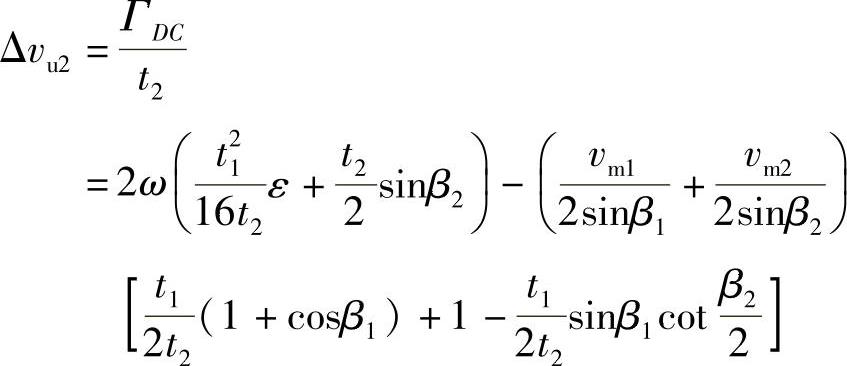
又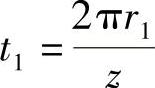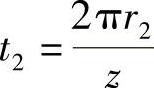，，则

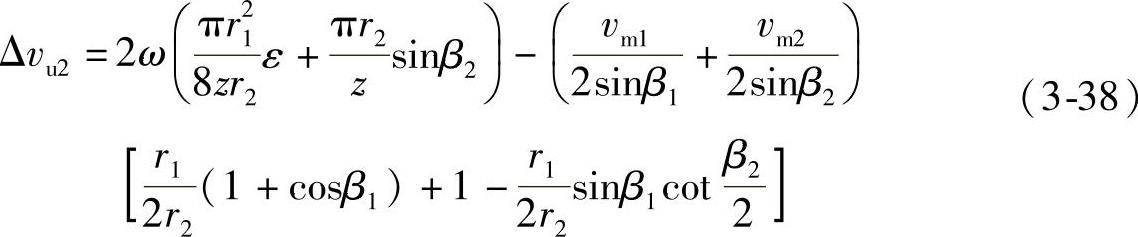
设在假设四的条件下液力透平叶轮出口的滑移系数为λ₄，则

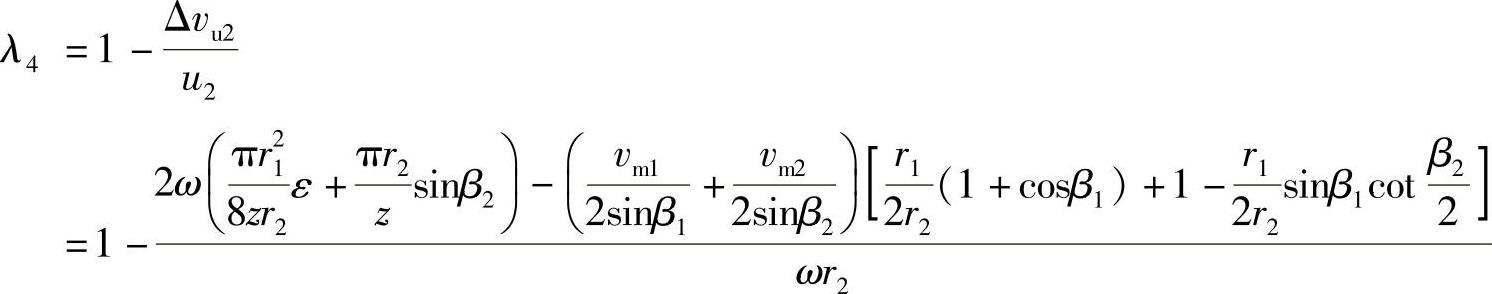
经整理，得

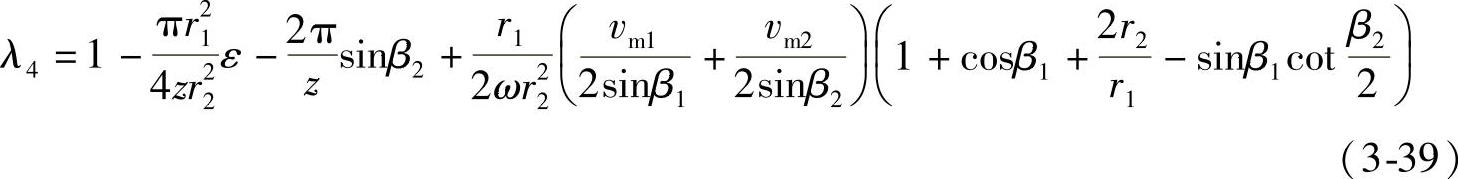
式（3⁃39）中的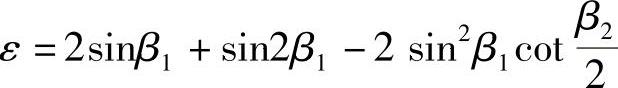

式中r₁、r₂——分别为叶轮进出口的半径（m）； z——叶轮叶片数； v_m1——在有限叶片数下叶片进口的绝对速度的轴面分量（m/s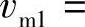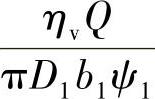），，且D₁=2r₁为叶轮的进口直径（m）；b₁为叶片的进口宽度（m）；η_v为液力透平的容积效率；Q为透平流量（m³/s）；ψ₁为叶片进口排挤系数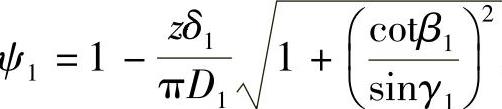，，γ₁为轴面截线与轴面流线的夹角（°），一般γ₁=60°～90°；δ₁为叶片进口的真实厚度（m）；v_m2——在有限叶片数下叶片出口的绝对速度的轴面分量（m/s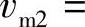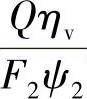），且F₂为叶片出口轴面液流的过水断面面积（m²），F₂=2πRb，b、R分别为在叶轮的轴面投影图中小流道的宽度和半径（m）；ψ₂为叶片出口的排挤系数，取ψ₂=0.85。