如何计算向心叶轮出口滑移系数？

目前，可以采用试验测量、叶轮数值计算和简单的解析计算等方法得到滑移系数。前两种方法需要完整的叶轮几何信息和复杂的操作，才能得到滑移系数，不便于设计初始阶段或选型使用。解析计算则通过简单的叶轮内部环流分析和适当的假设得到滑移系数，需要叶轮几何信息少，又有一定的准确性，便于工程应用，因此本章采用这种方法。

叶轮的流动滑移主要是由叶轮旋转引起的，因此可以仅考虑叶轮进、出口用圆柱面封闭起来的漩涡强度为2ω的二维有势流动，即相对涡流或轴向漩涡或相对环流，如图3⁃7所示。该环流在叶轮进口和出口边引起的诱导速度分别就是进口和出口的滑移速度。从流体力学角度，需要采用数值方法求解流函数的Poisson方程或势函数的Laplace方程才能得到图3⁃7所示的环状流线和等势线[30]。

为了便于解析计算，假设环流的漩涡中心O是∠DAB、∠ABC和∠BCD平分线的交点，这些角平分线本身是等势线，叶片工作面AD、背面BC、进口AB和出口DC上的漩涡诱导速度各自等于常数。

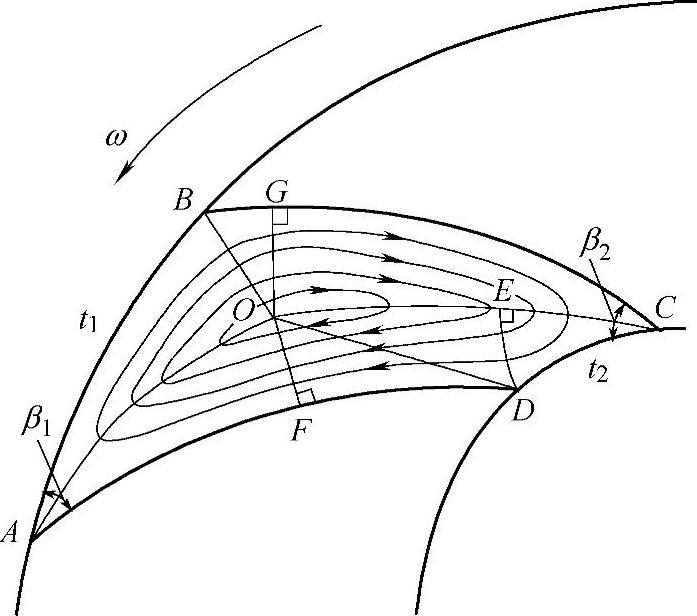
图3⁃7 轴向漩涡

注：t₁为流道进口AB的长度（m）；t₂为流道出口CD的长度（m）；β₁为叶片进口角（°）；β₂为叶片出口角（°）。下同。

然后取含有叶片工作面AD或背面BC或进口AB或出口DC流线及等势线所围成的曲线的速度线积分。根据斯托克斯定理（即在涡量场中沿任意封闭曲线的速度环量与以该曲线为周界所围曲面上的涡通量相等）计算该流线上的流体速度，其中进口AB或出口DC上的流速分别是进口和出口滑移速度。

由于OD不是等势线，所以计算叶轮出口滑移速度Δv_u2遇到了困难。取环线ADCO做速度线积分，结果流线AD的未知速度Δv_CD也出现在斯托克斯定理的方程中，造成了一个方程两个未知数无法求解的局面。(www.xing528.com)

为此，必须对Δv_u2和Δv_CD之间的关系做进一步分析和假设。本章中提出四种不同的假设：

假设一：假设AD上的诱导速度Δv_CD等于DC上的诱导速度Δv_u2，即Δv_CD=Δv_u2；

假设二：假设AD上的诱导速度Δv_CD与DC上的诱导速度Δv_u2存在一比值k，且k等于曲边三角形ADO的面积除以曲边三角形DOC的面积，即；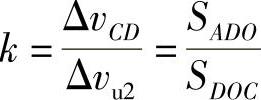

假设三：过D点作曲线DE，使DE⊥OC，垂足为E，假设该曲线DE与轴向漩涡的流线相垂直。

假设四：假设在液力透平的向心叶轮流道内其相对速度沿叶片工作面从叶轮进口到出口均匀变化。

下面具体给出四种假设条件下滑移系数的计算方法。