【摘要】:为了证明液力透平向心叶轮内轴向漩涡运动的存在,特引用一例子予以证明:图31 圆形容器内的相对运动一个充满液体的圆形容器以一定的角速度ω绕坐标中心O旋转,如图31所示。在有限叶片数的流道内除了相对轴向漩涡运动之外,还存在一个均匀流,因为当叶轮不动时,在叶轮流道内相对速度从叶片的工作面到背面是均匀分布的,如图33a所示。
在有限叶片数的叶轮流道内,不但存在一个径向的均匀流动,而且还有一个相对轴向漩涡运动[29]。为了证明液力透平向心叶轮内轴向漩涡运动的存在,特引用一例子予以证明:
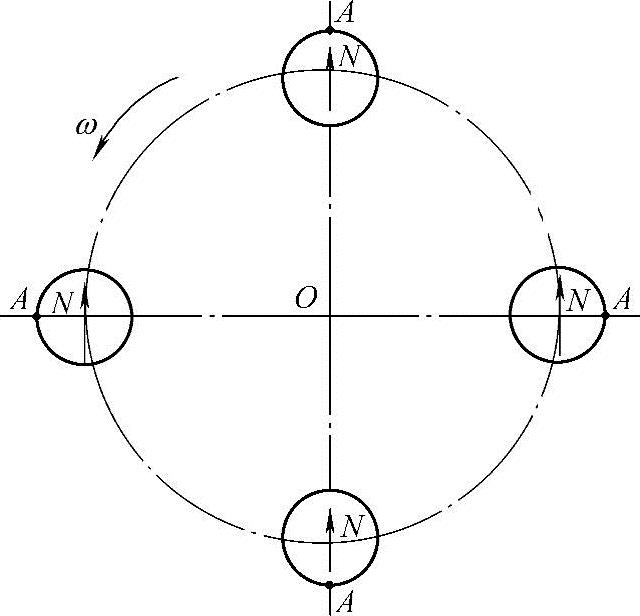
图3⁃1 圆形容器内的相对运动
一个充满液体(理想液体)的圆形容器以一定的角速度ω绕坐标中心O旋转,如图3⁃1所示。
在图3⁃1中,A点在容器上,而浮在液体上的指针指着固定坐标系统的N点方向。当容器旋转时,液体由于本身惯性保持着原来的状态,箭头始终指着N点,这就形成了液体对于容器有个相对的旋转运动,旋转角速度也等于ω,但与容器旋转方向相反。
同理,如果将叶轮流道进口和出口封闭起来,叶轮在旋转时,流道中的液体也同样有一个相对的旋转运动,这种运动就称为相对轴向漩涡运动,如图3⁃2所示。即对于液力透平而言,在向心叶轮流道中也同样存在与叶轮旋转角速度大小相等,方向相反的相对轴向漩涡运动。(https://www.xing528.com)
在有限叶片数的流道内除了相对轴向漩涡运动之外,还存在一个均匀流,因为当叶轮不动时,在叶轮流道内相对速度从叶片的工作面到背面是均匀分布的,如图3⁃3a所示。而当叶轮流道进出口封闭且叶轮旋转时,叶轮流道内的相对运动变为漩涡运动,且该漩涡运动的方向与叶轮的转向相反,则总的相对运动为上述两种运动之和,如图3⁃3b所示。
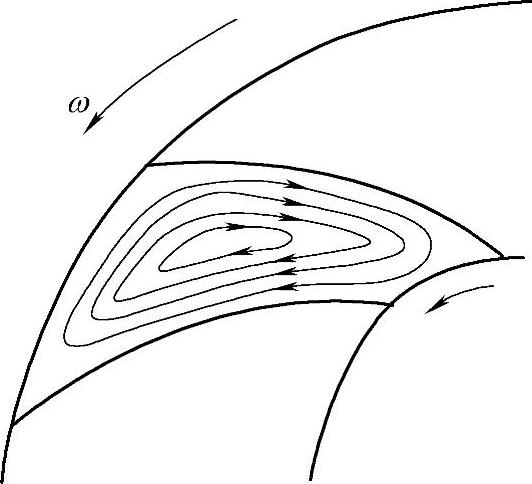
图3⁃2 流道内的相对轴向漩涡运动
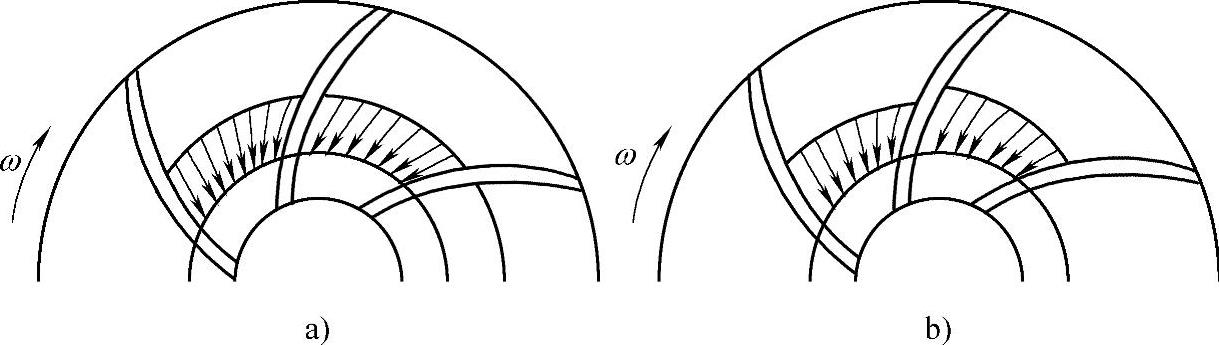
图3⁃3 叶轮流道内流体的相对运动
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




