流量水头特性曲线分析

如图1⁃10所示，将透平内部流动区域划分为图示三个部分：蜗壳、叶轮和尾水管。则由前面内容可知，透平的实际水头等于透平的理论水头与锅壳、叶轮和尾水管内部水力损失之和，即

H=H_t+∑h （1⁃26）

式中 ∑h=h_蜗壳+h_叶轮+h_尾水管 （1⁃27）

液力透平内部的水力损失可分为两部分，一部分是流体与流道摩擦引起的摩擦损失，记为h_f，与流量二次方成正比，即

h_f=KQ²（1⁃28）

图1⁃10 透平内部流动区域划分

另一部分是液流与叶轮进口冲击引起的冲击损失h_s，冲击损失和流量与最优工况流量的偏离值ΔQ的二次方成正比，在最优工况时近似为零，即

h_s=KΔQ² （1⁃29）

又由液力透平基本方程式和叶轮进出口速度三角形（图1⁃9），设叶片数为无穷时液力透平的理论水头为H∞，则有

叶片数为有限时，考虑叶轮内部滑移（关于滑移理论本书后续章节将详细讲述），液力透平的理论水头为(www.xing528.com)

H_t=λH∞ （1⁃31）

式中 λ——滑移系数。

故由式（1⁃30）和式（1⁃31）知，液力透平的理论水头与理论流量呈线性关系，即

H_t=KQ_t （1⁃32）

由式（1⁃29）和式（1⁃32）可知，液力透平的流量与水头之间的关系可以表示为

H=f（Q²，Q_t） （1⁃33）

如图1⁃11所示为液力透平流量水头特性曲线的组成。

图中q为由于口环间隙、平衡孔、机械密封等引起的泄漏量。高压液体通过口环间隙、平衡孔、机械密封等的泄漏会引起液体压力能的损失，其压力能的损失量在图中用ΔH_t表示。

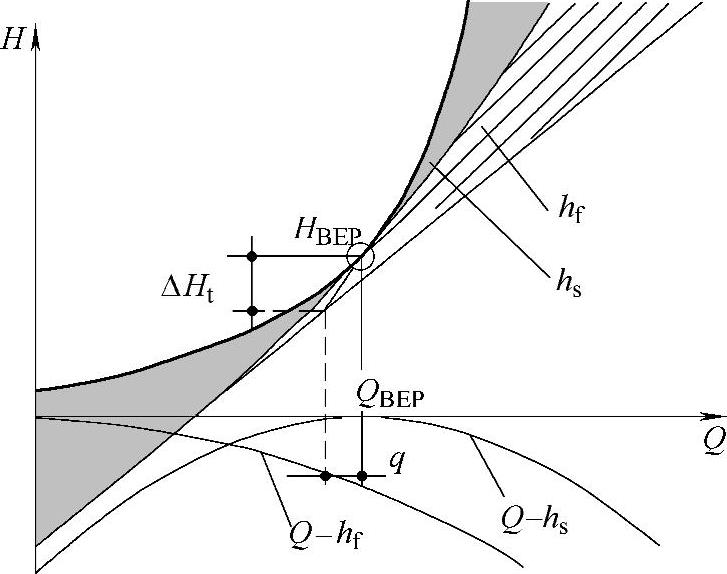
图1⁃11 液力透平流量水头的特性曲线