如何衡量相似性？

在上述方法中，都要使用距离这个概念。这种距离实际上是在特征空间已经存在的情况下，每个像素之间的相似程度。距离近的表明两个类之间，或者两个像素之间很相似；距离远的表示不相似。

因此，距离是判定相似性的度量工具。分类是确定像素距离哪个点群中心较近，或落入哪个点群范围可能性大的问题。像素与点群的距离越近，那么属于该点群的可能性越高。按照一定的准则，当距离小于一定值时，像素被划分给最近的点群。每个点群为一个类。

根据距离的分类是以地物光谱特征在特征空间中以点群方式分布为前提的。也就是说，假定不知道特征的概率分布但认为同类别的像素在特征空间内完全呈现成集群，每个集群都有一个中心。这些集群内点的数目越多，亦即密度越大或点与中心的距离越近，就越可以肯定它们是属于一个类别。所以点间的距离成为重要的判断参量。

同一类别中点间的距离一般来说比不同类别点间距离要小。一个点属于某一类，则该点到该类的中心距离要小于到其他类的中心距离。因此，在集群中心已确定的情况下，以每个点到这些类别中心的距离作为判定的准则，距离最小即为该点属于这一类，这样就可以完成分类工作。

这就是说，运用距离判别函数时，要求各个类别点群的中心位置已知。对于光谱特征空间中的任何一点K，计算它到各个中心点的距离，如果di＝min{dk，k＝1，2，…，N}，则该点属于第i类，而不属于其他类。

常用的距离有下面几种。

1.绝对距离

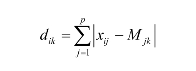
式中：dik为当前像素i到类k的距离；p为波段个数；xij为像素i在j波段的亮度值；Mjk为类k在波段j的数值。从上述公式可以看出，绝对距离公式使用数学中的绝对值概念，对各个波段进行绝对值求和，由于对各波段使用的权重系数都为1，因此也称为等混合距离。该公式比较简单，而且便于理解，在分类中经常使用。

2.欧氏距离

欧氏（Euclidean）距离是平面上两点之间的距离，应用也最广。(www.xing528.com)

欧氏距离中各特征参数也是等权的。在使用绝对距离和欧氏距离时，需要注意以下问题：

（1）特征参数需要进行标准化。

例如，若选择某个波段亮度值和某种波段亮度比值作为两个特征参数，此时就会出现问题。因为波段的亮度值通常是整数，而且都很大；而比值常为大于0小于1的小数，将这样两个数量级相差很大的参数以同等的权重组合起来，只能突出绝对值大的特征参数的作用，而绝对值小的特征参数基本不起作用。因此，为了克服这种毛病，在进行分类前要对数据进行标准化。

（2）特征参数间的相关性。

特征参数间通常是相关的。相关意味着特征参数在表征地物特征方面有共性。若特征参数中的大部分相关性较强，而个别的相关性不大，则一般来说相关的参数和不相关的参数在距离中的权重是不一样的，但在上述公式中权重都是1，是相同的。因此需要克服这一毛病，可以先将特征参数进行一定的线性变化，使它们之间成为线性无关，或者采用下面的马氏距离解决这个问题。

3.马氏距离

马氏距离（Mahalanobis）是一种加权的欧氏距离，它通过协方差矩阵来考虑变量的相关性。这是由于在实际中，各点群的形状可以看成大小和方向各不相同的椭球体，如图10-2所示。

图10-2　马氏距离

在图10-2中，尽管K点距A点集群的距离比距B点集群的距离要小，但由于B点群比A点群离散得多，因而把K点划入B类更合理。加权的权重与计算的距离与各点群的方差有关。方差越大，计算的距离就越短。如果各个点群具有相同的方差，则马氏距离是欧氏距离的平方。