Laplacian算子及其应用

比较上述梯度法，可知这些梯度法尽管所使用的模板不同，但本质都是线性一阶微分算子。下面介绍拉普拉斯算子。Laplacian算子是线性二阶微分算子，即。

对于离散的数字图像，二阶导数可以用二阶差分近似计算，Laplacian算子的表达式为：

∇2f (x,y）＝f (x+1,y )+f (x-1,y )+f (x,y+1)+f (x,y-1)-4f (x,y )

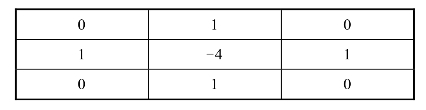
使用模板来表示，拉普拉斯算子相当于取某像素的上下左右4个相邻像素的值相加的和再减去该像素的4倍，作为该像素新的灰度值。

相应的模板可表示为

下面看看拉普拉斯算子的物理意义。想一想，梯度运算检测的是图像的空间灰度变化率，因此，图像上只要有灰度变化就有变化率，没有灰度变化，其变化率就为0。但Laplacian 算子检测的是变化率的变化率，即二阶微分。在图像上灰度均匀和变化均匀的部分，根据Laplacian 算子计算出的值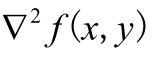都为0。因此，它检测的区域为灰度值发生不均匀变化的区域，或者灰度值突变的部分。

图8-9（a）是一幅7×7的数字图像，图像中存在边界。其左上部分的灰度变化均匀。以Laplacian算法对该图像进行锐化提取边缘的结果见图8-9（b），图像中灰度为常数的下部与变化均匀的左上部值均为0。在锐化结果中出现了负值，表示灰度值发生了增大趋势。但在计算机存储中，图像的灰度值不能为负数，因此解决的办法，就是对所有值加上一个正常数。(www.xing528.com)

另外一种处理办法是用原图像的值减去Laplacian算法的计算结果的整数倍，即

g( x,y）＝f (x,y )-k ∇2f (x,y )

上式中：k为正整数；f（x，y）为原图像；∇2f（x，y）为Laplacian计算结果；g（x，y）为最后计算结果。图8-9（c）是当k=1时的计算结果，相当于图像（a）减去图像（b）的结果。这样的处理结果既保留了原图像作为背景，又扩大了边缘处的对比度，锐化效果更好一些。

在使用中要注意的是，某些软件使用的模板的符号与上面的相反，需要用户仔细研究一番。除了上述算法外，Laplacian方法还有一些其他的算法，这里不详细介绍。

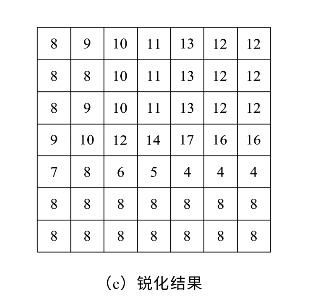
图8-9　Laplacian算法

另外，与其他梯度算子不同，拉普拉斯算子是各向同性的。拉普拉斯锐化效果容易受图像中的噪声的影响。因此，在实际应用中，经常先进行平滑滤波，然后才进行拉普拉斯锐化。考虑到各向同性的性质和平滑的特点，常选择高斯函数作为平滑滤波函数，即先进行高斯低通滤波。同时窗口大小的选择对拉普拉斯锐化也有明显的影响。因此，选择合适的窗口大小，并综合应用不同的处理方法，才能得到较好的锐化效果。