同态滤波(homo-morphic filter)是减少低频增加高频,从而减少光照变化并锐化边缘或细节的图像滤波方法。在数学算法上,同态滤波是在进行快速傅里叶变换之前先做一个对数运算。然后在IFFT之后,再做指数运算。注意,对数运算与指数运算是互为反的函数。其基本操作步骤如图7-8所示。
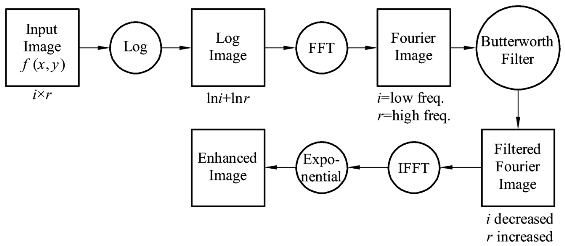
图7-8 同态滤波流程
为什么使用同态滤波呢?
因为一幅图像f(x,y)可以用照射分量和反射分量来模拟,即
f(x,y)=i(x,y)·r(x,y)
其中:i(x,y)为照射分量;r(x,y)为反射分量。图像的照射分量是光照条件、阴影等的函数,空间上变化缓慢。反射分量是目标物体的函数,常常引起突变,特别是在不同地物的连接处。这些特性使得可以将频率域的低频成分与照射分量相联系,将高频成分与反射分量相联系。这种联系尽管是近似的,但处理后的图像清晰度大幅提高,这对于图像的增强很有好处。
下面看看图7-8的流程。总共分5步:
(1)取对数。
lnf(x,y)=lni(x,y)+lnr(x,y)
对图像进行对数运算,使图像运算从乘法变为加法,物理含义是分开照射分量和反射分量。然后,可以在频率域进行图像的处理。
(2)对上述的结果进行傅里叶变换。(https://www.xing528.com)
F(u,v)=I(u,v)·R(u,ν)
(3)选取滤波器函数H(u,v)对F(u,v)进行滤波,得到:
G(x,y)=H(u,v)·F(u,v)=H(u,v)·I(u,v)×H(u,v)·R(u,v)
在这里,H(u,v)称为同态滤波函数,它可以分别作用于照射分量和反射分量上。同态滤波函数的类型和参数的选择对滤波的结果影响很大。
(4)应用傅里叶逆变换将滤波后的图像转换到空间域上,即:
hf(x,y)=hi(x,y)·hr(x,y)
(5)再对上式进行指数变换,即:
g(x,y)=exp|hf(x,y)|=exp|hi(x,y|·exp|hr(x,y)|
不同空间分辨率的遥感图像使用同态滤波的效果不同。如果图像中的光照是均匀的,那么进行同态滤波产生的效果不大。但是,如果光照明显是不均匀的,那么同态滤波有助于表现出图像中暗处的细节(图7-9)。

图7-9 同态滤波
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




