几何畸变有多种校正方法，可以根据卫星的参数进行图像的粗纠正。这里讲述的几何精纠正，也是最常用的一种精校正方法。它主要是使用地面控制点来进行几何畸变纠正。它的基本原理是回避成像的几何畸变过程，直接利用地面控制点数据对遥感图像的几何畸变本身进行数学纠正。无论遥感图像的畸变是挤压、扭曲、缩放还是偏移造成的，在控制点的控制作用下，控制点的几何位置都是正确的，控制点与控制点之间的图像是有变形的，但通过加密控制点，可以使它们之间的图像最大变形控制在要求范围之内。这样通过畸变的图像中的控制点与纠正后图像的控制点产生一一映射关系后，便可以产生一个适当的函数映射来映射其他点的像素信息。
通过上述原理，几何精纠正具体的实现过程如下：给定一函数模型（一般使用多项式模型，包括一次的，或者二次的），利用地面控制点数据的对应关系确定该函数模型的具体参数。这些参数一旦计算得到，也就确定了这个几何畸变的数学模型。这样也就建立了原始图像与标准图像的对应关系，然后利用这种对应关系，把畸变图像空间中的其他像素全部变换到标准图像中的像素，从而实现图像的几何精纠正。
6.2.2.1 几何精纠正的操作步骤
遥感图像几何精纠正的步骤如下所示，一般遥感软件也都开发了此功能：
（1）准备工作，包括图像数据、地形图、大地测量成果、航天器轨道参数和传感器姿态参数的收集与分析。如果图像为胶片，需通过扫描转为数字图像。
（2）输入原始数字图像。按规定的格式读取遥感数字图像。
（3）确定工作范围。根据工作要求，确定工作范围，然后对遥感图像进行剪裁，减少计算机运算量。
（4）选择地面控制点。根据图像特征和地区情况，结合野外调查和地形图选择地面控制点。控制点的测量可用全站仪、经纬仪和GPS。本步骤的测量精度直接影响图像最后的纠正精度。
（5）选择地图投影。根据工作要求，选择地图投影，确定相关的投影参数。
（6）匹配地面控制点和像素位置。地面控制点和相应的像素为同名地物点，应该清晰无误地进行匹配。
（7）评估纠正精度。在使用遥感软件进行几何精纠正的过程中，可以预测每个控制点可能产生的误差及总的平均误差。如果点的误差很大，一般来说需要增加控制点来提高精度。
（8）重采样。待纠正的数字图像本身属于规则的离散采样，非采样点上的灰度值需要通过采样点（已知像素）内插来获取，即重采样。重采样时，附近若干像素（采样点）的灰度值对被采样点影响的大小（权重）可以用重采样函数表达。重采样完成，就得到了纠正后的图像。
（9）输出纠正后图像。
6.2.2.2 地面控制点的选取
地面控制点（GCP，Ground Control Point）是几何纠正中用来建立纠正方程的基础，是最关键的数据。如果控制点选择不合适，就会产生较大的误差。几何精纠正中产生的问题，几乎都是由地面控制点选择不恰当造成的。
1.控制点数目和分布
控制点数目的最小值按未知系数多少来确定。对于常用的多项式方法而言，一阶多项式有6个参数，需要6个方程才能求解，而一个控制点就能提供两个方程，因此至少需要3个控制点。而二阶多项式有12个系数，需要12个方程（至少6个控制点）。三阶多项式至少需要10个控制点，但纠正效果不佳。因此在大多数几何精纠正中，一般使用一次、二次多项式进行纠正。
其次，实际工作经验表明，使用最少数目的控制点来校正图像效果也不好，误差较大，因此要加密控制点。一般来说，控制点个数的选取的数目最好大于最低数目的5倍，而且控制点在整个幅面能尽量地均匀分布。如果图像扭曲变形明显，那么更要强调这种分布的均匀性。在图像边缘处，在地面特征变化大的地区，如河流拐弯处等，没有控制点而靠计算推出对应点会产生较大的变形误差。因此，在条件允许的情况下，控制点要均匀地分布在工作地区。
2.图像中控制点的确定
首先应在图像上确定控制点。受图像空间分辨率的影响，控制点在图像上可能比较模糊。因此，在选择前需要对图像进行一些处理，如图像的锐化、降噪和彩色合成等，以进一步突出控制点信息。彩色合成方法中，真彩色合成产生的图像与人眼的视觉效果比较相近，有助于利用已有的知识进行分析判断，应该优先使用。
在图像上，控制点应该在容易分辨、相对稳定、特征明显的位置，如道路交叉点、河流弯曲或分汊处、海岸线弯曲处、湖泊边缘、飞机场跑道等。在变化不明显的大面积区域（如沙漠），控制点可以少一些。在特征变化大且对精度要求高的区域，应该多布点。但是，要尽可能避免控制点之间构成直线关系，避免控制点仅分布在狭长的范围里。
3.地面控制点坐标的确定
地面控制点的坐标可以通过地形图或现场实测获取。地形图年代与图像的年代应尽可能接近。受成像日期的影响，图像信息可能与实际地面信息差异较大。在这种情况下，如果没有可供参考的地形图，就需要根据现场情况对图像中初步确定的控制点进行调整。
大比例尺地形图可以提供精确的坐标信息，这是获取控制点地理坐标的主要数据来源。对于现势性要求比较高的数据，可以通过现场GPS测量获取控制点坐标。
目前，手持GPS的坐标精度在几米之内，可以用于TM图像的几何纠正。如果需要更高的纠正精度要求，可以通过差分GPS来获取坐标。使用GPS测量结果要注意投影问题。GPS 使用的是WGS84地心坐标系，可能与需要的坐标投影系统不同，在使用前要进行参数转换。
6.2.2.3 多项式纠正方程
常用的纠正方程有多项式和共线方程两种。共线方程方法严密，结果精确，缺点是计算复杂，且需要控制点具有高程值，一般在大比例尺制图、航空摄影中使用。
多项式纠正方程在实践中经常使用。该方法的原理直观、计算简单，特别是对地面相对平坦的图像，此时具有足够高的纠正精度。该方程对各种类型传感器的纠正具有普遍适用性，不仅可用于图像——地图的纠正，还常用于不同类型遥感图像之间的几何配准，以满足计算机分类、地物变化监测等处理的需要。
多项式纠正方法，最常用的是一次、二次多项式，三次以上的多项式在实际应用中用得比较少。对于简单的旋转、偏移和缩放变形，可以使用最基本的仿射变换公式进行纠正：
X＝ax+by+c
Y＝dx+ey+f(www.xing528.com)
通过上述公式，原图像上的点（x，y）映射成新图像上的点（X，Y）。各参数的取值，是通过控制点得到的。
更复杂一些的多项式纠正，用二次多项式纠正方程。二次多项式纠正方程如下：
X＝ax2+by2+cxy+dx+ey+f
Y＝gx2+hy2+ixy+jx+ky+l
上式中的参数与一次具有相同的含义，只是未知数增多。在使用多项式进行纠正时，应注意以下问题：
（1）多项式纠正的精度与地面控制点的精度、分布和数量及纠正的范围有关。地面控制点的精度越高、分布越均匀，数量越多，几何纠正的精度就越高。
（2）采用多项式纠正时，在地面控制点（GCP）处的拟合较好，但在其他点处的误差可能会较大。离GCP越远，误差越大。因此，图像的总体平均误差小并不能保证图像各点的误差都小。
（3）多项式次数的确定，取决于对图像中几何变形程度的认识，如果变形不复杂，那么一次多项式就可以满足要求了。理论上来说，次数越高，精度越大。但是在实际应用中，并非多项式的次数越高，纠正的精度越高。因此在实际应用中，提高纠正精度的方法，是加密控制点，并且让控制点尽量均匀分布，同时分区进行纠正。这些方法都非常有效。
为了克服控制点数据选择可能产生的问题，可用勒让德正交多项式代替一般多项式进行计算。此外Delaunay三角网通过对不规则的GCP进行三角网插值产生输出网格。如果多项式纠正结果的误差较大，且具有足够多的控制点，则可以考虑使用此方法。
6.2.2.4 重采样
重采样过程包括两步，像素位置变换和像素值的交换。纠正后的图像大小可以不同于原有的图像，没有数据的部分一般赋0值。
1.像素位置变换
像素位置变换是按选定的纠正方程把原始图像中的各个像素变换到输出图像相应的位置上去，变换方法分直接成图法和间接成图法。
1）直接成图法
直接成图法是纠正过程从原始图像出发，利用纠正方程将图像中的行列转换为新图像的行列，同时把原来行列中的灰度值写入新的图像对应的行列中。这种成图法在实际应用中应用得不多，使用得更多的是间接成图法。
2）间接成图法
间接成图法：以具有地理坐标的空白图像阵列为基础，根据纠正公式计算规则网的地理坐标（X，Y）在原始图像中对应的位置（x，y）；根据（x，y）与周围像素之间的关系内插产生新的像素值，然后把像素值写到（X，Y）中。
新像素并不对应整个旧像素，而是对应原图像中某几个像素的一些部分之和。此时需要对新像素进行内插处理。内插计算像素值的过程称为数字图像的重采样。因此间接成图法又称为灰度重采样方法。在遥感影像中，遇到的实际情况大多如此，因此在实践中经常采用这种方法。
2.图像重采样方法
常用的重采样方法有最近邻法、双线性内插法和三次卷积内插方法，其中，以最近邻法最简单，计算速度快。三次卷积法采样中的误差约为双线性内插的1/3，产生的图像比较平滑，但计算工作量大、耗费时间长。
1）最近邻重采样
如上所述，由于新像素并不对应整个旧像素，而是对应原图像中某几个像素的一些部分之和。一般来说，一个新像素包含原图像中的4个像素的部分之和。因此采用最近邻算法，首先找到新像素的位置（x，y），然后比较新像素的位置与原图像中4个像素位置的距离，选取原图像中那个最近的像素的灰度值作为新像素的灰度值。
最近邻重采样算法简单，最大优点是保持像素值不变。但是，纠正后的图像可能具有不连续性，会影响制图效果，当相邻像素的灰度值差异较大时，可能会产生较大的误差。
2）双线性内插重采样
双线性内插法是线性内插法在二维平面上的扩展。该方法在很多教科书上都有讲解，这里不再赘述。
该方法的好处在于简单，并且具有一定的精度，一般能得到满意的插值效果。其缺点是此方法具有低通滤波的性质，对图像起到平滑作用，会损失图像中的一些边缘或线性信息，导致图像模糊。
3）三次卷积内插重采样
理论上的最佳插值函数是辛克函数。辛克函数如下：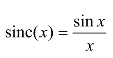
，但我们用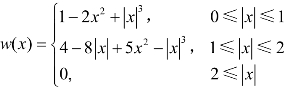
来逼近该函数。
三次卷积插值就是利用上述多项式逼近该函数的。三次卷积内插一般需要16个原始像素进行计算。该方法产生的图像比较平滑，缺点是计算量很大。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
